MATLAB - Differential
MATLAB liefert den diff Befehl zur Berechnung symbolischer Ableitungen. In seiner einfachsten Form übergeben Sie die zu unterscheidende Funktion als Argument an den Befehl diff.
Lassen Sie uns zum Beispiel die Ableitung der Funktion f(t) =3t 2 berechnen + 2t -2
Beispiel
Erstellen Sie eine Skriptdatei und geben Sie den folgenden Code ein −
syms t f = 3*t^2 + 2*t^(-2); diff(f)
Wenn der obige Code kompiliert und ausgeführt wird, erzeugt er das folgende Ergebnis −
ans = 6*t - 4/t^3
Das Folgende ist das Oktaväquivalent der obigen Berechnung −
pkg load symbolic
symbols
t = sym("t");
f = 3*t^2 + 2*t^(-2);
differentiate(f,t)
Octave führt den Code aus und gibt das folgende Ergebnis zurück −
ans = -(4.0)*t^(-3.0)+(6.0)*t
Überprüfung elementarer Differenzierungsregeln
Wir wollen kurz verschiedene Gleichungen oder Regeln zur Differentiation von Funktionen aufstellen und diese Regeln verifizieren. Zu diesem Zweck schreiben wir f'(x) für eine Ableitung erster Ordnung und f"(x) für eine Ableitung zweiter Ordnung.
Es folgen die Regeln für die Differenzierung −
Regel 1
Für alle Funktionen f und g und alle reellen Zahlen sind a und b die Ableitung der Funktion −
h(x) =af(x) + bg(x) bezüglich x ist gegeben durch −
h'(x) =af'(x) + bg'(x)
Regel 2
Die Summe und Subtraktion Regeln besagen, dass, wenn f und g zwei Funktionen sind, f' und g' jeweils ihre Ableitungen sind, dann
(f + g)' =f' + g'
(f - g)' =f' - g'
Regel 3
Das Produkt Die Regel besagt, dass wenn f und g zwei Funktionen sind, f' bzw. g' ihre Ableitungen sind, dann
(f.g)' =f'.g + g'.f
Regel 4
Der Quotient Die Regel besagt, dass wenn f und g zwei Funktionen sind, f' bzw. g' ihre Ableitungen sind, dann
(f/g)' =(f'.g - g'.f)/g 2
Regel 5
Das Polynom oder elementare Potenzregel besagt, dass gilt, wenn y =f(x) =x n , dann f' =n. x (n-1)
Ein direktes Ergebnis dieser Regel ist, dass die Ableitung jeder Konstanten Null ist, d. h. wenn y =k ist , jede Konstante, dann
f' =0
Regel 6
Die Kette Regel besagt, dass Ableitung der Funktion einer Funktion h(x) =f(g(x)) bezüglich x ist,
h'(x)=f'(g(x)).g'(x)
Beispiel
Erstellen Sie eine Skriptdatei und geben Sie den folgenden Code ein −
syms x syms t f = (x + 2)*(x^2 + 3) der1 = diff(f) f = (t^2 + 3)*(sqrt(t) + t^3) der2 = diff(f) f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2) der3 = diff(f) f = (2*x^2 + 3*x)/(x^3 + 1) der4 = diff(f) f = (x^2 + 1)^17 der5 = diff(f) f = (t^3 + 3* t^2 + 5*t -9)^(-6) der6 = diff(f)
Wenn Sie die Datei ausführen, zeigt MATLAB das folgende Ergebnis an −
f = (x^2 + 3)*(x + 2) der1 = 2*x*(x + 2) + x^2 + 3 f = (t^(1/2) + t^3)*(t^2 + 3) der2 = (t^2 + 3)*(3*t^2 + 1/(2*t^(1/2))) + 2*t*(t^(1/2) + t^3) f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2) der3 = (2*x - 2)*(3*x^3 - 5*x^2 + 2) - (- 9*x^2 + 10*x)*(x^2 - 2*x + 1) f = (2*x^2 + 3*x)/(x^3 + 1) der4 = (4*x + 3)/(x^3 + 1) - (3*x^2*(2*x^2 + 3*x))/(x^3 + 1)^2 f = (x^2 + 1)^17 der5 = 34*x*(x^2 + 1)^16 f = 1/(t^3 + 3*t^2 + 5*t - 9)^6 der6 = -(6*(3*t^2 + 6*t + 5))/(t^3 + 3*t^2 + 5*t - 9)^7
Das Folgende ist das Oktaväquivalent der obigen Berechnung −
pkg load symbolic
symbols
x = sym("x");
t = sym("t");
f = (x + 2)*(x^2 + 3)
der1 = differentiate(f,x)
f = (t^2 + 3)*(t^(1/2) + t^3)
der2 = differentiate(f,t)
f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2)
der3 = differentiate(f,x)
f = (2*x^2 + 3*x)/(x^3 + 1)
der4 = differentiate(f,x)
f = (x^2 + 1)^17
der5 = differentiate(f,x)
f = (t^3 + 3* t^2 + 5*t -9)^(-6)
der6 = differentiate(f,t)
Octave führt den Code aus und gibt das folgende Ergebnis zurück −
f = (2.0+x)*(3.0+x^(2.0)) der1 = 3.0+x^(2.0)+(2.0)*(2.0+x)*x f = (t^(3.0)+sqrt(t))*(3.0+t^(2.0)) der2 = (2.0)*(t^(3.0)+sqrt(t))*t+((3.0)*t^(2.0)+(0.5)*t^(-0.5))*(3.0+t^(2.0)) f = (1.0+x^(2.0)-(2.0)*x)*(2.0-(5.0)*x^(2.0)+(3.0)*x^(3.0)) der3 = (-2.0+(2.0)*x)*(2.0-(5.0)*x^(2.0)+(3.0)*x^(3.0))+((9.0)*x^(2.0)-(10.0)*x)*(1.0+x^(2.0)-(2.0)*x) f = (1.0+x^(3.0))^(-1)*((2.0)*x^(2.0)+(3.0)*x) der4 = (1.0+x^(3.0))^(-1)*(3.0+(4.0)*x)-(3.0)*(1.0+x^(3.0))^(-2)*x^(2.0)*((2.0)*x^(2.0)+(3.0)*x) f = (1.0+x^(2.0))^(17.0) der5 = (34.0)*(1.0+x^(2.0))^(16.0)*x f = (-9.0+(3.0)*t^(2.0)+t^(3.0)+(5.0)*t)^(-6.0) der6 = -(6.0)*(-9.0+(3.0)*t^(2.0)+t^(3.0)+(5.0)*t)^(-7.0)*(5.0+(3.0)*t^(2.0)+(6.0)*t)
Ableitungen von exponentiellen, logarithmischen und trigonometrischen Funktionen
Die folgende Tabelle enthält die Ableitungen häufig verwendeter exponentieller, logarithmischer und trigonometrischer Funktionen −
| Funktion | Ableitung |
|---|---|
| c a.x | c a.x .ln c.a (ln ist natürlicher Logarithmus) |
| e x | e x |
| lnx | 1/x |
| lnc x | 1/x.lnc |
| x x | x x .(1 + Inx) |
| sünde(x) | cos(x) |
| cos(x) | -sünde(x) |
| tan(x) | Sek. 2 (x) oder 1/cos 2 (x) oder 1 + tan 2 (x) |
| Kinderbett(x) | -csc 2 (x) oder -1/sin 2 (x) oder -(1 + Kinderbett 2 (x)) |
| sek(x) | sec(x).tan(x) |
| csc(x) | -csc(x).cot(x) |
Beispiel
Erstellen Sie eine Skriptdatei und geben Sie den folgenden Code ein −
syms x y = exp(x) diff(y) y = x^9 diff(y) y = sin(x) diff(y) y = tan(x) diff(y) y = cos(x) diff(y) y = log(x) diff(y) y = log10(x) diff(y) y = sin(x)^2 diff(y) y = cos(3*x^2 + 2*x + 1) diff(y) y = exp(x)/sin(x) diff(y)
Wenn Sie die Datei ausführen, zeigt MATLAB das folgende Ergebnis an −
y = exp(x) ans = exp(x) y = x^9 ans = 9*x^8 y = sin(x) ans = cos(x) y = tan(x) ans = tan(x)^2 + 1 y = cos(x) ans = -sin(x) y = log(x) ans = 1/x y = log(x)/log(10) ans = 1/(x*log(10)) y = sin(x)^2 ans = 2*cos(x)*sin(x) y = cos(3*x^2 + 2*x + 1) ans = -sin(3*x^2 + 2*x + 1)*(6*x + 2) y = exp(x)/sin(x) ans = exp(x)/sin(x) - (exp(x)*cos(x))/sin(x)^2
Das Folgende ist das Oktaväquivalent der obigen Berechnung −
pkg load symbolic
symbols
x = sym("x");
y = Exp(x)
differentiate(y,x)
y = x^9
differentiate(y,x)
y = Sin(x)
differentiate(y,x)
y = Tan(x)
differentiate(y,x)
y = Cos(x)
differentiate(y,x)
y = Log(x)
differentiate(y,x)
% symbolic packages does not have this support
%y = Log10(x)
%differentiate(y,x)
y = Sin(x)^2
differentiate(y,x)
y = Cos(3*x^2 + 2*x + 1)
differentiate(y,x)
y = Exp(x)/Sin(x)
differentiate(y,x)
Octave führt den Code aus und gibt das folgende Ergebnis zurück −
y = exp(x) ans = exp(x) y = x^(9.0) ans = (9.0)*x^(8.0) y = sin(x) ans = cos(x) y = tan(x) ans = 1+tan(x)^2 y = cos(x) ans = -sin(x) y = log(x) ans = x^(-1) y = sin(x)^(2.0) ans = (2.0)*sin(x)*cos(x) y = cos(1.0+(2.0)*x+(3.0)*x^(2.0)) ans = -(2.0+(6.0)*x)*sin(1.0+(2.0)*x+(3.0)*x^(2.0)) y = sin(x)^(-1)*exp(x) ans = sin(x)^(-1)*exp(x)-sin(x)^(-2)*cos(x)*exp(x)
Berechnung von Ableitungen höherer Ordnung
Um höhere Ableitungen einer Funktion f zu berechnen, verwenden wir die Syntax diff(f,n) .
Berechnen wir die zweite Ableitung der Funktion y =f(x) =x .e -3x
f = x*exp(-3*x); diff(f, 2)
MATLAB führt den Code aus und gibt das folgende Ergebnis zurück −
ans = 9*x*exp(-3*x) - 6*exp(-3*x)
Das Folgende ist das Oktaväquivalent der obigen Berechnung −
pkg load symbolic
symbols
x = sym("x");
f = x*Exp(-3*x);
differentiate(f, x, 2)
Octave führt den Code aus und gibt das folgende Ergebnis zurück −
ans = (9.0)*exp(-(3.0)*x)*x-(6.0)*exp(-(3.0)*x)
Beispiel
Lassen Sie uns in diesem Beispiel ein Problem lösen. Angenommen, eine Funktion y =f(x) =3 sin(x) + 7 cos(5x) . Wir müssen herausfinden, ob die Gleichung f" + f =-5cos(2x) ist gilt.
Erstellen Sie eine Skriptdatei und geben Sie den folgenden Code ein −
syms x
y = 3*sin(x)+7*cos(5*x); % defining the function
lhs = diff(y,2)+y; %evaluting the lhs of the equation
rhs = -5*cos(2*x); %rhs of the equation
if(isequal(lhs,rhs))
disp('Yes, the equation holds true');
else
disp('No, the equation does not hold true');
end
disp('Value of LHS is: '), disp(lhs);
Wenn Sie die Datei ausführen, zeigt sie das folgende Ergebnis an −
No, the equation does not hold true Value of LHS is: -168*cos(5*x)
Das Folgende ist das Oktaväquivalent der obigen Berechnung −
pkg load symbolic
symbols
x = sym("x");
y = 3*Sin(x)+7*Cos(5*x); % defining the function
lhs = differentiate(y, x, 2) + y; %evaluting the lhs of the equation
rhs = -5*Cos(2*x); %rhs of the equation
if(lhs == rhs)
disp('Yes, the equation holds true');
else
disp('No, the equation does not hold true');
end
disp('Value of LHS is: '), disp(lhs);
Octave führt den Code aus und gibt das folgende Ergebnis zurück −
No, the equation does not hold true Value of LHS is: -(168.0)*cos((5.0)*x)
Ermitteln der Maxima und Minima einer Kurve
Wenn wir nach den lokalen Maxima und Minima für einen Graphen suchen, suchen wir grundsätzlich nach den höchsten oder niedrigsten Punkten auf dem Graphen der Funktion an einem bestimmten Ort oder nach einem bestimmten Wertebereich der symbolischen Variablen.
Für eine Funktion y =f(x) werden die Punkte auf dem Graphen, an denen der Graph keine Steigung hat, als stationäre Punkte bezeichnet . Mit anderen Worten, stationäre Punkte sind dort, wo f'(x) =0.
Um die stationären Punkte einer Funktion zu finden, die wir differenzieren, müssen wir die Ableitung gleich Null setzen und die Gleichung lösen.
Beispiel
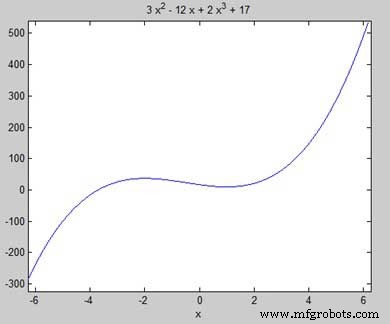
Lassen Sie uns die stationären Punkte der Funktion f(x) =2x 3 finden + 3x 2 − 12x + 17
Führen Sie die folgenden Schritte aus −
Lassen Sie uns zuerst die Funktion eingeben und ihren Graphen zeichnen.
syms x y = 2*x^3 + 3*x^2 - 12*x + 17; % defining the function ezplot(y)
MATLAB führt den Code aus und gibt den folgenden Plot zurück −
Hier ist der Octave-äquivalente Code für das obige Beispiel −
pkg load symbolic
symbols
x = sym('x');
y = inline("2*x^3 + 3*x^2 - 12*x + 17");
ezplot(y)
print -deps graph.eps
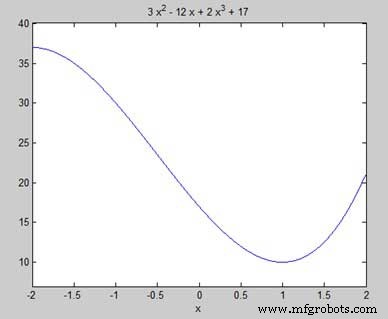
Unser Ziel ist es, einige lokale Maxima und Minima in der Grafik zu finden, also lassen Sie uns die lokalen Maxima und Minima für das Intervall [-2, 2] in der Grafik finden.
syms x y = 2*x^3 + 3*x^2 - 12*x + 17; % defining the function ezplot(y, [-2, 2])
MATLAB führt den Code aus und gibt den folgenden Plot zurück −
Hier ist der Octave-äquivalente Code für das obige Beispiel −
pkg load symbolic
symbols
x = sym('x');
y = inline("2*x^3 + 3*x^2 - 12*x + 17");
ezplot(y, [-2, 2])
print -deps graph.eps
Als nächstes berechnen wir die Ableitung.
g = diff(y)
MATLAB führt den Code aus und gibt das folgende Ergebnis zurück −
g = 6*x^2 + 6*x - 12
Hier ist das Oktaväquivalent der obigen Berechnung −
pkg load symbolic
symbols
x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)
Octave führt den Code aus und gibt das folgende Ergebnis zurück −
g = -12.0+(6.0)*x+(6.0)*x^(2.0)
Lassen Sie uns die Ableitungsfunktion g lösen, um die Werte zu erhalten, bei denen sie Null wird.
s = solve(g)
MATLAB führt den Code aus und gibt das folgende Ergebnis zurück −
s = 1 -2
Das Folgende ist das Oktaväquivalent der obigen Berechnung −
pkg load symbolic
symbols
x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)
roots([6, 6, -12])
Octave führt den Code aus und gibt das folgende Ergebnis zurück −
g = -12.0+(6.0)*x^(2.0)+(6.0)*x ans = -2 1
Das stimmt mit unserer Handlung überein. Bewerten wir also die Funktion f an den kritischen Punkten x =1, -2. Wir können einen Wert in einer symbolischen Funktion ersetzen, indem wir die subs verwenden Befehl.
subs(y, 1), subs(y, -2)
MATLAB führt den Code aus und gibt das folgende Ergebnis zurück −
ans = 10 ans = 37
Das Folgende ist das Oktaväquivalent der obigen Berechnung −
pkg load symbolic
symbols
x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)
roots([6, 6, -12])
subs(y, x, 1), subs(y, x, -2)
ans = 10.0 ans = 37.0-4.6734207789940138748E-18*I
Daher sind die Minimal- und Maximalwerte der Funktion f(x) =2x 3 + 3x 2 − 12x + 17, im Intervall [-2,2] sind 10 und 37.
Differentialgleichungen lösen
MATLAB stellt das dsolve zur Verfügung Befehl zum symbolischen Lösen von Differentialgleichungen.
Die einfachste Form von dsolve Befehl zum Finden der Lösung einer einzelnen Gleichung ist
dsolve('eqn')
wo eqn ist eine Textzeichenfolge, die zur Eingabe der Gleichung verwendet wird.
Es gibt eine symbolische Lösung mit einem Satz willkürlicher Konstanten zurück, die MATLAB als C1, C2 usw. bezeichnet.
Sie können auch Anfangs- und Randbedingungen für das Problem als kommagetrennte Liste nach der Gleichung als −
angeben
dsolve('eqn','cond1', 'cond2',…)
Zum Zwecke der Verwendung des dsolve-Befehls werden Ableitungen mit einem D gekennzeichnet . Beispielsweise wird eine Gleichung wie f'(t) =-2*f + cost(t) als −
eingegeben'Df =-2*f + cos(t)'
Höhere Ableitungen werden angezeigt, indem D in der Reihenfolge der Ableitung folgt.
Beispielsweise sollte die Gleichung f"(x) + 2f'(x) =5sin3x als −
eingegeben werden'D2y + 2Dy =5*sin(3*x)'
Nehmen wir ein einfaches Beispiel einer Differentialgleichung erster Ordnung:y' =5y.
s = dsolve('Dy = 5*y')
MATLAB führt den Code aus und gibt das folgende Ergebnis zurück −
s = C2*exp(5*t)
Nehmen wir ein weiteres Beispiel einer Differentialgleichung zweiter Ordnung:y" - y =0, y(0) =-1, y'(0) =2.
dsolve('D2y - y = 0','y(0) = -1','Dy(0) = 2')
MATLAB führt den Code aus und gibt das folgende Ergebnis zurück −
ans = exp(t)/2 - (3*exp(-t))/2
MATLAB



