Berechnung schneller Fourier-Transformationen auf der LPC55S69-MCU

Dieser Artikel untersucht die Transform Engine, einen weiteren Teil des PowerQuad, die es der MCU LPC55S69 ermöglicht, eine Fast Fourier Transform (FFT) zu berechnen.

Der Mikrocontroller LPC55S69 von NXP enthält viele Funktionen, die ihn für eine Vielzahl von Anwendungen geeignet machen. Die LPC55S69-MCU und ihre PowerQuad-Einheit enthalten einzigartige Komponenten – die Biquad- und die Transform-Engine –, die verwendet werden, um verschiedene Aufgaben zu erledigen, wobei die Haupt-CPU-Kerne für andere Dinge frei bleiben.

In einem früheren Artikel, Understanding Digital Filtering with Embedded Microcontrollers, wurden verschiedene weit verbreitete Methoden zum Filtern und Verarbeiten von Datenproben im Zeitbereich untersucht. Dafür wurde die Biquad-Engine der PowerQuad-Einheit des LPC55S69 verwendet.

Dieser Artikel untersucht die Transform Engine, einen weiteren Teil des PowerQuad, die es der MCU LPC55S69 ermöglicht, eine Fast Fourier Transform (FFT) zu berechnen.

Diskrete Fourier-Transformationen verstehen

Bei alltäglichen Messungen wie Längen und Temperaturen gibt es eine Reihe von Werkzeugen, um die Größe und Temperatur des jeweiligen Messobjekts zu bestimmen. Bei Zeitbereichssignalen ist die Wahl des Messwerkzeugs möglicherweise nicht so offensichtlich. Betrachten Sie das folgende Signalbeispiel in Abbildung 1.

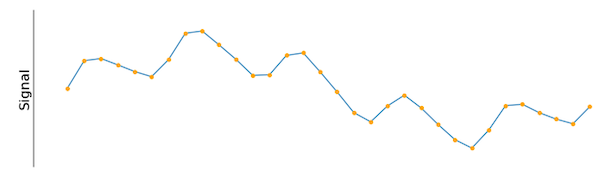
Abbildung 1. Ein in einem konstanten Intervall abgetastetes Eingangssignal.

Wie kann dieses Signal gemessen, verstanden und beschrieben werden? Mögliche Auswahlmöglichkeiten können die Amplitude, die Frequenz oder mehrere Werte sein, die mit Methoden aus der Statistik berechnet wurden. Eine Möglichkeit, um zu beginnen, besteht darin, das interessierende Signal gegen eine bekannte Kosinuswelle zu messen, wie in Abbildung 2 gezeigt.

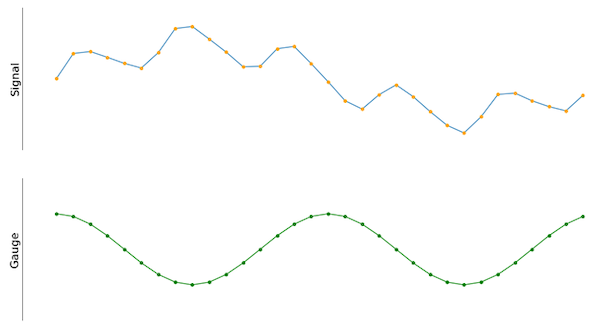
Abbildung 2. Das Eingangssignal neben einem Cosinus-Messsignal. Beide haben die gleiche Anzahl von Samples.

Da Amplitude und Frequenz der Kosinuswelle leicht festgelegt und somit identifiziert werden können, ist es möglich, die Kosinuswelle mit dem Eingangssignal zu vergleichen. Bei richtiger Ausführung quantifiziert der resultierende Wert des Skalarprodukts zwischen dem Eingangssignal und der Kosinuswelle, wie stark das Eingangssignal mit dem Messgerät korreliert. Aus diesem Grund ist es sinnvoll, sich das Eingangs- und das Messsignal als diskrete Eingangsarrays gleicher Länge vorzustellen, und es wird einfach, das Skalarprodukt zu berechnen.

Das Ergebnis ist ein Skalar, und seine Größe ist proportional dazu, wie gut das Eingangssignal mit dem Cosinus-Messsignal korreliert. Die Punktproduktoperation läuft auf viele Multiplikations- und Addieroperationen hinaus – dieselbe Operation, die unter Digitales Filtern mit eingebetteten Mikrocontrollern verstehen beschrieben wird.

Diese Methode führt schnell zu guten Ergebnissen. Es gibt jedoch einen speziellen Fall, der bei der Anwendung dieser Methode nicht funktioniert. Wenn das Eingangssignal eine Kosinuswelle mit derselben Frequenz wie das Messgerät ist, jedoch mit einer Phasenverschiebung von 90 Grad in Bezug auf das Messgerät, ist die Ausgabe des oben genannten Verfahrens null. Bei einer Sichtprüfung scheint es immer noch eine Korrelation zwischen dem Messgerät und dem Eingangssignal zu geben, aber es gibt Details, die wir berücksichtigen müssen.

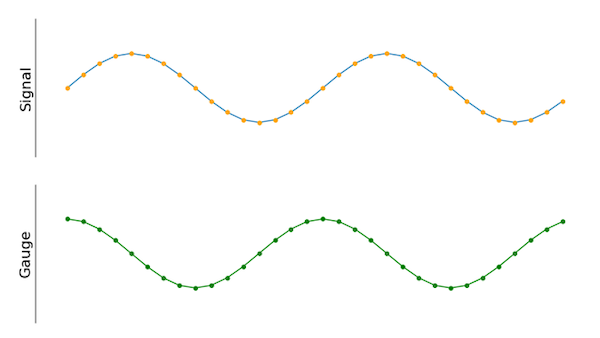
Abbildung 3. Das neue Messsignal ist im Vergleich zum alten um 90 Grad phasenverschoben.

Dieses Verhalten könnte mit der Messung der „Länge“ eines dünnen Papierstreifens verglichen werden. Wenn Sie ein Lineal verwenden, um die Länge einer Seite des Papierstreifens zu bestimmen, kann das Papier 25 cm lang und 2,5 cm breit sein. Beide Zahlen sind richtig, aber das Lineal musste um 90 Grad gedreht werden, um beide Maße zu erhalten. Beide Zahlen sind technisch korrekt und wir können sie zusammen verwenden, um eine wahre „Größe“ (Länge und Breite) unseres Blattes Papier zu erhalten. Um dieses Problem in Bezug auf unser Eingangssignal zu lösen, kann ein zweites Messgerät verwendet werden, wie in Abbildung 4 zu sehen.

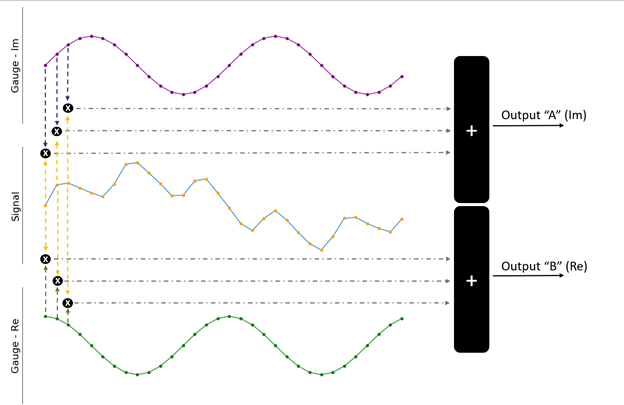
Abbildung 4. Beide Messsignale können verwendet werden, um das Eingangssignal besser zu quantifizieren.

Der einzige Unterschied zwischen den beiden Messgeräten (in Lila und Grün dargestellt) ist die 90-Grad-Phasenverschiebung. In der vorherigen Analogie entspricht dies dem Drehen des Lineals. Das Skalarprodukt wird zwischen dem Eingangssignal und jedem der Messgeräte berechnet, um die endgültige Ausgabe zu erhalten. Dies führt zu zwei Werten A und B, die jeweils angeben, wie gut die Eingabe mit einem der Messgeräte korreliert. Normalerweise werden sie als eine einzelne komplexe Zahl betrachtet:

Ausgabe =B + i * A

Der nächste Schritt besteht darin, das Eingangssignal mit einer Reihe von Messgeräten mit unterschiedlichen Frequenzen zu vergleichen (Abbildung 5).

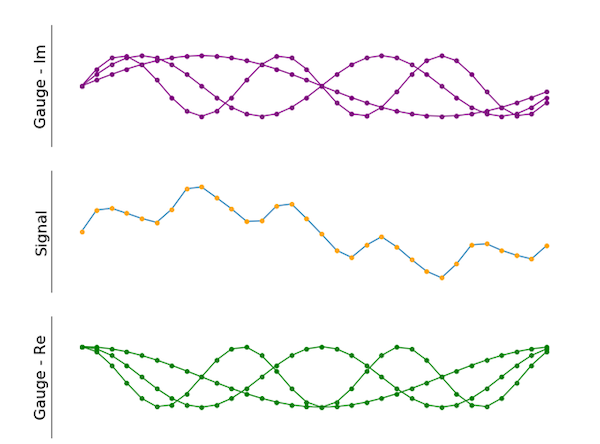
Abbildung 5. Es können auch mehrere Messgeräte angewendet werden. Die grünen sind im Vergleich zu den violetten um 90 Grad verschoben.

Wie das Bild zeigt, enthält das Endergebnis einige verschiedene Messgeräte. Der Imaginärteil (violett dargestellt) ist im Vergleich zu den grünen Signalen (realer Teil) um 90 Grad phasenverschoben, genau wie im oben gezeigten Beispiel mit zwei Spurweiten. Der Anzahl der verschiedenen Spurweiten sind keine Grenzen gesetzt.

Die Verwendung dieser Technik – die als diskrete Fourier-Transformation (DFT) bezeichnet wird – liefert die Erzeugung eines Spektrums von Ausgaben bei allen für ein Problem interessierenden Frequenzen. Mathematisch kann man die Technik wie folgt formulieren:

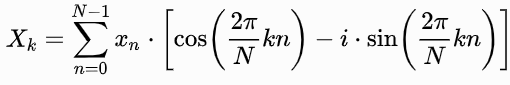
Gleichung 1. Die mathematische Beschreibung der DFT.

Dabei ist N die Anzahl der Abtastwerte im Eingangssignal und k die Frequenz der (Ko)sinus-Referenzmessgeräte.

Einschränkungen der schnellen Fourier-Transformation (FFT)

Die FFT ist eine numerisch effiziente Methode zum Berechnen der DFT, die im Vergleich zu dem oben diskutierten Verfahren weniger Multiplikations- und Addieroperationen erfordert. Bei der Eingabe gibt es jedoch einige Einschränkungen:

1. Die Länge der Eingabe muss eine Zweierpotenz sein.
2. Beliebige Eingabelängen und Frequenzabstände in der Ausgabe sind nicht zulässig. Die Ausgabe-Bins werden durch die Sample-Rate des Eingangssignals geteilt durch die Anzahl der Samples im Eingang beabstandet. Wenn der Eingang beispielsweise ein mit 48 kHz abgetastetes 256-Punkte-Signal ist, entsprechen die Ausgangsarrays Frequenzen im Abstand von 187 Hz (48.000 dividiert durch 256).
3. Wenn die Eingabe aus reellen Zahlen besteht (z. B. von einem ADC erhaltene Abtastwerte), ist die Ausgabe symmetrisch. Wenn die Eingabe beispielsweise aus 64 Abtastwerten besteht, besteht das FFT-Ergebnis auch aus 64 komplexen Zahlen. Die zweite Hälfte des Ausgabearrays enthält jedoch die komplex Konjugierten der ersten Hälfte.

Verwenden der PowerQuad-FFT-Engine

Die Mathematik hinter DFT/FFT-Operationen kann durch einfache Multiplikations- und Addieroperationen durchgeführt werden, was ideal für die Auslagerung der mathematischen Operationen an einen dedizierten Coprozessor wie das PowerQuad auf der LPC55S69-MCU ist. Aus diesem Grund können die Haupt-CPU-Kerne an anderen Aufgaben arbeiten.

Die Verwendung der PowerQuad FFT-Engine ist ein einfacher Vorgang, und das offizielle SDK enthält Beispielprojekte, die die Coprocessing-Funktionen demonstrieren. Ein spezielles Beispiel namens powerquad_transform demonstriert den FFT-Berechnungsprozess.

Die Datei powerquad_transform.c enthält mehrere Funktionen, die die verschiedenen FFT-Engine-Modi testen. Eine davon ist die Funktion PQ_RFFTFixed16Example. In diesem Beispiel wird das PowerQuad so initialisiert, dass es 16-Bit-Ganzzahldaten akzeptiert. Gleitkommadaten müssen vorher in Festkommawerte umgewandelt werden, da die PowerQuad-Transformations-Engine nur Ganzzahlen unterstützt.

FILTER_INPUT_LEN definiert die Anzahl der Eingabesamples. Das Ausgabearray hat die doppelte Länge, da es die Real- und Imaginärteile der resultierenden Werte speichern muss.

Abbildung 6. Dieser Teil des Codes definiert die Testdaten und die erwarteten Ergebnisse.

Das letzte Array enthält Testdaten zur Überprüfung des Ergebnisses. Beachten Sie, dass die zweite Hälfte des Arrays wie oben erwähnt die komplexen Konjugate enthält. Außerdem sind die Konjugate nicht gleich (z. B. das Paar 76,-50 und 77,49). Wie auch immer, sobald die Daten initialisiert wurden, wird die folgende Datenstruktur verwendet, um das PowerQuad zu konfigurieren:

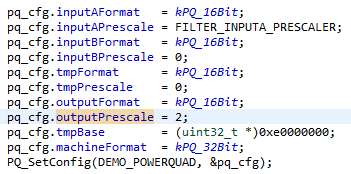
Abbildung 7. Dieser Teil des Beispielprogramms konfiguriert und initialisiert die PowerQuad-Einheit.

Es ist notwendig, die Eingabe herunterzuskalieren, um zu verhindern, dass der Algorithmus überläuft. Dieser Vorgang findet in der zweiten Zeile im obigen Bild statt. FILTER_INPUTA_PRESCALER wird auf fünf gesetzt, weil es 32 (zwei hoch fünf) Abtastwerte gibt. Die Vorskalierung ist ein weiteres Hardware-Feature des PowerQuad und wahrscheinlich der Grund für die Ungenauigkeit der erwarteten Testergebnisse.

Sobald alles eingerichtet ist, wird die Lage der Ein- und Ausgabebereiche an die PowerQuad-Einheit übergeben, was in der Funktion PQ_transformRFFT geschieht. Diese Methode setzt einige Konfigurationsregister und startet das PowerQuad durch Schreiben in das Steuerregister. In diesem Beispiel wartet die CPU, bis das PowerQuad fertig ist. Warten ist nicht immer erforderlich, und das PowerQuad kann Berechnungen asynchron ausführen, während die CPU andere Aufgaben ausführt.

Verwenden Sie PowerQuad für mathematische Operationen

Der PowerQuad ist ein Coprozessor für komplexe mathematische Operationen, der auf verschiedenen Geräten der LPC5500 MCU-Serie verfügbar ist. Es enthält eine spezielle Engine zur effizienten Berechnung von FFTs, die unabhängig von den Haupt-CPU-Kernen durchgeführt werden kann. Das SDK für die LPC55S69-MCU enthält Beispiele für die Einrichtung und Verwendung des PowerQuad.

Die Community-Seite von NXP enthält umfassende Informationen, Diskussionen und Artikel rund um die LPC55S69-MCU.

Branchenartikel sind eine Inhaltsform, die es Branchenpartnern ermöglicht, nützliche Nachrichten, Nachrichten und Technologien mit All About Circuits-Lesern auf eine Weise zu teilen, für die redaktionelle Inhalte nicht gut geeignet sind. Alle Branchenartikel unterliegen strengen redaktionellen Richtlinien, um den Lesern nützliche Neuigkeiten, technisches Know-how oder Geschichten zu bieten. Die in Branchenartikeln zum Ausdruck gebrachten Standpunkte und Meinungen sind die des Partners und nicht unbedingt die von All About Circuits oder seinen Autoren.