Beschreibung von kombinatorischen Schaltungen in Verilog

06. Januar 2019 von Dr. Steve Arar

In diesem Artikel werden die Techniken zur Beschreibung kombinatorischer Schaltungen in Verilog vorgestellt, indem untersucht wird, wie der bedingte Operator zur Beschreibung kombinatorischer Wahrheitstabellen verwendet wird.

In diesem Artikel werden die Techniken zum Beschreiben kombinatorischer Schaltungen in Verilog vorgestellt, indem untersucht wird, wie der Bedingungsoperator verwendet wird, um kombinatorische Wahrheitstabellen zu beschreiben. Es zeigt auch, wie man den „Immer“-Block von Verilog zum Beschreiben von kombinatorischen Schaltungen verwendet – ein „Immer“-Block kann uns eine noch einfachere Lösung bieten, um eine digitale Schaltung zu beschreiben.

In einem früheren Artikel haben wir die Verwendung des Verilog-Schlüsselworts „assign“ zum Ausführen einer fortlaufenden Zuweisung erörtert. Solche Zuweisungen sind immer aktiv und können verwendet werden, um eine Beschreibung von digitalen Schaltungen auf Gate-Ebene zu erhalten. Im folgenden Code, der beispielsweise ein UND-Gatter beschreibt, wird die rechte Seite kontinuierlich ausgewertet und das Ergebnis in das out1-Netz gestellt:

assign out1 =a &b;  

Verilog hat einen Bedingungsoperator (?:), der es uns ermöglicht, eine Bedingung zu überprüfen, bevor solche Zuweisungen vorgenommen werden. Die Syntax ist unten angegeben:

assign [signal_name] =[conditional_expression] ? [value_if_true] :[value_if_false]; 

Der „conditional_expression“ wird ausgewertet. Wenn es wahr ist, wird „value_if_true“ dem „signal_name“ zugewiesen. Wenn es nicht wahr ist, erhält "signal_name" "value_if_false". Betrachten Sie als Beispiel den folgenden Code:

assign out1 =(sel) ? (a &b) :(a|b); 

Wenn „sel“ wahr ist, wird a&b „out1“ zugewiesen. Wenn es nicht wahr ist, erhält "out1" a|b. Daher implementiert der obige Code die Funktionalität eines 2-zu-1-Multiplexers. Die konzeptionelle Implementierung dieses Codes kann wie in Abbildung 1 unten gezeigt aussehen.

Die bedingte Zuweisung ermöglicht uns eine abstraktere Beschreibung bestimmter Schaltungen, da sie die Funktionalität einer „if“-Anweisung hat, die in traditionellen Computerprogrammiersprachen zu finden ist. Der Bedingungsoperator kann in verschachtelter Form verwendet werden, um komplexere Schaltungen zu implementieren. Beispiel 1 erläutert diese Details.

Beispiel 1:Verschachtelte Bedingungsoperatoren

Verwenden Sie den Bedingungsoperator (?:), um einen 4-zu-2-Prioritätscodierer mit der folgenden Wahrheitstabelle zu beschreiben:

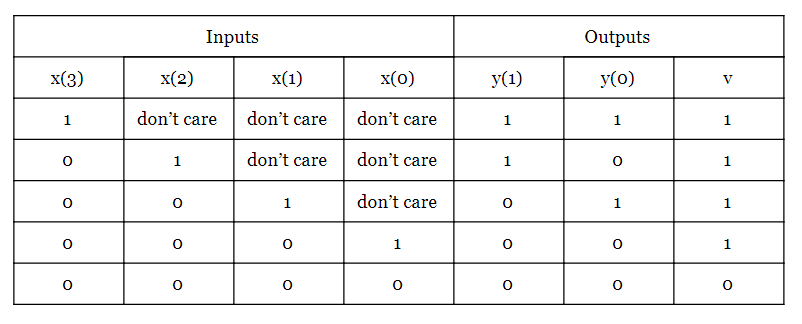
Der Verilog-Code für diesen Prioritätscodierer ist unten angegeben:

 Modul Prio_4_to_2 ( Eingangsleitung [3:0] x, Ausgangsleitung [1:0] y, Ausgangsleitung v ); weise y =x[3] zu? 2'b11 :x[2] ? 2'b10 :x[1] ? 2'b01 :2'b00; zuweisen v =( x[3] | x[2] | x[1] | x[0] ) ? 1'b1 :1'b0; Endmodul 

Abgesehen von den Zeilen 7 bis 10 enthält der Code die grundlegenden Sprachelemente, die in unserem vorherigen Artikel besprochen wurden. Werfen wir also einen Blick auf diese Zeilen.

Die Begriffe 2’b11, 2’b10, 2’b01 beziehen sich auf die Verilog-Notationen, die Zwei-Bit-Binärzahlen darstellen. Im Allgemeinen gibt die erste Zahl (vor ‘b) die Anzahl der Bits an. Der Buchstabe b gibt an, dass die Zahlen binär sind. Die Ziffern nach ‘b geben den Wert der Zahl an. Daher ist 2’b01 die Verilog-Notation, um eine Zwei-Bit-Binärzahl mit dem Wert 01 darzustellen, und 3’b100 bezeichnet eine Drei-Bit-Binärzahl mit dem Wert 100.

Zeile 7 überprüft das MSB der Eingabe x[3] in einem bedingten Operator. Wenn x[3]=1 ist, wird die Bedingung als wahr bewertet und 2’b11 wird y zugewiesen (der zugewiesene Wert wird aus der Wahrheitstabelle entnommen). Bei x[3]=0 wird die Bedingung als falsch ausgewertet und der Ausdruck nach dem Doppelpunkt (:) wird y zugewiesen. Der Ausdruck nach dem Doppelpunkt ist der Code in Zeile 8, der selbst ein weiterer bedingter Operator ist.

Der zweite Bedingungsoperator in Zeile 8 untersucht das zweithöchste Bit der Eingabe, x[2], um zu bestimmen, ob 2'b10 y zugewiesen werden sollte oder der Ausdruck nach dem Doppelpunkt, der wiederum ein weiterer Bedingungsoperator (Zeile 9) ist, bewerted werden. Sie können überprüfen, ob die y zugewiesenen Werte mit der angegebenen Wahrheitstabelle übereinstimmen.

Der gültige Ausgang (v) der Wahrheitstabelle ist logisch hoch, wenn mindestens ein Bit des Eingangs logisch hoch ist. Zeile 11 zeigt diese Beschreibung, indem der bitweise ODER-Operator (|) auf die Bits der Eingabe angewendet wird. Eine Xilinx ISE-Simulation des obigen Codes ist in Abbildung 2 dargestellt.

Abbildung 2. Eine Xilinx ISE-Simulation aus dem obigen Code.

Es ist wichtig zu beachten, dass die bedingten Ausdrücke nacheinander ausgewertet werden, bis ein wahrer Ausdruck gefunden wird. Die diesem wahren Ausdruck entsprechende Zuweisung wird ausgeführt. Dadurch haben die früher ausgewerteten Ausdrücke eine höhere Priorität im Vergleich zu den nächsten. Dies bedeutet, dass ein bedingter Operator theoretisch eher geeignet ist, ein Prioritätsnetzwerk (Abbildung 3) als eine symmetrische Struktur wie einen Multiplexer (Abbildung 4) zu implementieren.

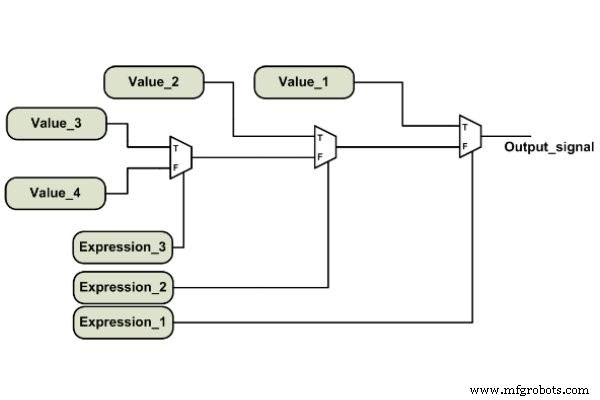
Abbildung 3. Ein vorrangiges Netzwerk.

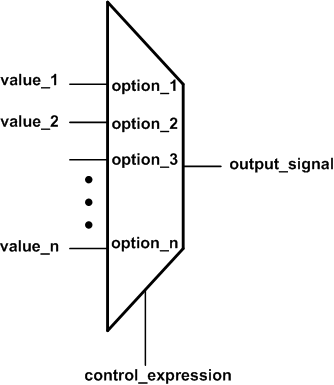
Abbildung 4. Ein n-zu-1-Multiplexer, bei dem es keine Priorität zwischen den Eingängen gibt.

Ein früherer Artikel enthüllt eine ähnliche Diskussion über gleichzeitige VHDL-Zuweisungen.

Verfahrensanweisungen von Verilog

Wir können jede kombinatorische Schaltung in einige grundlegende Logikgatter (UND, ODER, NICHT usw.) zerlegen und die Anweisung „assign“ verwenden, um diese Gatter zu beschreiben (eine Beschreibung auf Gatterebene). Wir können auch den im vorherigen Abschnitt diskutierten Bedingungsoperator verwenden, um eine abstraktere Art der Beschreibung einiger kombinatorischer Schaltungen zu haben (ähnlich der „if“-Anweisung von Computerprogrammiersprachen). Es gibt jedoch noch eine leistungsfähigere Lösung:den „Immer“-Block von Verilog zu verwenden.

Innerhalb eines „always“-Blocks können wir prozedurale Anweisungen haben, die nacheinander ausgeführt werden. Darüber hinaus unterstützt der „always“-Block abstrakte Sprachkonstrukte wie „if“- und „case“-Anweisungen.

Die Funktion der sequentiellen Ausführung zusammen mit den abstrakten Sprachkonstrukten, die in einem „Always“-Block verfügbar sind, ermöglicht es uns, die Funktionalität einer Schaltung einfacher zu beschreiben, da menschliches Denken sequentiell ist und auf abstrakten Beschreibungen beruht. Wir denken normalerweise in einer algorithmischen High-Level-Mode und nicht in Begriffen von Low-Level-Logikgattern. Ein „Immer“-Block kann uns eine einfachere Lösung bieten, um eine digitale Schaltung zu beschreiben. Weitere Informationen dazu, warum HDLs Beschreibungen basierend auf sequenziellen Anweisungen unterstützen, finden Sie in meinem Artikel Einführung in sequenzielle VHDL-Anweisungen.

Beispiel 2:"Immer" Blockanweisungen

Die vereinfachte Syntax eines „Immer“-Blocks ist unten angegeben:

immer @(sensitivity_list) begin sequentielle_Anweisungen; Ende 

Die sensitive_list gibt an, wann die sequentiellen Anweisungen innerhalb des „always“-Blocks ausgeführt werden sollen. Ziehen Sie beispielsweise in Betracht, den „immer“-Block zu verwenden, um die Schaltung in Abbildung 5 zu beschreiben.

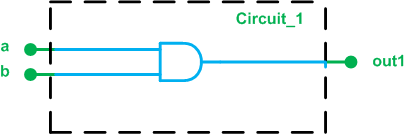
Abbildung 5. Circuit_1

Wenn sich entweder a oder b ändert, kann sich die Ausgabe ändern, was bedeutet, dass sowohl a als auch b in der Empfindlichkeitsliste des „always“-Blocks enthalten sein sollten. Im Allgemeinen sollten bei einer kombinatorischen Schaltung alle Eingangssignale in die Empfindlichkeitsliste aufgenommen werden.

Jetzt können wir den bitweisen AND-Operator verwenden, um die Funktionalität der Schaltung (a&b) zu beschreiben und das Ergebnis dem Ausgang zuzuweisen. Innerhalb eines „Immer“-Blocks gibt es zwei verschiedene Arten von Zuweisungen:die blockierende Zuweisung (=) und die nicht blockierende Zuweisung (<=). Mit der Sperrzuweisung erhalten wir folgenden Code:

immer @(a, b)begin out1 =a &b;end 

Was ist der Unterschied zwischen einer blockierenden Zuweisung und einer nicht blockierenden Zuweisung?

Bei einer blockierenden Zuweisung wird die rechte Seite ausgewertet und sofort out1 zugewiesen. Wenn Zeile 3 ausgeführt wird, wird out1 sofort aktualisiert, bevor wir zur nächsten Codezeile gehen. Der Name „Blockierungszuordnung“ betont, dass die kommenden Zeilen gesperrt werden, bis die linke Seite aktualisiert wird.

Bei einer nicht blockierenden Zuweisung wird der rechte Ausdruck ausgewertet, aber erst am Ende des „always“-Blocks auf die linke Variable angewendet. Die Wahl zwischen blockierender oder nicht blockierender Zuordnung kann für einen Anfänger verwirrend sein und eine unsachgemäße Verwendung kann zu einer unerwünschten Funktionalität führen. Zum Beispiel kann die Verwendung von Blockierungszuweisungen zum Ableiten von Flip-Flops eine Race-Condition einführen.

In diesem Einführungsartikel gehen wir nicht weiter ins Detail und halten uns nur an eine einfache Richtlinie, um potenzielle Fallstricke zu vermeiden:Verwenden Sie die blockierenden Zuweisungen beim Schreiben des Codes für eine kombinatorische Schaltung. Daher wird der „immer“-Block in Listing 1 verwendet, um ein UND-Gatter zu beschreiben.

In einem früheren Artikel haben wir uns mit dem Datentyp „wire“ von Verilog vertraut gemacht. Dieser Datentyp repräsentiert einen physikalischen Draht in unserem FPGA-Design. Innerhalb eines „Immer“-Blocks erlaubt uns der Verilog-Standard nicht, einem „Draht“ einen Wert zuzuweisen. Stattdessen verwenden wir den Datentyp „reg“. Der Name „reg“ ist etwas verwirrend, aber beachten Sie, dass ein „reg“ zu einem physischen Speicherelement in Ihrem Design führen kann oder nicht. Der folgende Code ist die Verilog-Beschreibung von Abbildung 5, die einen „Immer“-Block verwendet. Beachten Sie, dass der Ausgabedatentyp „reg“ sein sollte, da er seinen Wert von einer prozeduralen Zuweisung erhält.

 Modul Circuit_1 (Eingangsdraht a, Eingangsdraht b, Ausgangsreg. out1); immer @ (a, b) begin out1 =a &b; endmodul 

In diesem Artikel haben wir uns mit dem Bedingungsoperator von Verilog vertraut gemacht. Wir haben die verschachtelte Form dieses Operators verwendet, um einen Prioritätscodierer zu beschreiben. Dann haben wir ein mächtigeres Sprachkonstrukt berührt, den „Immer“-Block, um kombinatorische Schaltkreise zu beschreiben. In zukünftigen Artikeln werden wir die Verwendung des „always“-Blocks untersuchen, um sequentielle Schaltungen zu implementieren.