Schaltungseffekte

Das Prinzip nicht-sinusförmiger, sich wiederholender Wellenformen, die einer Reihe von Sinuswellen mit unterschiedlichen Frequenzen entsprechen, ist eine grundlegende Eigenschaft von Wellen im Allgemeinen und hat große praktische Bedeutung für das Studium von Wechselstromkreisen.

Das bedeutet, dass jedes Mal, wenn wir eine Wellenform haben, die nicht perfekt sinusförmig ist, die fragliche Schaltung so reagiert, als ob ihr eine Reihe von Spannungen unterschiedlicher Frequenz gleichzeitig auferlegt würden.

Wenn ein Wechselstromkreis einer Quellenspannung ausgesetzt wird, die aus einer Mischung von Frequenzen besteht, reagieren die Komponenten in diesem Kreis auf jede einzelne Frequenz auf unterschiedliche Weise. Jede reaktive Komponente wie ein Kondensator oder eine Induktivität stellt gleichzeitig eine einzigartige Impedanz für jede einzelne in einem Stromkreis vorhandene Frequenz dar.

Glücklicherweise wird die Analyse solcher Schaltungen relativ einfach durch die Anwendung des Superpositionssatzes , wobei die Mehrfrequenzquelle als eine Reihe von in Reihe geschalteten Einfrequenzspannungsquellen betrachtet wird und die Schaltung jeweils für eine Quelle analysiert wird, wobei die Ergebnisse am Ende summiert werden, um die Gesamtsumme zu bestimmen:

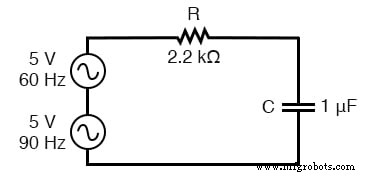
Schaltung durch eine Kombination von Frequenzen:60 Hz und 90 Hz

Analyseschaltung für 60-Hz-Quelle allein:

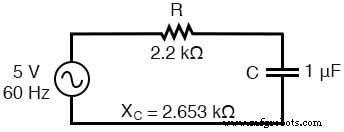
Schaltung zum Lösen von 60 Hz

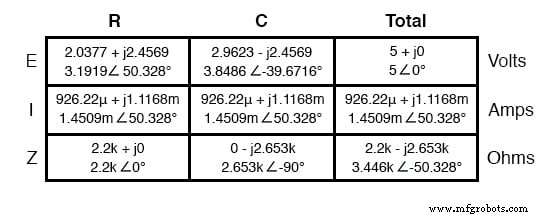
Analyse der Schaltung nur für eine 90-Hz-Quelle:

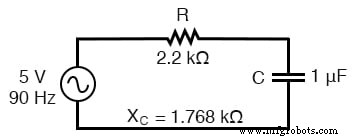
Kreis zum Lösen von 90 Hz

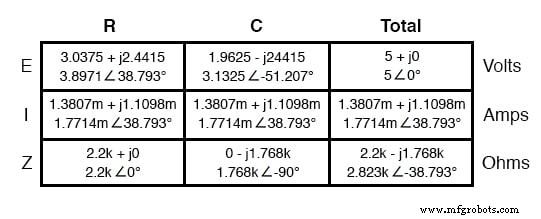
Überlagern wir die Spannungsabfälle über R und C, erhalten wir:

Da die beiden Spannungen an jeder Komponente unterschiedliche Frequenzen haben, können wir sie nicht zu einer einzigen Spannungszahl zusammenfassen, wie wir es könnten, wenn wir zwei Spannungen unterschiedlicher Amplitude und/oder Phasenwinkel bei derselben Frequenz addieren würden.

Die Notation komplexer Zahlen gibt uns die Möglichkeit, die Amplitude der Wellenform (Polargröße) und den Phasenwinkel (Polarwinkel) darzustellen, aber nicht die Frequenz.

Was wir aus dieser Anwendung des Überlagerungssatzes erkennen können, ist, dass am Kondensator eine Spannung von 60 Hz größer als eine Spannung von 90 Hz abfällt. Genau das Gegenteil gilt für den Spannungsabfall des Widerstands.

Dies ist erwähnenswert, insbesondere angesichts der Tatsache, dass die beiden Quellenspannungen gleich sind. Es ist diese Art von ungleicher Schaltungsantwort auf Signale unterschiedlicher Frequenz, auf die wir uns im nächsten Kapitel besonders konzentrieren werden.

Wir können das Superpositionstheorem auch auf die Analyse einer Schaltung anwenden, die von einer nicht sinusförmigen Spannung gespeist wird, beispielsweise einer Rechteckwelle. Wenn wir die Fourier-Reihe (mehrfaches Sinus-/Kosinus-Äquivalent) dieser Welle kennen, können wir sie als von einer in Reihe geschalteten Reihe mehrerer sinusförmiger Spannungsquellen mit den entsprechenden Amplituden, Frequenzen und Phasenverschiebungen stammend betrachten.

Unnötig zu erwähnen, dass dies für einige Wellenformen eine mühsame Aufgabe sein kann (eine genaue Rechteckwellen-Fourier-Reihe gilt als bis zur neunten Harmonischen oder insgesamt fünf Sinuswellen ausgedrückt!), aber es ist möglich. Ich erwähne dies nicht, um Sie zu erschrecken, sondern um Sie über die potenzielle Komplexität zu informieren, die hinter scheinbar einfachen Wellenformen lauert.

Eine echte Schaltung reagiert genauso auf eine Rechteckwelle wie auf eine unendliche Reihe von Sinuswellen mit ungeradzahligen Frequenzen und abnehmenden Amplituden.

Es ist bekannt, dass dies zu unerwarteten Schaltkreisresonanzen, Überhitzung des Transformator- und Induktorkerns aufgrund von Wirbelströmen, elektromagnetischem Rauschen über breite Bereiche des Frequenzspektrums und dergleichen führt. Techniker und Ingenieure müssen auf die möglichen Auswirkungen von nicht-sinusförmigen Wellenformen in Blindschaltkreisen aufmerksam gemacht werden.

Es ist bekannt, dass Oberwellen ihre Auswirkungen auch in Form von elektromagnetischer Strahlung zeigen.

Es wurden Studien zu den potenziellen Gefahren bei der Verwendung tragbarer Computer an Bord von Passagierflugzeugen durchgeführt, wobei die Tatsache zitiert wurde, dass hochfrequente Rechteckwellen-„Uhr“-Spannungssignale von Computern in der Lage sind, Funkwellen zu erzeugen, die den Betrieb der elektronischen Navigationsausrüstung des Flugzeugs stören könnten .

Es ist schon schlimm genug, dass typische Taktsignalfrequenzen von Mikroprozessoren im Bereich der Funkfrequenzbänder von Flugzeugen liegen, aber noch schlimmer ist die Tatsache, dass die harmonischen Vielfachen dieser Grundfrequenzen aufgrund der Tatsache, dass die Taktsignalspannungen quadratisch sind, einen noch größeren Bereich umfassen. wellenförmig und nicht sinusförmig.

Elektromagnetische „Emissionen“ dieser Art können auch in industriellen Anwendungen ein Problem darstellen, da Oberwellen aufgrund der (nichtlinearen) elektronischen Steuerung der Motor- und Elektroofenleistung in sehr großen Mengen vorkommen.

Die Grundfrequenz der Netzleitung kann nur 60 Hz betragen, aber diese harmonischen Frequenzvielfachen erstrecken sich theoretisch in unendlich hohe Frequenzbereiche. Niederfrequente Netzspannungen und -ströme strahlen nicht so gut in den Weltraum ab als elektromagnetische Energie, aber hohe Frequenzen schon.

Außerdem ist die kapazitive und induktive „Kopplung“, die durch nahe Leiter verursacht wird, bei hohen Frequenzen normalerweise stärker. Signalverkabelung in der Nähe von Stromkabeln neigt dazu, harmonische Interferenzen von den Stromkabeln weitaus stärker „aufzufangen“ als reine Sinuswellen-Interferenzen.

Dieses Problem kann sich in der Industrie manifestieren, wenn alte Motorsteuerungen durch neue elektronische Festkörper-Motorsteuerungen ersetzt werden, die eine höhere Energieeffizienz bieten.

Plötzlich kann es zu seltsamen elektrischen Störungen kommen, die auf Signalleitungen eingeprägt werden, die nie da waren, weil die alten Steuerungen nie Oberwellen erzeugten und diese hochfrequenten harmonischen Spannungen und Ströme dazu neigen, sich besser als alle anderen induktiv und kapazitiv an nahe gelegene Leiter zu „koppeln“. 60 Hz Signale von den alten Steuerungen verwendet.

RÜCKBLICK:

• Jede regelmäßige (sich wiederholende), nicht-sinusförmige Wellenform entspricht einer bestimmten Reihe von Sinus-/Cosinuswellen unterschiedlicher Frequenzen, Phasen und Amplituden plus einer DC-Offsetspannung, falls erforderlich. Der mathematische Prozess zur Bestimmung des Sinuswellenform-Äquivalents für jede Wellenform wird als Fourier-Analyse bezeichnet .
• Mehrfrequenz-Spannungsquellen können zur Analyse simuliert werden, indem mehrere Gleichfrequenz-Spannungsquellen in Reihe geschaltet werden. Die Analyse von Spannungen und Strömen erfolgt unter Verwendung des Überlagerungssatzes. HINWEIS:überlagerte Spannungen und Ströme unterschiedlicher Frequenzen können nicht in Form komplexer Zahlen addiert werden, da komplexe Zahlen nur Amplitude und Phasenverschiebung berücksichtigen, nicht die Frequenz!
• Oberschwingungen können Probleme verursachen, indem sie ungewollte („rauschende“) Spannungssignale auf nahegelegene Stromkreise einprägen. Diese unerwünschten Signale können durch kapazitive Kopplung, induktive Kopplung, elektromagnetische Strahlung oder eine Kombination daraus entstehen.

VERWANDTE ARBEITSBLÄTTER:

• Superpositionssatz-Arbeitsblatt