Python-Matrix:Beispiele für Transponierung, Multiplikation, NumPy-Arrays

Was ist Python-Matrix?

Eine Python-Matrix ist ein spezialisiertes zweidimensionales rechteckiges Array von Daten, die in Zeilen und Spalten gespeichert sind. Die Daten in einer Matrix können Zahlen, Zeichenfolgen, Ausdrücke, Symbole usw. sein. Matrix ist eine der wichtigen Datenstrukturen, die in mathematischen und wissenschaftlichen Berechnungen verwendet werden können.

In diesem Python-Tutorial lernen Sie:

Was ist Python-Matrix?
Wie funktionieren Python-Matrizen?
Python-Matrix mit einem verschachtelten Listendatentyp erstellen
Zum Lesen von Daten innerhalb der Python-Matrix mithilfe einer Liste.
Beispiel 2:Das letzte Element aus jeder Zeile lesen.
Beispiel 3:Zeilen in der Matrix drucken
Hinzufügen von Matrizen mithilfe von verschachtelten Listen
Multiplikation von Matrizen mit verschachtelten Listen
Python-Matrix mit Arrays aus dem Python-Numpy-Paket erstellen
Matrixoperation mit Numpy.Array()
Zugriff auf die NumPy-Matrix

Wie funktionieren Python-Matrizen?

Die Daten innerhalb des zweidimensionalen Arrays im Matrixformat sehen wie folgt aus:

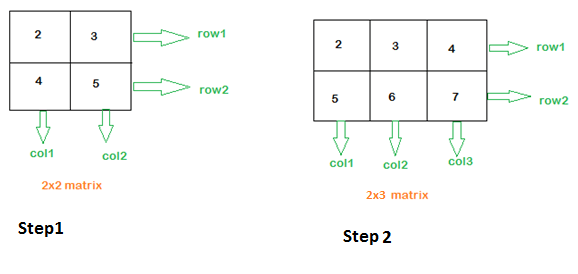
Schritt 1)

Es zeigt eine 2×2-Matrix. Es hat zwei Zeilen und 2 Spalten. Die Daten innerhalb der Matrix sind Zahlen. Die Zeile1 hat die Werte 2,3 und die Zeile2 die Werte 4,5. Die Spalten, d. h. col1, haben die Werte 2,4 und col2 hat die Werte 3,5.

Schritt 2)

Es zeigt eine 2×3-Matrix. Es hat zwei Zeilen und drei Spalten. Die Daten in der ersten Reihe, d. h. Reihe1, hat die Werte 2,3,4 und Reihe2 hat die Werte 5,6,7. Die Spalten col1 hat die Werte 2,5, col2 hat die Werte 3,6 und col3 hat die Werte 4,7.

Auf ähnliche Weise können Sie Ihre Daten in Python in der nxn-Matrix speichern. Viele Operationen können mit einer matrixähnlichen Addition, Subtraktion, Multiplikation usw. durchgeführt werden.

Python hat keine einfache Möglichkeit, einen Matrix-Datentyp zu implementieren.

Die Python-Matrix verwendet Arrays, und dasselbe kann implementiert werden.

Erstellen Sie eine Python-Matrix mit dem verschachtelten Listendatentyp
Python-Matrix mit Arrays aus dem Python-Numpy-Paket erstellen

Python-Matrix mit einem verschachtelten Listendatentyp erstellen

In Python werden die Arrays mit dem Listendatentyp dargestellt. Wir werden also jetzt die Liste verwenden, um eine Python-Matrix zu erstellen.

Wir erstellen eine 3×3-Matrix, wie unten gezeigt:

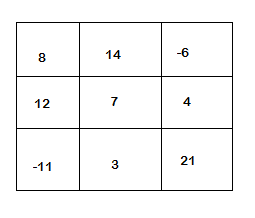
Die Matrix hat 3 Zeilen und 3 Spalten.
Die erste Zeile in einem Listenformat sieht wie folgt aus:[8,14,-6]
Die zweite Zeile in einer Liste ist:[12,7,4]
Die dritte Zeile in einer Liste ist:[-11,3,21]

Die Matrix innerhalb einer Liste mit allen Zeilen und Spalten sieht wie folgt aus:

List = [[Row1], 
           [Row2], 
           [Row3]
           ...
           [RowN]]

Gemäß der oben aufgeführten Matrix ist der Listentyp mit Matrixdaten also wie folgt:

M1 = [[8, 14, -6], [12,7,4], [-11,3,21]]

Zum Lesen von Daten innerhalb der Python-Matrix mithilfe einer Liste.

Wir verwenden die oben definierte Matrix. Das Beispiel liest die Daten, druckt die Matrix und zeigt das letzte Element aus jeder Zeile an.

Beispiel:Drucken der Matrix

M1 = [[8, 14, -6], 
           [12,7,4], 
           [-11,3,21]]

#To print the matrix
print(M1)

Ausgabe:

The Matrix M1 =  [[8, 14, -6], [12, 7, 4], [-11, 3, 21]]

Beispiel 2:Das letzte Element aus jeder Zeile lesen.

M1 = [[8, 14, -6],
           [12,7,4], 
           [-11,3,21]]

matrix_length = len(M1)

#To read the last element from each row.
for i in range(matrix_length):
    print(M1[i][-1])

Ausgabe:

-6
4
21

Beispiel 3:Zeilen in der Matrix drucken

M1 = [[8, 14, -6],
           [12,7,4], 
           [-11,3,21]]

matrix_length = len(M1)

#To print the rows in the Matrix
for i in range(matrix_length):
    print(M1[i])

Ausgabe:

[8, 14, -6]
[12, 7, 4]
[-11, 3, 21]

Hinzufügen von Matrizen mithilfe von verschachtelten Listen

Wir können zwei gegebene Matrizen leicht addieren. Die Matrizen werden hier in Listenform vorliegen. Lassen Sie uns an einem Beispiel arbeiten, das darauf achtet, die gegebenen Matrizen hinzuzufügen.

Matrix 1:

M1 = [[8, 14, -6],
           [12,7,4], 
           [-11,3,21]]

Matrix 2 :

M2 = [[3, 16, -6],
           [9,7,-4], 
           [-1,3,13]]

Last initialisiert eine Matrix, die das Ergebnis von M1 + M2 speichert.

Matrix 3 :

M3  = [[0,0,0],
            [0,0,0],
            [0,0,0]]

Beispiel:Matrizen hinzufügen

Außerdem verwenden die Matrizen eine For-Schleife, die beide angegebenen Matrizen durchläuft.

M1 = [[8, 14, -6], 
      [12,7,4], 
      [-11,3,21]]

M2 = [[3, 16, -6],
           [9,7,-4], 
           [-1,3,13]]

M3  = [[0,0,0],
       [0,0,0],
       [0,0,0]]
matrix_length = len(M1)

#To Add M1 and M2 matrices
for i in range(len(M1)):
for k in range(len(M2)):
        M3[i][k] = M1[i][k] + M2[i][k]

#To Print the matrix
print("The sum of Matrix M1 and M2 = ", M3)

Ausgabe:

The sum of Matrix M1 and M2 =  [[11, 30, -12], [21, 14, 0], [-12, 6, 34]]

Multiplikation von Matrizen mit verschachtelten Listen

Um die Matrizen zu multiplizieren, können wir die for-Schleife für beide Matrizen verwenden, wie im folgenden Code gezeigt:

M1 = [[8, 14, -6], 
      [12,7,4], 
      [-11,3,21]]

M2 = [[3, 16, -6],
           [9,7,-4], 
           [-1,3,13]]

M3  = [[0,0,0],
       [0,0,0],
       [0,0,0]]

matrix_length = len(M1)

#To Multiply M1 and M2 matrices
for i in range(len(M1)):
for k in range(len(M2)):
        M3[i][k] = M1[i][k] * M2[i][k]

#To Print the matrix
print("The multiplication of Matrix M1 and M2 = ", M3)

Ausgabe:

The multiplication of Matrix M1 and M2 =  [[24, 224, 36], [108, 49, -16], [11, 9, 273]]

Python-Matrix mit Arrays aus dem Python-Numpy-Paket erstellen

Die Python-Bibliothek Numpy hilft beim Umgang mit Arrays. Numpy verarbeitet ein Array im Vergleich zur Liste etwas schneller.

Um mit Numpy arbeiten zu können, müssen Sie es zuerst installieren. Befolgen Sie die nachstehenden Schritte, um Numpy zu installieren.

Schritt 1)

Der Befehl zum Installieren von Numpy lautet:

pip install NumPy

Schritt 2)

Um Numpy in Ihrem Code zu verwenden, müssen Sie es importieren.

import NumPy

Schritt 3)

Sie können Numpy auch mit einem Alias importieren, wie unten gezeigt:

import NumPy as np

Wir werden die Methode array() von Numpy verwenden, um eine Python-Matrix zu erstellen.

Beispiel:Array in Numpy zum Erstellen einer Python-Matrix

import numpy as np
M1 = np.array([[5, -10, 15], [3, -6, 9], [-4, 8, 12]])
print(M1)

Ausgabe:

[[  5 -10  15]
 [  3  -6   9]
 [ -4   8  12]]

Matrixoperation mit Numpy.Array()

Mögliche Matrixoperationen sind Addition, Subtraktion, Multiplikation, Transponierung, Lesen der Zeilen, Spalten einer Matrix, Aufteilen der Matrix usw. In allen Beispielen verwenden wir eine array()-Methode.

Matrixaddition

Um die Matrix zu addieren, erstellen wir zwei Matrizen mit numpy.array() und addieren sie mit dem (+)-Operator.

Beispiel:

import numpy as np

M1 = np.array([[3, 6, 9], [5, -10, 15], [-7, 14, 21]])
M2 = np.array([[9, -18, 27], [11, 22, 33], [13, -26, 39]])
M3 = M1 + M2  
print(M3)

Ausgabe:

[[ 12 -12  36]
 [ 16  12  48]
 [  6 -12  60]]

Matrixsubtraktion

Um eine Subtraktion an der Matrix durchzuführen, erstellen wir zwei Matrizen mit numpy.array() und subtrahieren sie mit dem Operator (-).

Beispiel:

import numpy as np

M1 = np.array([[3, 6, 9], [5, -10, 15], [-7, 14, 21]])
M2 = np.array([[9, -18, 27], [11, 22, 33], [13, -26, 39]])
M3 = M1 - M2  
print(M3)

Ausgabe:

[[ -6  24 -18]
 [ -6 -32 -18]
 [-20  40 -18]]

Matrixmultiplikation

Zuerst werden zwei Matrizen mit numpy.arary() erstellt. Um sie zu multiplizieren, können Sie die Methode numpy dot() verwenden. Numpy.dot() ist das Skalarprodukt der Matrix M1 und M2. Numpy.dot() verarbeitet die 2D-Arrays und führt Matrixmultiplikationen durch.

Beispiel:

import numpy as np

M1 = np.array([[3, 6], [5, -10]])
M2 = np.array([[9, -18], [11, 22]])
M3 = M1.dot(M2)  
print(M3)

Ausgabe:

[[  93   78]
 [ -65 -310]]

Matrixtransposition

Die Transponierte einer Matrix wird berechnet, indem die Zeilen als Spalten und die Spalten als Zeilen geändert werden. Die Funktion transpose() von Numpy kann verwendet werden, um die Transponierung einer Matrix zu berechnen.

Beispiel:

import numpy as np

M1 = np.array([[3, 6, 9], [5, -10, 15], [4,8,12]])
M2 = M1.transpose()

print(M2)

Ausgabe:

[[  3   5   4]
 [  6 -10   8]
 [  9  15  12]]

Slicing einer Matrix

Slicing gibt Ihnen die Elemente aus der Matrix basierend auf dem angegebenen Start-/Endindex zurück.

Die Syntax für Slicing ist – [Start:Ende]
Wenn der Startindex nicht angegeben ist, wird er als 0 betrachtet. Zum Beispiel [:5] bedeutet dies als [0:5].
Wenn das Ende nicht übergeben wird, nimmt es die Länge des Arrays an.
Wenn Start/Ende negative Werte hat, wird das Slicing vom Ende des Arrays aus erfolgen.

Bevor wir uns mit dem Slicing einer Matrix befassen, wollen wir zunächst verstehen, wie man Slice auf ein einfaches Array anwendet.

import numpy as np

arr = np.array([2,4,6,8,10,12,14,16])
print(arr[3:6]) # will print the elements from 3 to 5
print(arr[:5]) # will print the elements from 0 to 4
print(arr[2:]) # will print the elements from 2 to length of the array.
print(arr[-5:-1]) # will print from the end i.e. -5 to -2
print(arr[:-1]) # will print from end i.e. 0 to -2

Ausgabe:

[ 8 10 12]
[ 2  4  6  8 10]
[ 6  8 10 12 14 16]
[ 8 10 12 14]
[ 2  4  6  8 10 12 14]

Lassen Sie uns nun das Slicing auf matrix implementieren. Slicing auf einer Matrix durchführen

die Syntax lautet M1[row_start:row_end, col_start:col_end]

Der erste Start/das erste Ende wird für die Zeile sein, d.h. um die Zeilen der Matrix auszuwählen.
Der zweite Anfang/das zweite Ende ist für die Spalte, d. h. um die Spalten der Matrix auszuwählen.

Die Matrix M1, die wir verwenden werden, lautet wie folgt:

M1 = np.array([[2, 4, 6, 8, 10], 
    [3, 6, 9, -12, -15],
    [4, 8, 12, 16, -20],
    [5, -10, 15, -20, 25]])

Es gibt insgesamt 4 Reihen. Der Index beginnt bei 0 bis 3. Der 0^te Reihe ist die [2,4,6,8,10], 1^st Reihe ist [3,6,9,-12,-15] gefolgt von 2^nd und 3^rd .

Die Matrix M1 hat 5 Spalten. Der Index beginnt bei 0 bis 4. Der 0^te Spalte hat die Werte [2,3,4,5], 1^st Spalten haben Werte [4,6,8,-10] gefolgt von 2^nd , 3. , 4. , und 5^th .

Hier ist ein Beispiel, das zeigt, wie die Zeilen- und Spaltendaten aus der Matrix mithilfe von Slicing abgerufen werden. Im Beispiel drucken wir die 1^e und 2^nd Zeile und für Spalten wollen wir die erste, zweite und dritte Spalte. Um diese Ausgabe zu erhalten, haben wir verwendet:M1[1:3, 1:4]

Beispiel:

import numpy as np

M1 = np.array([[2, 4, 6, 8, 10], 
    [3, 6, 9, -12, -15],
    [4, 8, 12, 16, -20],
    [5, -10, 15, -20, 25]])


print(M1[1:3, 1:4]) # For 1:3, it will give first and second row.
#The columns will be taken from first to third.

Ausgabe:

[[  6   9 -12]
 [  8  12  16]]

Beispiel:Drucken aller Zeilen und dritten Spalten

import numpy as np
M1 = np.array([[2, 4, 6, 8, 10], 
    [3, 6, 9, -12, -15],
    [4, 8, 12, 16, -20],
    [5, -10, 15, -20, 25]])

print(M1[:,3]) # This will print all rows and the third column data.

Ausgabe:

[  8 -12  16 -20]

Beispiel:Drucken der ersten Zeile und aller Spalten

import numpy as np

M1 = np.array([[2, 4, 6, 8, 10], 
    [3, 6, 9, -12, -15],
    [4, 8, 12, 16, -20],
    [5, -10, 15, -20, 25]])
print(M1[:1,]) # This will print first row and all columns

Ausgabe:

[[ 2  4  6  8 10]]

Beispiel:Drucken der ersten drei Zeilen und der ersten 2 Spalten

import numpy as np

M1 = np.array([[2, 4, 6, 8, 10], 
    [3, 6, 9, -12, -15],
    [4, 8, 12, 16, -20],
    [5, -10, 15, -20, 25]])


print(M1[:3,:2])

Ausgabe:

[[2 4]
 [3 6]
 [4 8]]

Zugriff auf die NumPy-Matrix

Wir haben gesehen, wie Slicing funktioniert. Unter Berücksichtigung dessen erfahren wir, wie Sie die Zeilen und Spalten aus der Matrix erhalten.

Um die Zeilen der Matrix zu drucken

Im Beispiel werden die Zeilen der Matrix gedruckt.

Beispiel:

import numpy as np
M1 = np.array([[3, 6, 9], [5, -10, 15], [4,8,12]])
print(M1[0])  #first row
print(M1[1]) # the second row
print(M1[-1]) # -1 will print the last row

Ausgabe:

[3 6 9]
[  5 -10  15]
[ 4  8 12]

Um die letzte Zeile zu erhalten, können Sie den Index oder -1 verwenden. Beispielsweise hat die Matrix 3 Zeilen,

M1[0] gibt Ihnen also die erste Zeile,

M1[1] gibt Ihnen die zweite Reihe

M1[2] oder M1[-1] ergibt die dritte oder letzte Zeile.

Die Spalten der Matrix drucken

import numpy as np
M1 = np.array([[2, 4, 6, 8, 10], 
    [3, 6, 9, -12, -15],
    [4, 8, 12, 16, -20],
    [5, -10, 15, -20, 25]])
print(M1[:,0]) # Will print the first Column
print(M1[:,3]) # Will  print the third Column
print(M1[:,-1]) # -1 will give you the last column

Ausgabe:

[2 3 4 5]
[  8 -12  16 -20]
[ 10 -15 -20  25]

Zusammenfassung:

Eine Python-Matrix ist ein spezialisiertes zweidimensionales rechteckiges Array von Daten, die in Zeilen und Spalten gespeichert sind. Die Daten in einer Matrix können Zahlen, Zeichenfolgen, Ausdrücke, Symbole usw. sein. Matrix ist eine der wichtigen Datenstrukturen, die in mathematischen und wissenschaftlichen Berechnungen verwendet werden können.
Python bietet keine einfache Möglichkeit, einen Matrix-Datentyp zu implementieren. Eine Python-Matrix kann mit einem verschachtelten Listendatentyp und mit der numpy-Bibliothek erstellt werden.
Die Python-Bibliothek Numpy hilft beim Umgang mit Arrays. Numpy verarbeitet ein Array im Vergleich zur Liste etwas schneller.
Die möglichen Matrixoperationen sind Addition, Subtraktion, Multiplikation, Transponierung, Lesen der Zeilen, Spalten einer Matrix, Aufteilen der Matrix usw.
Um zwei Matrizen hinzuzufügen, können Sie numpy.array() verwenden und sie mit dem Operator (+) hinzufügen.
Um sie zu multiplizieren, können Sie die Methode numpy dot() verwenden. Numpy.dot() ist das Skalarprodukt der Matrix M1 und M2. Numpy.dot() verarbeitet die 2D-Arrays und führt Matrixmultiplikationen durch.
Die Transponierung einer Matrix wird berechnet, indem die Zeilen als Spalten und die Spalten als Zeilen geändert werden. Die Funktion transpose() von Numpy kann verwendet werden, um die Transponierung einer Matrix zu berechnen.
Das Aufteilen einer Matrix gibt Ihnen die Elemente basierend auf dem angegebenen Start-/Endindex zurück.

Facebook-Login mit Python:FB-Login-Beispiel Python vs. PHP:Was ist der Unterschied zwischen Python und PHP?

Python