Signiert vs. Unsigniert in VHDL
Alle Digital Designer müssen verstehen, wie Mathematik in einem FPGA oder ASIC funktioniert. Der erste Schritt dazu ist zu verstehen, wie signierte und unsignierte Signaltypen funktionieren. Vorzeichenbehaftete und unsignierte Typen existieren in numeric_std Paket, das Teil der ieee-Bibliothek ist. Es sollte beachtet werden, dass es eine weitere Paketdatei gibt, die häufig verwendet wird, um mathematische Operationen durchzuführen:std_logic_arith . std_logic_arith ist jedoch keine offizielle, von IEEE unterstützte Paketdatei und wird nicht für die Verwendung in digitalen Designs empfohlen.
Ein Signal, das als Typ signiert definiert ist bedeutet, dass die Tools dieses Signal entweder als positiv oder negativ interpretieren. Ein Signal, das als Typ unsigned definiert ist bedeutet, dass das Signal nur positiv ist. Intern verwendet das FPGA das Zweierkomplement Darstellung. Beispielsweise kann ein 3-Bit-Signal gemäß der folgenden Tabelle interpretiert werden:
Bist du schon verwirrt? Sie sollten sein, das ist nicht intuitiv! Schauen wir uns ein Beispiel an, das hoffentlich Klarheit bringt. Die folgende Datei testet, wie signiert unsigniert funktioniert. Was verstanden werden muss, ist, dass ob die Signale als signiert oder nicht signiert definiert sind oder nicht nicht gilt beeinflussen, wie die eigentliche binäre Mathematik durchgeführt wird.
Zum Beispiel:Für zwei vorzeichenbehaftete Vektoren 10001 + 00010 ist die Antwort immer noch 10011, ABER es ist die Interpretation des Ergebnisses, das anders ist.
Für den Fall ohne Vorzeichen entspricht die Antwort (10011) 19.
Für den vorzeichenbehafteten Fall repräsentiert die Antwort (10011) -13.
library ieee;
use ieee.std_logic_1164.all;
use ieee.numeric_std.all;
entity signed_unsigned is
port (
i_rst_l : in std_logic;
i_clk : in std_logic;
i_a : in std_logic_vector(4 downto 0);
i_b : in std_logic_vector(4 downto 0)
);
end signed_unsigned;
architecture behave of signed_unsigned is
signal rs_SUM_RESULT : signed(4 downto 0) := (others => '0');
signal ru_SUM_RESULT : unsigned(4 downto 0) := (others => '0');
signal rs_SUB_RESULT : signed(4 downto 0) := (others => '0');
signal ru_SUB_RESULT : unsigned(4 downto 0) := (others => '0');
begin
-- Purpose: Add two numbers. Does both the signed and unsigned
-- addition for demonstration. This process is synthesizable.
p_SUM : process (i_clk, i_rst_l)
begin
if i_rst_l = '0' then -- asynchronous reset (active low)
rs_SUM_RESULT <= (others => '0');
ru_SUM_RESULT <= (others => '0');
elsif rising_edge(i_clk) then
ru_SUM_RESULT <= unsigned(i_a) + unsigned(i_b);
rs_SUM_RESULT <= signed(i_a) + signed(i_b);
end if;
end process p_SUM;
-- Purpose: Subtract two numbers. Does both the signed and unsigned
-- subtraction for demonstration. This process is synthesizable.
p_SUB : process (i_clk, i_rst_l)
begin
if i_rst_l = '0' then -- asynchronous reset (active low)
rs_SUB_RESULT <= (others => '0');
ru_SUB_RESULT <= (others => '0');
elsif rising_edge(i_clk) then
ru_SUB_RESULT <= unsigned(i_a) - unsigned(i_b);
rs_SUB_RESULT <= signed(i_a) - signed(i_b);
end if;
end process p_SUB;
end behave;
Testbench:
library ieee;
use ieee.std_logic_1164.all;
entity example_signed_unsigned_tb is
end example_signed_unsigned_tb;
architecture behave of example_signed_unsigned_tb is
--Registers
signal r_CLK : std_logic := '0';
signal r_RST_L : std_logic := '0';
signal r_A : natural := 0;
signal r_B : natural := 0;
signal r_A_SLV : std_logic_vector(4 downto 0) := (others => '0');
signal r_B_SLV : std_logic_vector(4 downto 0) := (others => '0');
constant c_CLK_PERIOD : time := 10 ns;
component example_signed_unsigned is
port (
i_rst_l : in std_logic;
i_clk : in std_logic;
i_a : in std_logic_vector(4 downto 0);
i_b : in std_logic_vector(4 downto 0)
);
end component example_signed_unsigned;
begin
i_DUT: example_signed_unsigned
port map (
i_rst_l => r_RST_L,
i_clk => r_CLK,
i_a => r_A_SLV,
i_b => r_B_SLV
);
clk_gen : process is
begin
r_CLK <= '0' after c_CLK_PERIOD/2, '1' after c_CLK_PERIOD;
wait for c_CLK_PERIOD;
end process clk_gen;
process
begin
r_RST_L <= '0';
wait for 20 ns;
r_RST_L <= '1';
wait for 20 ns;
r_A_SLV <= "01001";
r_B_SLV <= "00110";
wait for 20 ns;
r_A_SLV <= "10001";
r_B_SLV <= "00110";
wait for 20 ns;
r_A_SLV <= "10001";
r_B_SLV <= "00001";
wait for 20 ns;
r_A_SLV <= "10001";
r_B_SLV <= "00010";
wait for 20 ns;
r_A_SLV <= "11111";
r_B_SLV <= "00001";
wait for 20 ns;
r_A_SLV <= "00000";
r_B_SLV <= "00001";
wait for 20 ns;
wait;
end process;
end behave;
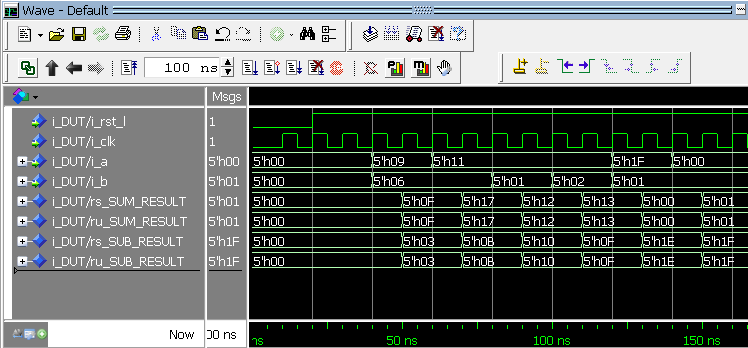Wellenausgabewerte der Modelsim-Simulation in HEX angezeigt
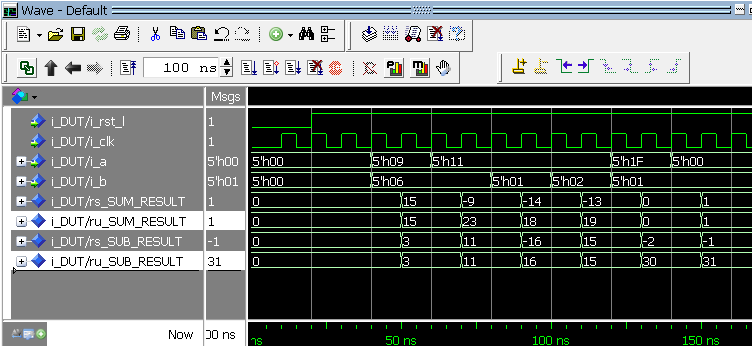Wellenausgabewerte der Modelsim-Simulation in DEZIMAL angezeigt Vergleichen Sie die beiden Modelsim-Screenshots oben. Im ersten sehen Sie die Ergebnisse der mathematischen Funktionen sind genau gleich, wenn sie in Hex dargestellt werden. Es ist die Interpretation von den Ergebnissen, die anders sind. Dies ist im unteren Screenshot zu sehen. Wenn Modelsim die Ergebnisse dezimal anzeigt, interpretiert es einige davon als negative Zahlen. Bei der Verwendung von signierten und unsignierten Typen müssen Sie sehr vorsichtig sein! Hoffentlich verstehen Sie dieses Thema etwas besser. Ich habe das Gefühl, dass dies ein Bereich ist, mit dem viele Digitaldesigner zu kämpfen haben. Wenn Sie also etwas nicht vollständig verstehen, senden Sie mir bitte eine E-Mail über den Kontaktlink in der Seitenleiste, und ich werde versuchen, es klarer zu machen.
VHDL