Neurale Netzwerkarchitektur für eine Python-Implementierung

Dieser Artikel beschreibt die Perceptron-Konfiguration, die wir für unsere Experimente mit neuronalem Netzwerktraining und -klassifizierung verwenden werden, und wir werden uns auch mit dem verwandten Thema befassen von Bias-Knoten.

Willkommen bei der Reihe von technischen Artikeln zu neuronalen Netzwerken von All About Circuits. In der bisherigen Serie – unten verlinkt – haben wir einiges an Theorie rund um neuronale Netze behandelt.

1. Wie man eine Klassifikation mit einem neuronalen Netzwerk durchführt:Was ist das Perzeptron?
2. So verwenden Sie ein einfaches Beispiel für ein neuronales Perceptron-Netzwerk zum Klassifizieren von Daten
3. Wie man ein grundlegendes neuronales Perceptron-Netzwerk trainiert
4. Einfaches neuronales Netzwerk-Training verstehen
5. Eine Einführung in die Trainingstheorie für neuronale Netze
6. Lernrate in neuronalen Netzen verstehen
7. Fortgeschrittenes maschinelles Lernen mit dem mehrschichtigen Perzeptron
8. Die Sigmoid-Aktivierungsfunktion:Aktivierung in mehrschichtigen neuronalen Perzeptronnetzen
9. Wie man ein mehrschichtiges neuronales Perceptron-Netzwerk trainiert
10. Verstehen von Trainingsformeln und Backpropagation für mehrschichtige Perzeptronen
11. Neurale Netzwerkarchitektur für eine Python-Implementierung
12. So erstellen Sie ein mehrschichtiges neuronales Perceptron-Netzwerk in Python
13. Signalverarbeitung mit neuronalen Netzen:Validierung im neuronalen Netzdesign
14. Trainings-Datasets für neuronale Netze:So trainieren und validieren Sie ein neuronales Python-Netz

Jetzt sind wir bereit, dieses theoretische Wissen in ein funktionsfähiges Perceptron-Klassifikationssystem umzuwandeln.

Zuerst möchte ich die allgemeinen Eigenschaften des Netzwerks vorstellen, die wir in einer höheren Programmiersprache implementieren werden; Ich verwende Python, aber der Code wird so geschrieben, dass er die Übersetzung in andere Sprachen wie C erleichtert. Der nächste Artikel bietet eine detaillierte Einführung in den Python-Code, und danach werden wir verschiedene Trainingsmethoden untersuchen , dieses Netzwerk nutzen und bewerten.

Die Python-Architektur des neuronalen Netzwerks

Die Software entspricht dem im folgenden Diagramm abgebildeten Perceptron.

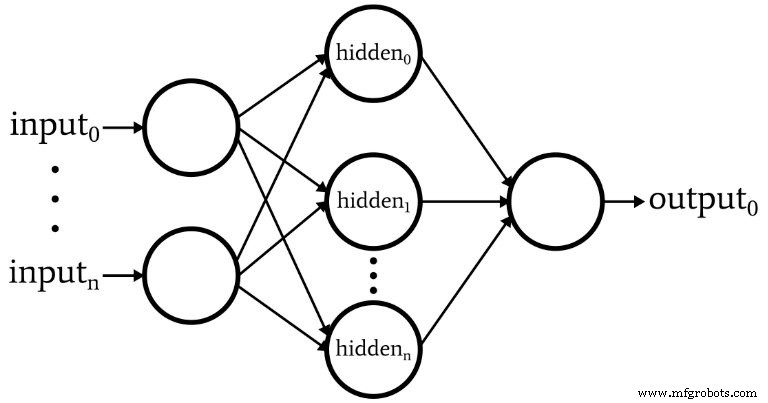
Hier sind die grundlegenden Eigenschaften des Netzwerks:

• Die Anzahl der Eingabeknoten ist variabel. Dies ist wichtig, wenn wir ein Netzwerk mit einem signifikanten Maß an Flexibilität wünschen, da die Dimensionalität der Eingabe mit der Dimensionalität der Proben übereinstimmen muss, die wir klassifizieren möchten.
• Der Code unterstützt nicht mehrere versteckte Ebenen. An dieser Stelle besteht keine Notwendigkeit – eine versteckte Schicht reicht für eine äußerst leistungsstarke Klassifizierung.
• Die Anzahl der Knoten innerhalb der einen verborgenen Schicht ist variabel. Das Finden der optimalen Anzahl versteckter Knoten erfordert einige Versuche und Irrtümer, obwohl es Richtlinien gibt, die uns helfen können, einen vernünftigen Ausgangspunkt zu wählen. Wir werden das Problem der Dimensionalität versteckter Schichten in einem zukünftigen Artikel untersuchen.
• Die Anzahl der Ausgabeknoten ist derzeit auf eins festgelegt. Diese Einschränkung macht unser anfängliches Programm etwas einfacher und wir können variable Ausgabedimensionen in eine verbesserte Version integrieren.
• Die Aktivierungsfunktion sowohl für versteckte als auch für Ausgabeknoten ist die standardmäßige logistische Sigmoid-Beziehung:

\[f(x)=\frac{1}{1+e^{-x}}\]

Was ist ein Bias-Knoten? (AKA Bias ist gut, wenn Sie ein Perceptron sind)

Während wir über die Netzwerkarchitektur sprechen, sollte ich darauf hinweisen, dass neuronale Netzwerke oft einen sogenannten Bias-Knoten enthalten (oder Sie können ihn einfach als „Bias“ ohne „Knoten“ bezeichnen). Der einem Bias-Knoten zugeordnete numerische Wert ist eine vom Designer gewählte Konstante. Zum Beispiel:

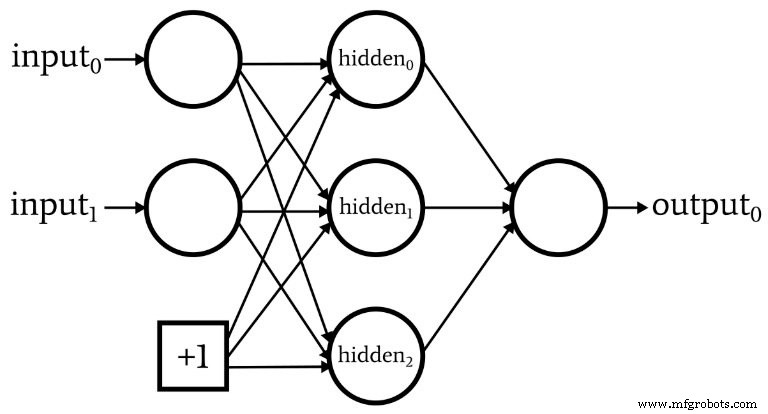
Bias-Knoten können in die Eingabeschicht oder die verborgene Schicht oder in beide integriert werden. Ihre Gewichtungen sind wie alle anderen Gewichtungen und werden mit dem gleichen Backpropagation-Verfahren aktualisiert.

Die Verwendung von Bias-Knoten ist ein wichtiger Grund, um Code für neuronale Netze zu schreiben, mit dem Sie die Anzahl der Eingabeknoten oder versteckten Knoten leicht ändern können – selbst wenn Sie nur an einer bestimmten Klassifizierungsaufgabe interessiert sind, variable Eingabe- und versteckte Dimensionalität stellt sicher, dass Sie bequem mit der Verwendung von Bias-Knoten experimentieren können.

In Teil 10 habe ich darauf hingewiesen, dass das Voraktivierungssignal eines Knotens berechnet wird, indem ein Punktprodukt ausgeführt wird, d. h. Sie multiplizieren die entsprechenden Elemente zweier Arrays (oder Vektoren, wenn Sie es vorziehen) und addieren dann alle einzelnen Produkte. Das erste Array enthält die Nachaktivierungswerte aus der vorhergehenden Schicht, und das zweite Array enthält die Gewichtungen, die die vorherige Schicht mit der aktuellen Schicht verbinden. Wenn das Postaktivierungs-Array der vorhergehenden Schicht mit x bezeichnet wird und der Gewichtungsvektor mit w bezeichnet wird, wird ein Voraktivierungswert wie folgt berechnet:

\[S_{preA} =w \cdot x =sum(w_1x_1 + w_2x_2 + \cdots + w_nx_n)\]

Sie fragen sich vielleicht, was das mit Bias-Knoten zu tun hat. Nun, der Bias (bezeichnet mit b) modifiziert dieses Verfahren wie folgt:

\[S_{preA} =( w \cdot x)+b =sum(w_1x_1 + w_2x_2 + \cdots + w_nx_n)+b\]

Ein Bias verschiebt das Signal, das von der Aktivierungsfunktion verarbeitet wird, und kann dadurch das Netzwerk flexibler und robuster machen. Die Verwendung des Buchstabens b zur Bezeichnung des Bias-Wertes erinnert an den „y-Achsenabschnitt“ in der Standardgleichung für eine Gerade:y =mx + b . Und das ist kein Zufall. Der Bias ist tatsächlich wie ein y-Achsenabschnitt, und Sie haben vielleicht auch bemerkt, dass das Array der Gewichte einer Steigung entspricht:

\[S_{preA} =( w \cdot x)+b\]

\[y =mx + b\]

Gewichte, Verzerrung und Aktivierung

Wenn wir an die numerischen Werte denken, die während des Trainings an die Aktivierungsfunktion eines Knotens geliefert werden, erhöhen oder verringern die Gewichtungen die Steigung der Eingabedaten, und der Bias verschiebt die Eingabedaten vertikal. Aber wie wirkt sich dies auf die Ausgabe des Knotens aus? Nehmen wir an, wir verwenden die Standard-Logistikfunktion zur Aktivierung:

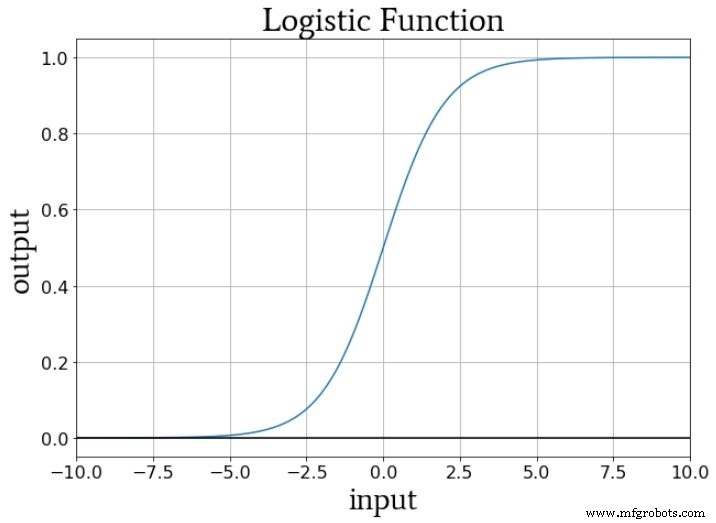
Der Übergang von f_A (x) =0 bis f_A (x) =1 wird auf einen Eingangswert von x =0 zentriert. Somit können wir durch die Verwendung eines Bias zum Erhöhen oder Verringern des Voraktivierungssignals das Auftreten des Übergangs beeinflussen und dadurch die Aktivierungsfunktion nach links oder rechts verschieben . Die Gewichte hingegen bestimmen, wie „schnell“ der Eingangswert x =0 durchläuft, was die Steilheit des Übergangs in der Aktivierungsfunktion beeinflusst.

Schlussfolgerung

Wir haben Bias-Knoten und die herausragenden Eigenschaften des ersten neuronalen Netzes besprochen, das wir in Software implementieren werden. Jetzt können wir uns den eigentlichen Code ansehen und genau das werden wir im nächsten Artikel tun.