Trainingsformeln und Backpropagation für mehrschichtige Perzeptronen verstehen

In diesem Artikel werden die Gleichungen vorgestellt, die wir bei der Berechnung der Gewichtungsaktualisierung verwenden, und wir diskutieren auch das Konzept der Backpropagation.

Willkommen zur AAC-Serie zum maschinellen Lernen.

Informieren Sie sich hier über die bisherige Serie:

1. Wie man eine Klassifikation mit einem neuronalen Netzwerk durchführt:Was ist das Perzeptron?
2. So verwenden Sie ein einfaches Beispiel für ein neuronales Perceptron-Netzwerk zum Klassifizieren von Daten
3. Wie man ein grundlegendes neuronales Perceptron-Netzwerk trainiert
4. Einfaches neuronales Netzwerk-Training verstehen
5. Eine Einführung in die Trainingstheorie für neuronale Netze
6. Lernrate in neuronalen Netzen verstehen
7. Fortgeschrittenes maschinelles Lernen mit dem mehrschichtigen Perzeptron
8. Die Sigmoid-Aktivierungsfunktion:Aktivierung in mehrschichtigen neuronalen Perzeptronnetzen
9. Wie man ein mehrschichtiges neuronales Perceptron-Netzwerk trainiert
10. Verstehen von Trainingsformeln und Backpropagation für mehrschichtige Perzeptronen
11. Neurale Netzwerkarchitektur für eine Python-Implementierung
12. So erstellen Sie ein mehrschichtiges neuronales Perceptron-Netzwerk in Python
13. Signalverarbeitung mit neuronalen Netzen:Validierung im neuronalen Netzdesign
14. Trainings-Datasets für neuronale Netze:So trainieren und validieren Sie ein neuronales Python-Netz

Wir sind an dem Punkt angelangt, an dem wir ein grundlegendes Thema der neuronalen Netztheorie sorgfältig prüfen müssen:das Rechenverfahren, das es uns ermöglicht, die Gewichte eines mehrschichtigen Perceptrons (MLP) so fein abzustimmen, dass es Eingabeabtastwerte genau klassifizieren kann. Dies führt uns zum Konzept der „Backpropagation“, das ein wesentlicher Aspekt des Designs neuronaler Netze ist.

Gewichtungen aktualisieren

Die Informationen rund um die Ausbildung für MLPs sind kompliziert. Erschwerend kommt hinzu, dass Online-Ressourcen unterschiedliche Terminologien und Symbole verwenden, und sie scheinen sogar zu unterschiedlichen Ergebnissen zu kommen. Ich bin mir jedoch nicht sicher, ob die Ergebnisse wirklich unterschiedlich sind oder nur die gleichen Informationen auf unterschiedliche Weise präsentiert werden.

Die in diesem Artikel enthaltenen Gleichungen basieren auf den Herleitungen und Erläuterungen von Dr. Dustin Stansbury in diesem Blogbeitrag. Seine Behandlung ist die beste, die ich gefunden habe, und es ist ein großartiger Ausgangspunkt, wenn Sie sich mit den mathematischen und konzeptionellen Details des Gradientenabstiegs und der Backpropagation befassen möchten.

Das folgende Diagramm stellt die Architektur dar, die wir in Software implementieren werden, und die folgenden Gleichungen entsprechen dieser Architektur, die im nächsten Artikel ausführlicher erörtert wird.

Terminologie

Dieses Thema wird schnell unüberschaubar, wenn wir keine klare Terminologie pflegen. Ich verwende die folgenden Begriffe:

• Voraktivierung (abgekürzt \(S_{preA}\) ):Dies bezieht sich auf das Signal (eigentlich nur eine Zahl im Kontext einer Trainingsiteration), das als Eingabe für die Aktivierungsfunktion eines Knotens dient. Es wird berechnet, indem ein Punktprodukt ausgeführt wird eines Arrays, das Gewichte enthält, und eines Arrays, das die Werte enthält, die von Knoten in der vorherigen Schicht stammen. Das Punktprodukt entspricht einer elementweisen Multiplikation der beiden Arrays und der anschließenden Summation der Elemente in dem aus dieser Multiplikation resultierenden Array.
• Postaktivierung (abgekürzt \(S_{postA}\) ):Dies bezieht sich auf das Signal (wieder nur eine Zahl im Kontext einer einzelnen Iteration), das einen Knoten verlässt. Es wird erzeugt, indem die Aktivierungsfunktion auf das Voraktivierungssignal angewendet wird. Mein bevorzugter Begriff für die Aktivierungsfunktion, bezeichnet mit \(f_{A}()\) , ist logistisch anstatt sigmoid.
• Im Python-Code sehen Sie Gewichtsmatrizen, die mit ItoH labeled gekennzeichnet sind und HtoO . Ich verwende diese Bezeichner, weil es mehrdeutig ist, so etwas wie „Hidden-Layer-Gewichtungen“ zu sagen – wären dies die Gewichtungen, die vor angewendet wurden? die versteckte Ebene oder nach die versteckte Schicht? In meinem Schema gibt ItoH die Gewichtungen an, die auf Werte angewendet werden, die von den Eingabeknoten an die versteckten Knoten übertragen werden, und HtoO gibt die Gewichtungen an, die auf Werte angewendet werden, die von den versteckten Knoten an den Ausgabeknoten übertragen werden.
• Der korrekte Ausgabewert für eine Trainingsprobe wird als Ziel bezeichnet und wird mit T . bezeichnet .
• Lernrate wird abgekürzt als LR .
• Endgültiger Fehler ist die Differenz zwischen dem Postaktivierungssignal vom Ausgangsknoten (\(S_{postA,O}\) ) und das Ziel, berechnet als \(FE =S_{postA,O} - T\) .
• Fehlersignal (\(S_{ERROR}\) ) ist der letzte Fehler, der durch die Aktivierungsfunktion des Ausgabeknotens zurück zur versteckten Schicht weitergegeben wird.
• Farbverlauf repräsentiert den Beitrag einer gegebenen Gewichtung zum Fehlersignal. Wir modifizieren die Gewichte, indem wir diesen Beitrag (ggf. multipliziert mit der Lernrate) subtrahieren.

Das folgende Diagramm verortet einige dieser Begriffe innerhalb der visualisierten Konfiguration des Netzwerks. Ich weiß – es sieht aus wie ein buntes Durcheinander. Ich entschuldige mich. Es ist ein Diagramm mit hoher Informationsdichte, und obwohl es auf den ersten Blick etwas anstößig sein mag, denke ich, dass Sie es sehr hilfreich finden werden, wenn Sie es sorgfältig studieren.

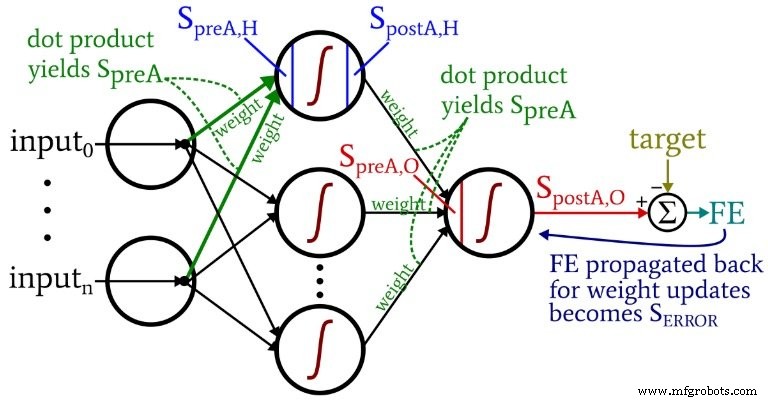
Die Gewichtungs-Update-Gleichungen werden abgeleitet, indem die partielle Ableitung der Fehlerfunktion (wir verwenden den summierten quadratischen Fehler, siehe Teil 8 der Serie, der sich mit den Aktivierungsfunktionen befasst) in Bezug auf das zu modifizierende Gewicht gebildet wird. Bitte lesen Sie den Beitrag von Dr. Stansbury, wenn Sie die Mathematik sehen möchten; In diesem Artikel springen wir direkt zu den Ergebnissen. Für die Hidden-to-Output-Gewichtungen haben wir Folgendes:

\[S_{ERROR} =FE \times {f_A}'(S_{preA,O})\]

\[gradient_{HtoO}=S_{ERROR}\times S_{postA,H}\]

\[weight_{HtoO} =weight_{HtoO}- (LR \times gradient_{HtoO})\]

Wir berechnen das Fehlersignal l durch Multiplikation des endgültigen Fehlers durch den Wert, der erzeugt wird, wenn wir das Derivat . anwenden der Aktivierungsfunktion zum Voraktivierungssignal an den Ausgangsknoten geliefert (beachten Sie das Primsymbol, das die erste Ableitung in \({f_A}'(S_{preA,O})\) anzeigt). Der Gradient wird dann durch Multiplikation des Fehlersignals . berechnet durch das Postaktivierungssignal aus der versteckten Schicht. Schließlich aktualisieren wir das Gewicht, indem wir diesen Gradienten abziehen aus dem aktuellen Gewichtswert, und wir können den Gradienten multiplizieren nach der Lernrate wenn wir die Schrittweite ändern möchten.

Für die Gewichtungen von der Eingabe bis zum Verborgenen haben wir Folgendes:

\[gradient_{ItoH} =FE \times {f_A}'(S_{preA,O})\times weight_{HtoO} \times {f_A}'(S_{preA ,H}) \times Eingabe\]

\[\Rightarrow gradient_{ItoH} =S_{ERROR} \times weight_{HtoO} \times {f_A}'(S_{preA,H})\times input\]

\[weight_{ItoH} =weight_{ItoH} - (LR \times gradient_{ItoH})\]

Bei den Eingabe-zu-Versteckten-Gewichtungen muss der Fehler durch eine zusätzliche Schicht zurück propagiert werden, und wir tun dies, indem wir dasFehlersignal . multiplizieren durch das Hidden-to-Output-Gewicht mit dem versteckten interessierenden Knoten verbunden. Wenn wir also eine Eingabe-zu-ausgeblendete Gewichtung aktualisieren das zum ersten versteckten Knoten führt, multiplizieren wir das Fehlersignal durch die Gewichtung, die den ersten versteckten Knoten mit dem Ausgabeknoten verbindet. Wir vervollständigen dann die Berechnung, indem wir Multiplikationen analog zu denen der Aktualisierungen des versteckten Ausgangsgewichts durchführen:Wir wenden die Ableitung . an der Aktivierungsfunktion zum Voraktivierungssignal des versteckten Knotens , und der "Input"-Wert kann als das Nachaktivierungssignal betrachtet werden vom Eingabeknoten.

Backpropagation

Die obige Erläuterung hat bereits das Konzept der Backpropagation berührt. Ich möchte dieses Konzept nur kurz bekräftigen und sicherstellen, dass Sie mit diesem Begriff, der in Diskussionen über neuronale Netze häufig vorkommt, explizit vertraut sind.

Backpropagation ermöglicht es uns, das in Teil 8 diskutierte Dilemma mit versteckten Knoten zu überwinden. Wir müssen die Gewichte von Input zu Hidden basierend auf der Differenz zwischen der generierten Ausgabe des Netzwerks und den Zielausgabewerten der Trainingsdaten aktualisieren, aber diese Gewichte beeinflussen die erzeugte Ausgabe indirekt.

Backpropagation bezieht sich auf die Technik, bei der wir ein Fehlersignal zurück zu einer oder mehreren versteckten Schichten senden und dieses Fehlersignal skalieren, indem wir sowohl die Gewichte verwenden, die von einem versteckten Knoten ausgehen, als auch die Ableitung der Aktivierungsfunktion des versteckten Knotens. Das Gesamtverfahren dient als Möglichkeit, eine Gewichtung basierend auf dem Beitrag der Gewichtung zum Ausgabefehler zu aktualisieren, auch wenn dieser Beitrag durch die indirekte Beziehung zwischen einer Eingabe-zu-ausgeblendeten Gewichtung und dem generierten Ausgabewert verdeckt wird.

Schlussfolgerung

Wir haben viele wichtige Materialien behandelt. Ich denke, dass wir in diesem Artikel einige wirklich wertvolle Informationen über das Training neuronaler Netze haben, und ich hoffe, dass Sie mir zustimmen. Die Serie wird noch spannender, also schau noch mal nach neuen Teilen.