So erstellen Sie ein mehrschichtiges neuronales Perceptron-Netzwerk in Python

Dieser Artikel führt Sie Schritt für Schritt durch ein Python-Programm, mit dem wir ein neuronales Netzwerk trainieren und eine erweiterte Klassifizierung durchführen können.

Dies ist der 12. Eintrag in der Serie zur Entwicklung neuronaler Netze von AAC. Sehen Sie unten, was die Serie sonst noch bietet:

1. Wie man eine Klassifikation mit einem neuronalen Netzwerk durchführt:Was ist das Perzeptron?
2. So verwenden Sie ein einfaches Beispiel für ein neuronales Perceptron-Netzwerk zum Klassifizieren von Daten
3. Wie man ein grundlegendes neuronales Perceptron-Netzwerk trainiert
4. Einfaches neuronales Netzwerk-Training verstehen
5. Eine Einführung in die Trainingstheorie für neuronale Netze
6. Lernrate in neuronalen Netzen verstehen
7. Fortgeschrittenes maschinelles Lernen mit dem mehrschichtigen Perzeptron
8. Die Sigmoid-Aktivierungsfunktion:Aktivierung in mehrschichtigen neuronalen Perzeptronnetzwerken
9. Wie man ein mehrschichtiges neuronales Perceptron-Netzwerk trainiert
10. Verstehen von Trainingsformeln und Backpropagation für mehrschichtige Perzeptronen
11. Neurale Netzwerkarchitektur für eine Python-Implementierung
12. So erstellen Sie ein mehrschichtiges neuronales Perceptron-Netzwerk in Python
13. Signalverarbeitung mit neuronalen Netzen:Validierung im neuronalen Netzdesign
14. Trainings-Datasets für neuronale Netze:So trainieren und validieren Sie ein neuronales Python-Netz

In diesem Artikel nehmen wir die Arbeit, die wir an neuronalen Perceptron-Netzwerken gemacht haben, und lernen, wie man eines in einer vertrauten Sprache implementiert:Python.

Verständlichen Python-Code für neuronale Netze entwickeln

In letzter Zeit habe ich mir einige Online-Ressourcen für neuronale Netze angesehen, und obwohl es zweifellos viele gute Informationen gibt, war ich mit den Software-Implementierungen, die ich gefunden habe, nicht zufrieden. Sie waren immer zu komplex, zu dicht oder nicht intuitiv genug. Als ich mein neuronales Python-Netzwerk schrieb, wollte ich wirklich etwas entwickeln, das den Leuten helfen kann, zu lernen, wie das System funktioniert und wie die Theorie des neuronalen Netzwerks in Programmanweisungen übersetzt wird.

Es besteht jedoch manchmal eine umgekehrte Beziehung zwischen der Klarheit des Codes und der Effizienz des Codes. Das Programm, das wir in diesem Artikel besprechen werden, ist definitiv nicht optimiert für schnelle Leistung. Optimierung ist ein ernstes Thema im Bereich neuronaler Netze; reale Anwendungen können einen immensen Schulungsaufwand erfordern, und folglich kann eine gründliche Optimierung zu einer erheblichen Reduzierung der Verarbeitungszeit führen. Für einfache Experimente wie die, die wir durchführen werden, dauert das Training jedoch nicht sehr lange, und es gibt keinen Grund, Codierungspraktiken zu betonen, die Einfachheit und Verständnis der Geschwindigkeit vorziehen.

Das gesamte Python-Programm ist als Bild am Ende dieses Artikels enthalten und die Datei („MLP_v1.py“) wird als Download bereitgestellt. Der Code führt sowohl Training als auch Validierung durch; Dieser Artikel konzentriert sich auf das Training, und wir werden später auf die Validierung eingehen. In jedem Fall gibt es jedoch nicht viele Funktionen im Validierungsteil, die nicht im Trainingsteil behandelt werden.

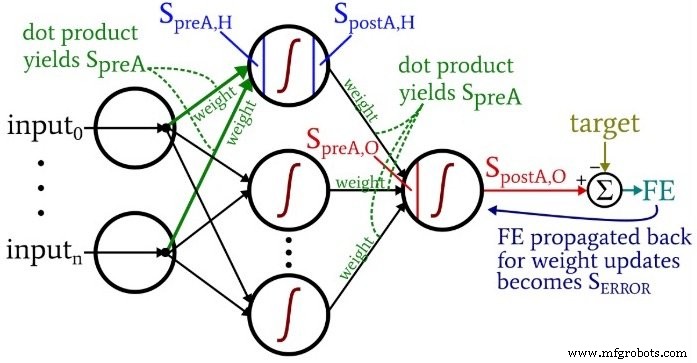
Wenn Sie über den Code nachdenken, möchten Sie vielleicht auf das etwas überwältigende, aber sehr informative Architektur-plus-Terminologie-Diagramm zurückblicken, das ich in Teil 10 bereitgestellt habe.

Vorbereiten von Funktionen und Variablen

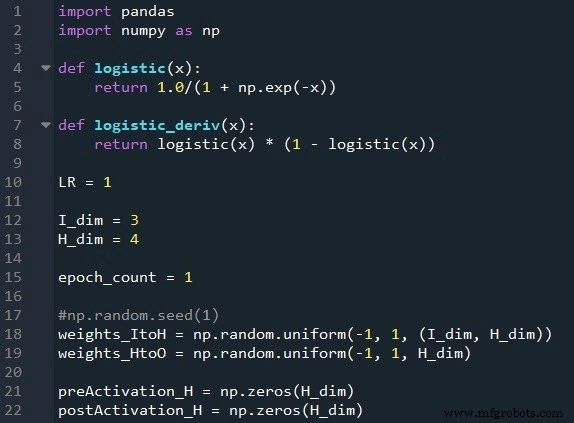
Die NumPy-Bibliothek wird häufig für die Berechnungen des Netzwerks verwendet, und die Pandas-Bibliothek bietet mir eine bequeme Möglichkeit, Trainingsdaten aus einer Excel-Datei zu importieren.

Wie Sie bereits wissen, verwenden wir zur Aktivierung die logistische Sigmoid-Funktion. Wir benötigen die logistische Funktion selbst zur Berechnung der Postaktivierungswerte, und die Ableitung der logistischen Funktion wird für die Backpropagation benötigt.

Als nächstes wählen wir die Lernrate, die Dimensionalität der Eingabeschicht, die Dimensionalität der versteckten Schicht und die Epochenzahl. Das Training über mehrere Epochen hinweg ist für echte neuronale Netze wichtig, da Sie so mehr aus Ihren Trainingsdaten lernen können. Wenn Sie Trainingsdaten in Excel generieren, müssen Sie nicht mehrere Epochen ausführen, da Sie problemlos weitere Trainingsbeispiele erstellen können.

Die np.random.uniform() Funktion füllt unsere beiden Gewichtungsmatrizen mit Zufallswerten zwischen –1 und +1. (Beachten Sie, dass die versteckte Ausgabematrix eigentlich nur ein Array ist, da wir nur einen Ausgabeknoten haben.) Die np.random.seed(1) -Anweisung bewirkt, dass die Zufallswerte bei jeder Ausführung des Programms gleich sind. Die anfänglichen Gewichtungswerte können einen erheblichen Einfluss auf die endgültige Leistung des trainierten Netzwerks haben. Wenn Sie also versuchen zu beurteilen, wie andere Variablen die Leistung verbessern oder verschlechtern, können Sie diese Anweisung auskommentieren und dadurch den Einfluss der Zufallsgewichtungsinitialisierung eliminieren.

Schließlich erstelle ich leere Arrays für die Voraktivierungs- und Nachaktivierungswerte in der verborgenen Ebene.

Importieren von Trainingsdaten

Dies ist das gleiche Verfahren, das ich bereits in Teil 4 verwendet habe. Ich importiere Trainingsdaten aus Excel, trenne die Zielwerte in der Spalte „Output“ aus, entferne die Spalte „Output“, wandle die Trainingsdaten in eine NumPy-Matrix um und speichere die Anzahl der Trainingsproben im training_count variabel.

Feedforward-Verarbeitung

Die Berechnungen, die einen Ausgabewert erzeugen und bei denen sich Daten in einem typischen neuronalen Netzwerkdiagramm von links nach rechts bewegen, bilden den „Feedforward“-Teil des Systembetriebs. Hier ist der Feedforward-Code:

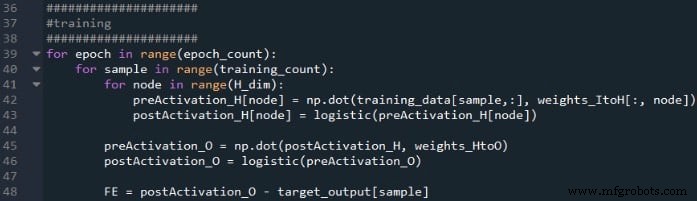
Die erste for-Schleife ermöglicht es uns, mehrere Epochen zu haben. Innerhalb jeder Epoche berechnen wir einen Ausgabewert (d. h. das Nachaktivierungssignal des Ausgabeknotens) für jede Abtastung, und diese Abtastung für Abtastung wird von der zweiten for-Schleife erfasst. In der dritten for-Schleife kümmern wir uns individuell um jeden versteckten Knoten, indem wir das Punktprodukt verwenden, um das Voraktivierungssignal zu erzeugen, und die Aktivierungsfunktion, um das Nachaktivierungssignal zu erzeugen.

Danach sind wir bereit, das Voraktivierungssignal für den Ausgangsknoten zu berechnen (wiederum unter Verwendung des Punktprodukts) und wenden die Aktivierungsfunktion an, um das Nachaktivierungssignal zu generieren. Dann subtrahieren wir das Ziel vom Postaktivierungssignal des Ausgangsknotens, um den endgültigen Fehler zu berechnen.

Backpropagation

Nachdem wir die Feedforward-Berechnungen durchgeführt haben, ist es an der Zeit, die Richtungen umzukehren. Im Backpropagation-Teil des Programms bewegen wir uns vom Ausgabeknoten zu den Hidden-to-Output-Gewichtungen und dann den Input-to-hidden-Gewichten, was die Fehlerinformationen mitbringt, die wir verwenden, um das Netzwerk effektiv zu trainieren.

Wir haben hier zwei Ebenen von for-Schleifen:eine für die Hidden-to-Output-Gewichtungen und eine für die Input-to-hidden-Gewichtungen. Wir generieren zuerst S_ERROR , die wir für die Berechnung sowohl des Gradienten_HtoO . benötigen und Steigung_ItoH , und dann aktualisieren wir die Gewichtungen, indem wir den Gradienten multipliziert mit der Lernrate subtrahieren.

Beachten Sie, wie die Gewichtungen von der Eingabe bis zum Verborgenen innerhalb aktualisiert werden die Hidden-to-Output-Schleife. Wir beginnen mit dem Fehlersignal, das zu einem der versteckten Knoten zurückführt, dann erweitern wir dieses Fehlersignal auf alle Eingangsknoten, die mit diesem einen versteckten Knoten verbunden sind:

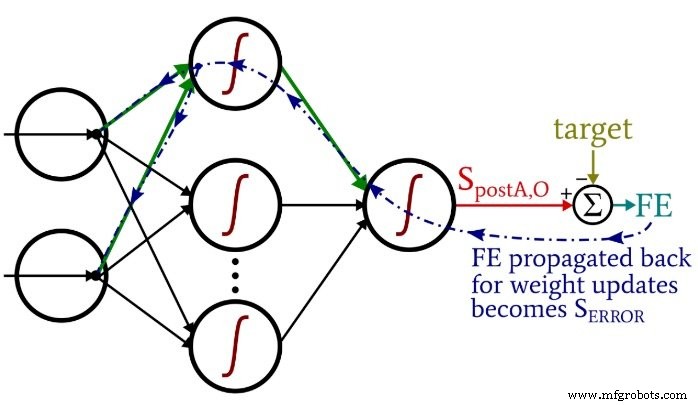
Nachdem alle Gewichtungen (sowohl ItoH als auch HtoO), die diesem einen versteckten Knoten zugeordnet sind, aktualisiert wurden, schleifen wir zurück und beginnen erneut mit dem nächsten versteckten Knoten.

Beachten Sie auch, dass die ItoH-Gewichte vor den HtoO-Gewichten geändert werden. Wir verwenden das aktuelle HtoO-Gewicht, wenn wir den Gradienten berechnen_ItoH , daher möchten wir die HtoO-Gewichte nicht ändern, bevor diese Berechnung durchgeführt wurde.

Schlussfolgerung

Es ist interessant, darüber nachzudenken, wie viel Theorie in dieses relativ kurze Python-Programm gesteckt wurde. Ich hoffe, dass dieser Code Ihnen hilft, wirklich zu verstehen, wie wir ein mehrschichtiges neuronales Perceptron-Netzwerk in Software implementieren können.

Meinen vollständigen Code finden Sie unten:

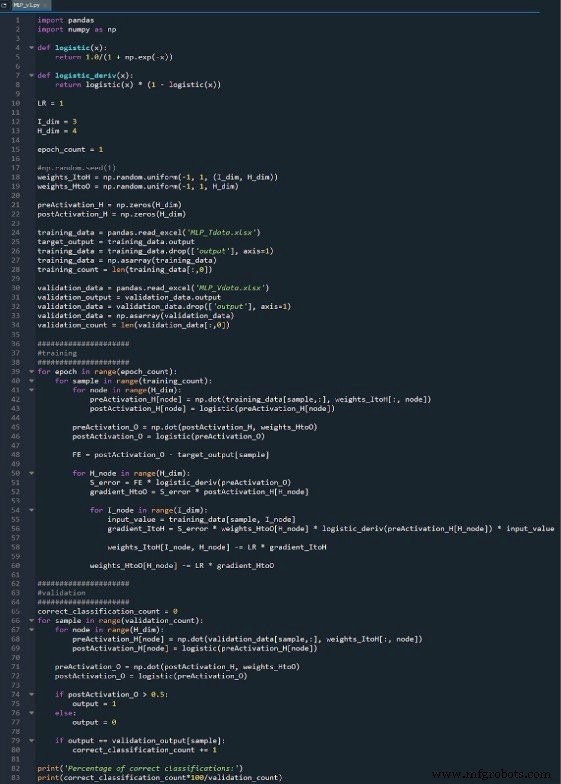
Code herunterladen