Wie man ein grundlegendes neuronales Perceptron-Netzwerk trainiert
Dieser Artikel stellt Python-Code vor, mit dem Sie automatisch Gewichte für ein einfaches neuronales Netzwerk generieren können.
Willkommen zur AAC-Serie über neuronale Perceptron-Netzwerke. Wenn Sie für Hintergrundinformationen von vorne beginnen oder nach vorne springen möchten, lesen Sie den Rest der Artikel hier:
- Wie man eine Klassifikation mit einem neuronalen Netzwerk durchführt:Was ist das Perzeptron?
- So verwenden Sie ein einfaches Beispiel für ein neuronales Perceptron-Netzwerk zum Klassifizieren von Daten
- Wie man ein grundlegendes neuronales Perceptron-Netzwerk trainiert
- Einfaches neuronales Netzwerk-Training verstehen
- Eine Einführung in die Trainingstheorie für neuronale Netze
- Lernrate in neuronalen Netzen verstehen
- Fortgeschrittenes maschinelles Lernen mit dem mehrschichtigen Perzeptron
- Die Sigmoid-Aktivierungsfunktion:Aktivierung in mehrschichtigen neuronalen Perzeptronnetzwerken
- Wie man ein mehrschichtiges neuronales Perceptron-Netzwerk trainiert
- Verstehen von Trainingsformeln und Backpropagation für mehrschichtige Perzeptronen
- Neurale Netzwerkarchitektur für eine Python-Implementierung
- So erstellen Sie ein mehrschichtiges neuronales Perceptron-Netzwerk in Python
- Signalverarbeitung mit neuronalen Netzen:Validierung im neuronalen Netzdesign
- Trainings-Datasets für neuronale Netze:So trainieren und validieren Sie ein neuronales Python-Netz
Klassifikation mit einem einschichtigen Perzeptron
Im vorherigen Artikel wurde eine einfache Klassifikationsaufgabe vorgestellt, die wir aus der Perspektive der neuronalen Netzwerk-basierten Signalverarbeitung untersucht haben. Die für diese Aufgabe erforderliche mathematische Beziehung war so einfach, dass ich das Netzwerk entwerfen konnte, indem ich nur darüber nachdachte, wie ein bestimmter Satz von Gewichtungen es dem Ausgabeknoten ermöglichen würde, die Eingabedaten korrekt zu kategorisieren.
Dies ist das Netzwerk, das ich entworfen habe:
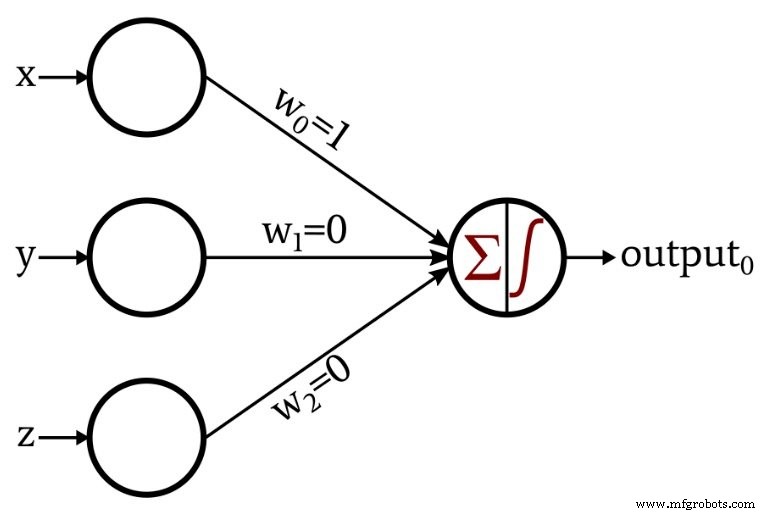
Die Aktivierungsfunktion im Ausgangsknoten ist der Einheitenschritt:
\[f(x)=\begin{cases}0 &x <0\\1 &x \geq 0\end{cases}\]
Die Diskussion wurde etwas interessanter, als ich ein Netzwerk vorstellte, das durch das als Training bekannte Verfahren seine eigenen Gewichte erzeugte:
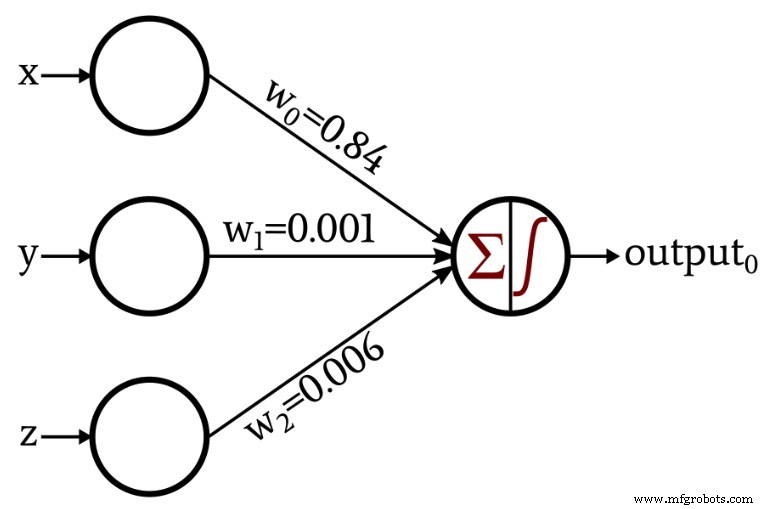
Im Rest dieses Artikels untersuchen wir den Python-Code, mit dem ich diese Gewichtungen erhalten habe.
Ein neuronales Python-Netzwerk
Hier ist der Code:
Sehen wir uns diese Anweisungen genauer an.
Netzwerk konfigurieren und Daten organisieren
input_dim =3
Die Dimensionalität ist einstellbar. Unsere Eingabedaten bestehen, wenn Sie sich erinnern, aus dreidimensionalen Koordinaten, daher benötigen wir drei Eingabeknoten. Dieses Programm unterstützt nicht mehrere Ausgabeknoten, aber wir werden die anpassbare Ausgabedimensionalität in ein zukünftiges Experiment einbeziehen.
Lernrate =0,01
Wir werden die Lernrate in einem zukünftigen Artikel besprechen.
Gewichte =np.random.rand(input_dim) #Gewichte[0] =0,5 #Gewichte[1] =0,5 #Gewichte[2] =0,5
Gewichte werden normalerweise auf Zufallswerte initialisiert. Die Funktion numpy random.rand() generiert ein Array der Länge input_dim gefüllt mit Zufallswerten verteilt über das Intervall [0, 1). Die anfänglichen Gewichtungswerte beeinflussen jedoch die durch das Trainingsverfahren erzeugten endgültigen Gewichtungswerte. Wenn Sie also die Auswirkungen anderer Variablen (wie Trainingssatzgröße oder Lernrate) bewerten möchten, können Sie diesen Störfaktor entfernen, indem Sie alle gewichtet auf eine bekannte Konstante statt auf eine zufällig generierte Zahl.
Training_Data =pandas.read_excel("3D_data.xlsx") Ich verwende die Pandas-Bibliothek, um Trainingsdaten aus einer Excel-Tabelle zu importieren. Im nächsten Artikel wird auf die Trainingsdaten näher eingegangen.
Expected_Output =Training_Data.output Training_Data =Training_Data.drop(['output'], axis=1)
Der Trainingsdatensatz enthält Eingabewerte und entsprechende Ausgabewerte. Die erste Anweisung trennt die Ausgabewerte und speichert sie in einem separaten Array, und die nächste Anweisung entfernt die Ausgabewerte aus dem Trainingsdatensatz.
Training_Data =np.asarray(Training_Data) training_count =len(Training_Data[:,0])
Ich wandele den Trainingsdatensatz, der derzeit eine Pandas-Datenstruktur ist, in ein numpy-Array um und schaue mir dann die Länge einer der Spalten an, um zu bestimmen, wie viele Datenpunkte für das Training verfügbar sind.
Berechnung von Ausgabewerten
für Epoche im Bereich(0,5):
Die Länge einer Trainingseinheit richtet sich nach der Anzahl der verfügbaren Trainingsdaten. Sie können die Gewichtungen jedoch weiter optimieren, indem Sie das Netzwerk mehrmals mit demselben Datensatz trainieren. Die Vorteile des Trainings verschwinden nicht, nur weil das Netzwerk diese Trainingsdaten bereits gesehen hat. Jeder vollständige Durchlauf durch den gesamten Trainingssatz wird als Epoche bezeichnet.
für Datum im Bereich(0, training_count):
Die in dieser Schleife enthaltene Prozedur tritt einmal für jede Zeile im Trainingssatz auf, wobei sich „row“ auf eine Gruppe von Eingabedatenwerten und den entsprechenden Ausgabewert bezieht (in unserem Fall besteht eine Eingabegruppe aus drei Zahlen, die x, y . darstellen). , und z-Komponenten eines Punktes im dreidimensionalen Raum).
Output_Sum =np.sum(np.multiply(Training_Data[datum,:], Gewichte))
Der Ausgabeknoten muss die von den drei Eingabeknoten gelieferten Werte summieren. Meine Python-Implementierung tut dies, indem sie zuerst eine elementweise Multiplikation des Training_Data-Arrays durchführt und die Gewichte Array und dann Berechnen der Summe der Elemente in dem Array, das durch diese Multiplikation erzeugt wird.
wenn Output_Sum <0:Output_Value =0 anders:Output_Value =1
Eine if-else-Anweisung wendet die Einheitsschritt-Aktivierungsfunktion an:Wenn die Summation kleiner als null ist, ist der vom Ausgangsknoten generierte Wert 0; wenn die Summe gleich oder größer Null ist, ist der Ausgabewert Eins.
Gewichtungen aktualisieren
Wenn die erste Ausgabeberechnung abgeschlossen ist, haben wir Gewichtungswerte, aber sie helfen uns nicht bei der Klassifizierung, da sie zufällig generiert werden. Wir machen das neuronale Netz zu einem effektiven Klassifikationssystem, indem wir die Gewichte wiederholt so modifizieren, dass sie allmählich die mathematische Beziehung zwischen den Eingabedaten und den gewünschten Ausgabewerten widerspiegeln. Die Gewichtsmodifikation wird durch Anwenden der folgenden Lernregel für jede Reihe im Trainingssatz erreicht:
\[w_{new} =w+(\alpha\times(output_{expected}-output_{berechnet})\times input)\]
Das Symbol \( \alpha \) bezeichnet die Lernrate. Um einen neuen Gewichtswert zu berechnen, multiplizieren wir also den entsprechenden Eingabewert mit der Lernrate und mit der Differenz zwischen der erwarteten Ausgabe (die vom Trainingssatz bereitgestellt wird) und der berechneten Ausgabe, und dann wird das Ergebnis dieser Multiplikation addiert auf den aktuellen Gewichtswert. Wenn wir Delta definieren (\(\delta\) ) als (\(Ausgabe_{erwartet} - Ausgabe_{berechnet}\)), können wir dies umschreiben als
\[w_{new} =w+(\alpha\times\delta\times Eingabe)\]
So habe ich die Lernregel in Python implementiert:
error =Expected_Output[datum] - Output_Value für n im Bereich (0, input_dim):Gewichte[n] =Gewichte[n] + learning_rate*error*Training_Data[datum,n]
Schlussfolgerung
Sie haben jetzt Code, den Sie zum Trainieren eines Perceptrons mit einer einzelnen Schicht und einem einzelnen Ausgabeknoten verwenden können. Wir werden im nächsten Artikel mehr Details über die Theorie und Praxis des neuronalen Netzwerktrainings untersuchen.
Eingebettet
- Einfaches Intrusion Detection System
- Ausbildung zum Autoelektriker
- Wie Sie Ihre Geräte härten, um Cyber-Angriffe zu verhindern
- Wie man einen Algorithmus trainiert, um frühzeitige Erblindung zu erkennen und zu verhindern
- CEVA:KI-Prozessor der zweiten Generation für tiefe neuronale Netzwerk-Workloads
- Einfaches IoT – RaspberryPI HDC2010 wie es geht
- Was ist ein Netzwerksicherheitsschlüssel? Wie finde ich es?
- 5 grundlegende Tipps zur Netzwerksicherheit für kleine Unternehmen
- Wie sicher ist Ihr Fertigungsnetzwerk?
- Wie bildet Industrie 4.0 die Arbeitskräfte von morgen aus?



