Ein einfaches Beispiel für ein neuronales Perceptron-Netzwerk zum Klassifizieren von Daten verwenden

Dieser Artikel demonstriert die grundlegende Funktionalität eines neuronalen Netzwerks von Perceptron und erklärt den Zweck des Trainings.

Dieser Artikel ist Teil einer Serie über neuronale Perceptron-Netzwerke.

Wenn Sie von vorne beginnen oder nach vorne springen möchten, können Sie sich hier die anderen Artikel ansehen:

1. Wie man eine Klassifikation mit einem neuronalen Netzwerk durchführt:Was ist das Perzeptron?
2. So verwenden Sie ein einfaches Beispiel für ein neuronales Perceptron-Netzwerk zum Klassifizieren von Daten
3. Wie man ein grundlegendes neuronales Perceptron-Netzwerk trainiert
4. Einfaches neuronales Netzwerk-Training verstehen
5. Eine Einführung in die Trainingstheorie für neuronale Netze
6. Lernrate in neuronalen Netzen verstehen
7. Fortgeschrittenes maschinelles Lernen mit dem mehrschichtigen Perzeptron
8. Die Sigmoid-Aktivierungsfunktion:Aktivierung in mehrschichtigen neuronalen Perzeptronnetzwerken
9. Wie man ein mehrschichtiges neuronales Perceptron-Netzwerk trainiert
10. Verstehen von Trainingsformeln und Backpropagation für mehrschichtige Perzeptronen
11. Neurale Netzwerkarchitektur für eine Python-Implementierung
12. So erstellen Sie ein mehrschichtiges neuronales Perceptron-Netzwerk in Python
13. Signalverarbeitung mit neuronalen Netzen:Validierung im neuronalen Netzdesign
14. Trainings-Datasets für neuronale Netze:So trainieren und validieren Sie ein neuronales Python-Netz

Was ist ein einschichtiges Perzeptron?

Im vorherigen Artikel haben wir gesehen, dass ein neuronales Netz aus miteinander verbundenen Knoten besteht, die in Schichten angeordnet sind. Die Knoten in der Eingabeschicht verteilen Daten, und die Knoten in anderen Schichten führen eine Summation durch und wenden dann eine Aktivierungsfunktion an. Die Verbindungen zwischen diesen Knoten werden gewichtet, dh jede Verbindung multipliziert das übertragene Datum mit einem Skalarwert.

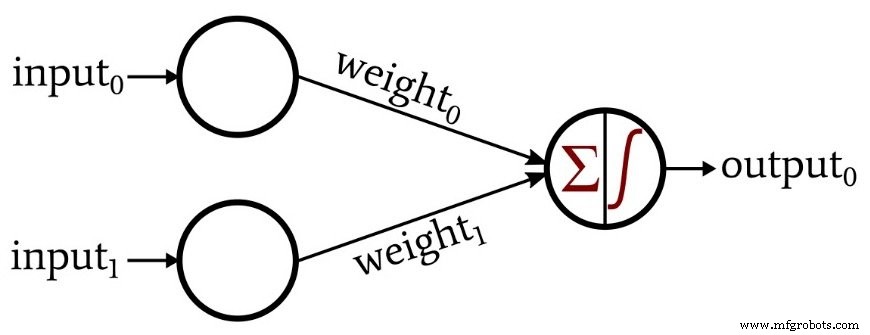
Beachten Sie, dass diese Konfiguration als einschichtiges Perceptron bezeichnet wird. Ja, ich weiß, es hat zwei Schichten (Eingabe und Ausgabe), aber es hat nur eine Schicht, die Rechenknoten enthält.

Klassifizieren mit einem Perzeptron

In diesem Artikel untersuchen wir die Perceptron-Funktionalität mithilfe des folgenden neuronalen Netzwerks.

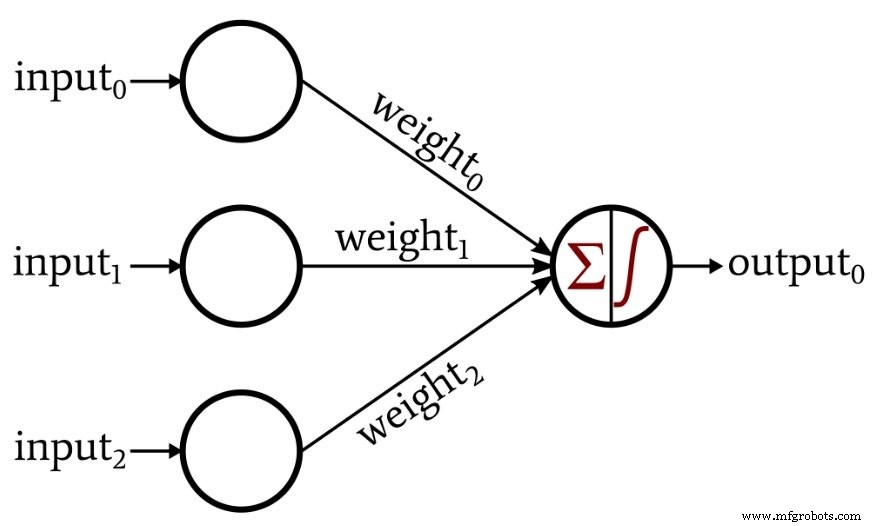
Wie Sie sehen können, ist unsere Eingabedimensionalität drei. Wir können uns dieses Perceptron als Werkzeug zur Lösung von Problemen im dreidimensionalen Raum vorstellen. Lassen Sie uns beispielsweise folgendes Problem vorschlagen:Wenn ein Punkt im dreidimensionalen Raum unterhalb der x-Achse liegt, entspricht er einem ungültigen Datum. Wenn der Punkt auf oder über der x-Achse liegt, entspricht er einem gültigen Datum, das für die weitere Analyse beibehalten werden muss. Wir benötigen dieses neutrale Netzwerk, um unsere Daten zu kategorisieren, wobei ein Ausgabewert von 1 ein gültiges Datum anzeigt und ein Wert von 0 ein ungültiges Datum anzeigt.

Zuerst müssen wir unsere dreidimensionalen Koordinaten auf den Eingabevektor abbilden. Geben Sie in diesem Beispiel₀ . ein ist die x-Komponente, input₁ ist die y-Komponente und input₂ ist die z-Komponente. Als nächstes müssen wir die Gewichte bestimmen. Dieses Beispiel ist so einfach, dass wir das Netzwerk nicht trainieren müssen. Wir können uns einfach die benötigten Gewichte überlegen und zuweisen:

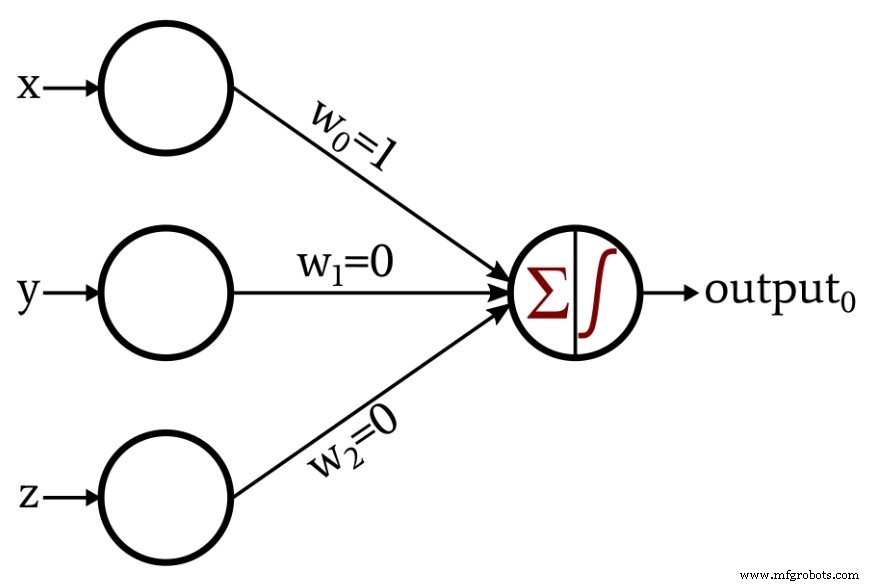
Jetzt müssen wir nur noch angeben, dass die Aktivierungsfunktion des Ausgabeknotens ein Einheitsschritt ist, der wie folgt ausgedrückt wird:

\[f(x)=\begin{cases}0 &x <0\\1 &x \geq 0\end{cases}\]

Das Perceptron funktioniert so:Da w₁ =0 und w₂ =0, die y- und z-Komponenten tragen nicht zur vom Ausgangsknoten erzeugten Summation bei. Das einzige Eingabedatum, das die Summation beeinflusst, ist die x-Komponente, die unverändert an den Ausgabeknoten geliefert wird, da w₀ =1. Wenn der Punkt im dreidimensionalen Raum unter der x-Achse liegt, ist die Summation des Ausgabeknotens negativ und die Aktivierungsfunktion wandelt diesen negativen Wert in Ausgabe₀ . um =0. Wenn der Punkt im dreidimensionalen Raum auf oder über der x-Achse liegt, ist die Summation gleich oder größer Null und die Aktivierungsfunktion wandelt dies in Ausgabe₀ . um =1.

Probleme mit einem Perzeptron lösen

Im vorigen Abschnitt habe ich unser Perceptron als Werkzeug zur Problemlösung beschrieben. Sie haben vielleicht bemerkt, dass das Perceptron nicht viel zur Problemlösung beigetragen hat – ich löste das Problem und gab dem Perceptron die Lösung durch Zuweisen der erforderlichen Gewichte.

An diesem Punkt sind wir bei einem entscheidenden neuronalen Netzkonzept angelangt:Ich konnte das Gültig/Ungültig-Klassifikationsproblem schnell lösen, da der Zusammenhang zwischen den Eingabedaten und den gewünschten Ausgabewerten sehr einfach ist. In vielen Situationen des wirklichen Lebens wäre es jedoch für einen Menschen äußerst schwierig, eine mathematische Beziehung zwischen Eingabedaten und Ausgabewerten zu formulieren. Wir können Eingabedaten erfassen und entsprechende Ausgabewerte aufzeichnen oder erzeugen, aber wir haben keinen mathematischen Weg von der Eingabe zur Ausgabe.

Ein hilfreiches Beispiel ist die Handschrifterkennung. Nehmen wir an, wir haben Bilder von handgeschriebenen Zeichen und möchten diese Bilder als "a", "b", "c" usw. kategorisieren, damit wir Handschrift in normalen Computertext umwandeln können. Jeder, der schreiben und lesen kann, wird in der Lage sein, Eingabebilder zu generieren und dann jedem Bild die richtigen Kategorien zuzuordnen. Somit ist das Sammeln von Eingabedaten und entsprechenden Ausgabedaten nicht schwierig. Andererseits wäre es äußerst schwierig, sich die Eingabe-Ausgabe-Paare anzusehen und einen mathematischen Ausdruck oder Algorithmus zu formulieren, der Eingabebilder korrekt in eine Ausgabekategorie umwandelt.

Somit stellen die Handschrifterkennung und viele andere Signalverarbeitungsaufgaben mathematische Probleme, die der Mensch ohne die Hilfe ausgeklügelter Werkzeuge nicht lösen kann. Trotz der Tatsache, dass neuronale Netze nicht denken, analysieren und innovieren können, ermöglichen sie uns, diese schwierigen Probleme zu lösen, weil sie etwas tun können, was Menschen nicht können – nämlich schnell und wiederholt Berechnungen mit potenziell immensen Mengen numerischer Daten durchführen .

Training des Netzwerks

Der Prozess, der es einem neuronalen Netzwerk ermöglicht, einen mathematischen Pfad von der Eingabe zur Ausgabe zu erstellen, wird als Training bezeichnet. Wir geben dem Netzwerk Trainingsdaten bestehend aus Eingabewerten und entsprechenden Ausgabewerten an, und es wendet ein festes mathematisches Verfahren auf diese Werte an. Ziel dieses Verfahrens ist es, die Gewichte des Netzwerks schrittweise so zu modifizieren, dass das Netzwerk auch mit noch nie dagewesenen Eingangsdaten korrekte Ausgabewerte berechnen kann. Es geht im Wesentlichen darum, Muster in den Trainingsdaten zu finden und Gewichtungen zu generieren, die eine nützliche Ausgabe erzeugen, indem diese Muster auf neue Daten angewendet werden.

Das folgende Diagramm zeigt den oben besprochenen Gültig/Ungültig-Klassifikator, aber die Gewichtungen sind unterschiedlich. Dies sind Gewichte, die ich erzeugt habe, indem ich das Perceptron mit 1000 Datenpunkten trainiert habe. Wie Sie sehen können, hat der Trainingsprozess es dem Perceptron ermöglicht, sich automatisch der mathematischen Beziehung anzunähern, die ich durch kritisches Denken im menschlichen Stil identifiziert habe.

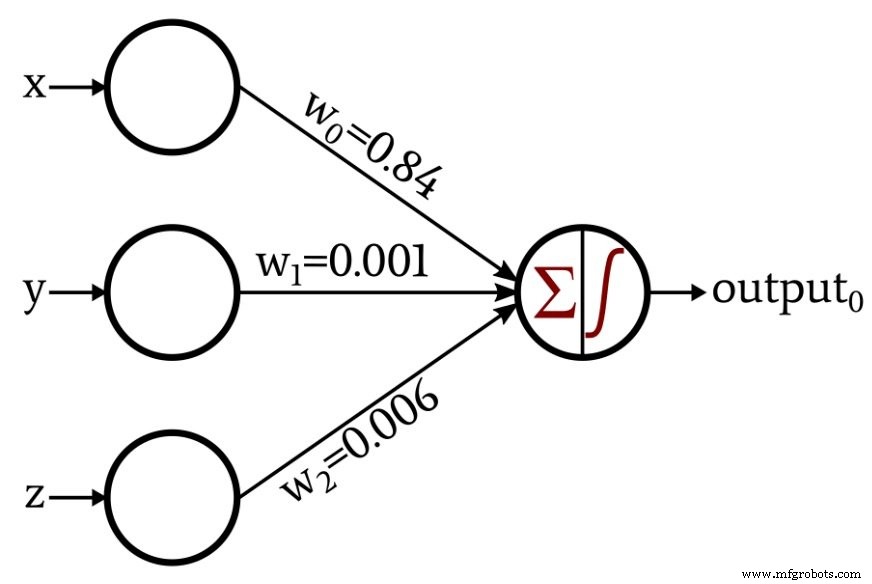
Im nächsten Artikel…

Ich habe Ihnen die Ergebnisse des Trainings dieses Perceptrons gezeigt, aber ich habe nichts darüber gesagt, wie ich diese Ergebnisse erhalten habe. Der nächste Artikel beschreibt ein kurzes Python-Programm, das ein einschichtiges neuronales Perceptron-Netzwerk implementiert, und ich werde auch mein Trainingsverfahren erklären.