Molekulardynamische Modellierung und Simulation des Diamantschneidens von Cer

Hintergrund

Cer (Ce) mit der Ordnungszahl 58 ist eines der am häufigsten vorkommenden Lanthanoidmetalle. Cer hat aufgrund seiner faszinierenden mechanischen, physikalischen und chemischen Eigenschaften breite Anwendungsmöglichkeiten. Es ist bekannt, dass die Morphologie der bearbeiteten Oberflächen von Metallteilen einen starken Einfluss auf deren Funktionalität, Leistung und Lebensdauer hat. Beispielsweise kann die Korrosionsbeständigkeit von Metallteilen effektiv verbessert werden, indem die Oberflächenrauheit verringert oder Druckeigenspannungen in die bearbeitete Oberfläche eingebracht werden [1,2,3]. In jüngerer Zeit haben Yan et al. setzten eine neuartige mechanische Bearbeitungstechnik auf Spitzenbasis ein, um periodische dreieckige Mikrohohlräume auf Cu(111) herzustellen, die nachweislich ein oberflächenverstärktes Raman-Streuungssubstrat sind [4]. Speziell bei Cer, das zur Speicherung von Wasserstoff verwendet wird [5], beeinflusst die Oberflächenbeschaffenheit von Cer stark die Reaktion zwischen Cer und Wasserstoff bei Raumtemperatur. Daher ist das Erreichen einer hohen Genauigkeit der bearbeiteten Oberflächenmorphologie von Cer für seine Anwendungen von entscheidender Bedeutung. Das ultrapräzise Diamantschneiden ist eine wichtige Fertigungstechnik, um eine ultraglatte Oberflächengüte mit hoher Oberflächenintegrität, ultraniedriger Oberflächenrauheit, hoher Ebenheit, geringer metallographischer Strukturentwicklung und geringer Beschädigung unter der Oberfläche zu erzielen [6, 7]. Allerdings wurde selten über experimentelle oder theoretische Arbeiten zum Diamantschneiden von Cer berichtet. Da darüber hinaus beim Ultrapräzisions-Diamant-Schneidprozess der Schneidenradius mit der Schnitttiefe vergleichbar ist, spielen die Eigenschaften des Werkstückmaterials eine wichtige, ja sogar dominante Rolle beim Zerspanungsprozess. Daher ist das Verständnis der Bearbeitungsmechanismen von Cer aufgrund seines komplexen Verformungsverhaltens eine Herausforderung.

Erstens ist Cer für sein außergewöhnlich reichhaltiges Druck-Temperatur-Phasendiagramm bekannt, das durch die Delokalisierung von 4f-Elektronen angetrieben wird. Bei Atmosphärendruck und niedrigen Temperaturen unter 110 K ist das α-Ce (kubisch flächenzentriert (fcc)) stabil. Bei erhöhten Temperaturen im Bereich von 45 bis 275 K wandelt sich das α-Ce in das β-Ce um (doppelt hexagonal dicht gepackt (dhcp)). Das γ-Ce (fcc) ist bei moderaten Temperaturen zwischen 270 und 999 K stabil. Bei hohen Temperaturen zwischen 999 K und der Schmelztemperatur von 1071 K ist das δ-Ce (kubisch raumzentriert (bcc)) stabil [8,9 ,10,11]. Insbesondere die faszinierendste isostrukturelle Phasenumwandlung vom trivalenten γ-Ce niedriger Dichte zum viel dichteren α-Ce bei 295 K und unter 8 kbar wird von einem großen Volumenkollaps von 20 % begleitet [8, 12,13,14 ]. Die phasentransformationsinduzierte Modifikation der elektronischen Struktur und Bindungskonfiguration in Cer hat zwangsläufig einen starken Einfluss auf dessen Verformungsverhalten. Insbesondere die hohe Temperatur und der hohe Druck, die im Kontaktbereich zwischen Schneidwerkzeug und Werkstück entstehen, können beim Diamantschneidprozess zu einer Phasenumwandlung von Cer führen. Zweitens weist metallisches Cer eine beträchtliche Duktilität auf, die durch Versetzungen bestimmt wird [15]. Es ist bekannt, dass Versetzungskeimbildung und Gleiten eine Schlüsselrolle bei der plastischen Verformung von fcc-Metallen unter mechanischer Bearbeitung spielen. Allerdings ist die Wechselwirkung zwischen Phasenumwandlungen und Versetzungen beim Diamantschneiden von Cer noch weitgehend unbekannt.

Die Bestandteile von Bearbeitungsmechanismen bestehen aus dem mikroskopischen Verformungsverhalten des Werkstückmaterials und dessen Korrelation mit makroskopischen Bearbeitungsergebnissen hinsichtlich Schnittkraft, Spanprofil und bearbeiteter Oberflächenmorphologie. Als wichtige Ergänzung zu Bearbeitungsexperimenten hat sich die Molekulardynamik (MD)-Simulation als leistungsfähiges Werkzeug zur Aufklärung grundlegender mechanischer Bearbeitungsmechanismen unterschiedlicher Werkstoffe erwiesen. Liet al. berichteten, dass die minimale Abnutzungstiefe von einkristallinem Cu(111) unter Nanokratzen, die der kritischen Eindringtiefe entspricht, bei der die Plastizität einsetzt, mit dem Sondenradius zunimmt [16]. In jüngerer Zeit untersuchten sie das mechanische Verhalten und die Verformungsmechanismen von AlCrCuFe-Legierungen mit hoher Entropie unter Nanoscratching und berichteten aufgrund der guten Hochtemperaturstabilität des Legierungsmaterials über ein größeres Oberflächenanhäufungsvolumen als reine Metalle [17]. Gaoet al. untersuchten die Entstehung und Entwicklung von Plastizität und Defekten beim orthogonalen Schneiden eines bcc Fe [18]. Zhuet al. berichteten über einen Größeneffekt auf die Sondenformabhängigkeit des Nanokratzens [19]. Hosseiniet al. untersuchten die Auswirkungen des Werkzeugkantenradius auf die Nanobearbeitung von einkristallinem Kupfer [20]. Liuet al. fanden heraus, dass der Unterschied zwischen statischen und dynamischen Reibungskoeffizienten bei der Reibung mit einer einzelnen Unebenheit von Cu(111) aufgrund der Interferenz zwischen Unebenheiten verschwindet [21]. Romero et al. fanden heraus, dass die Adhäsion beim orthogonalen Schneiden eines Kupfersubstrats durch Variation des Spanwinkels und durch die Wahl bestimmter Gitterorientierungen verstärkt werden kann [22]. Yanget al. zeigten, dass die Eigenrotationsgeschwindigkeit und -richtung des Schleifmittels einen signifikanten Einfluss auf die Morphologie und Qualität der bearbeiteten Oberfläche von einkristallinem Kupfer beim Polieren haben [23]. Vargonenet al. berichteten, dass der Spitzenhöhenverlust pro Kratzstrecke beim Kratzen eine Funktion der Normalspannung und des Verjüngungswinkels der Spitze ist [24]. Sonneet al. nachgewiesenen Einfluss von GB auf das Kratzen von bikristallinem Kupfer [25]. Chenet al. fanden heraus, dass Wassermoleküle beim nanometrischen Schneiden von Kupfer die Reibung zwischen Werkzeug und Werkstück effektiv reduzieren [26]. Wuet al. berichteten, dass die Bindungsenergie einen signifikanten Einfluss auf die Reibung hat [27]. Darüber hinaus können die mechanischen Eigenschaften jeder Cerphase im Vergleich zu experimentellen Untersuchungen bequem mittels MD-Simulationen untersucht werden, was für das Verständnis der Wechselwirkung zwischen Phasenumwandlungen und Versetzungen im Cer entscheidend ist. In jüngerer Zeit haben Zhang et al. untersuchten die Wechselwirkungen zwischen Phasenumwandlung und Versetzung am elastisch-plastischen Übergang in Silizium-Nanoindentation durch MD-Simulationen [28]. Nach unserem besten Wissen gibt es jedoch keine Arbeit über die MD-Untersuchung der mechanischen Zerspanung von Cer.

Daher erstellen wir in der vorliegenden Arbeit zunächst das MD-Modell des Diamantschneidens von Cer, indem wir atomare Konfigurationen von Werkstück und Werkzeug konstruieren, empirische Potentiale für Ce-Ce- und Ce-C-Atomwechselwirkungen zuweisen und zwei fcc-Phasen von Cer charakterisieren. Mit dem etablierten MD-Modell führen wir dann MD-Simulationen zum Diamantschneiden von Cer durch, um die grundlegenden Bearbeitungsmechanismen von Cer aufzuklären und die Einflüsse des Spanwinkels des Schneidwerkzeugs und der kristallographischen Orientierung des Werkstücks auf den Schneidprozess zu untersuchen.

Methoden

MD-Modell des Diamantschneidens

Abbildung 1 zeigt das MD-Modell des Diamantschneidens, das aus einem einkristallinen Cer-Werkstück und einem Diamant-Schneidwerkzeug besteht. Das Cer-Werkstück hat eine Abmessung von 41, 25 und 31 nm in horizontaler, vertikaler bzw. Längsrichtung und besteht aus einer Million γ-Ce-Atomen in fcc-Struktur. Periodische Randbedingung wird nur in Längsrichtung angewendet. Das Werkstück besteht aus zwei Arten von Atomen, jeweils als Bodenatome und bewegliche Atome. Die Schicht der unteren Atome mit einer Dicke von 2 nm ist im Raum fixiert, um eine starre Bewegung des Werkstücks zu verhindern. Die Bewegung beweglicher Atome folgt der Newtonschen Bewegungsgleichung mit einem Geschwindigkeits-Verlet-Integrationsalgorithmus. Die Temperatur jedes Atoms im Werkstück wird während des Schneidprozesses überwacht, um die erzeugte Wärmeableitung darzustellen. Um den Einfluss der kristallographischen Orientierung zu berücksichtigen, werden drei Cer-Werkstücke mit (010), (110) und (111) freier Oberfläche in vertikaler Richtung betrachtet. Das Diamant-Schneidwerkzeug mit scharfer Schneide hat einen Freiwinkel von 9° und besteht aus 0,1 Millionen C-Atomen in Diamantstruktur. Sieben Spanwinkel als –30°, –20°, –10°, 0°, 10°, 20° und 30° werden verwendet, um den Einfluss des Spanwinkels zu berücksichtigen. Angesichts der ultrahohen Härte von Diamant im Vergleich zu Cer und des ultrakurzen Schnittweges wird der Verschleiß des Diamantwerkzeugs während des Schneidprozesses nicht berücksichtigt. Daher wird das Diamantschneidwerkzeug als starrer Körper eingestellt, dh die Koordinaten und Geschwindigkeiten aller Atome im Schneidwerkzeug werden bei jedem Schritt aktualisiert, so dass sich das Schneidwerkzeug als eine Einheit ohne Verformung bewegt.

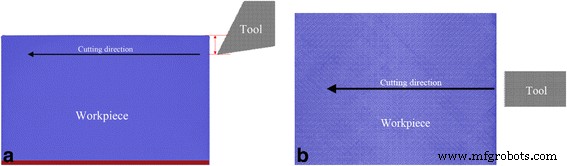
MD-Modell zum Diamantschneiden von Cer; (Farbe online) MD-Modell zum Diamantschneiden von Cer. a Vorderansicht und b Draufsicht . Rot und blaue Farben stehen für untere und bewegliche Ce-Atome und graue Farbe zeigt C-Atome an

Es gibt drei Arten von atomaren Wechselwirkungen im simulierten System, als Ce-Ce im Cer-Werkstück, Ce-C zwischen dem Cer-Werkstück und dem Diamant-Schneidwerkzeug bzw. C-C im Diamant-Schneidwerkzeug. Die C-C-Wechselwirkungen entfallen, da das Diamant-Schneidwerkzeug als starrer Körper ohne Verformung im Schneidprozess behandelt wird. Die Methode der eingebetteten Atome (EAM), die aus wechselwirkendem Paarpotential und Elektroneneinbettungsenergie besteht, wurde häufig verwendet, um metallische Systeme zu beschreiben, die ausgedrückt werden kann als

wo r _ij ist der Abstand zwischen den Atomen i und j , ϕ _ij ist das Paarpotential zwischen Atomen i und j , F _ich stellt die Einbettungsenergie dar, die erzeugt wird, wenn ein Atom i eingebettet ist, ρ _ich ist die Elektronendichte bei i Atom erzeugt von allen Atomen außer Atom i , und ρ _j ist eine Funktion der Elektronendichte des Atoms j am Atom i . Die EAM-Parameter für Cer von Sheng et al. werden verwendet, um die Ce-Ce-Wechselwirkungen zu beschreiben, die in der Lage sind, volumenelastische Eigenschaften von fcc-Cer-Phasen genau zu beschreiben [29]. Das Morsepotential wird verwendet, um die Ce-C-Wechselwirkung zu beschreiben, die ausgedrückt werden kann als

wo D ₀ (0,087 eV) ist die Kohäsionsenergie, α (5.14) ist der Elastizitätsmodul und r ₀ (2.93 Å) steht für den Gleichgewichtsabstand zwischen den Atomen i und j , bzw. Der Grenzradius des Morsepotentials wird als 1,0 nm [30] gewählt.

Das so erstellte Simulationssystem wird zunächst auf seine Gleichgewichtskonfiguration bei 30 K und unter 0 bar im NPT-Ensemble äquilibriert (konstante Anzahl von Atomen N , konstanter Druck P , und konstante Temperatur T ). Anschließend wird das äquilibrierte Werkstück mit einer konstanten Geschwindigkeit von 100 m/s und einer Schnitttiefe von 4 nm im kanonischen Ensemble (konstante Atomzahl N , konstantes Volumen V , und konstante Temperatur T ). Die Schnittrichtung wird durch rot eingefärbte Pfeile in verschiedenen Ansichten des Schnittmodells angezeigt. Und die Schnittkraft ist als Kraftkomponente entlang der Schnittrichtung definiert. Die genutzte Schnitttiefe im Ultrapräzisions-Bearbeitungsexperiment beträgt wenige Mikrometer. Wir stellen fest, dass die simulierten Abmessungen des Werkstücks und die Schnitttiefe aufgrund der Begrenzung der Längenskala bei atomistischen Simulationen um mehrere Größenordnungen kleiner sind als die, die in Experimenten zum ultrapräzisen Diamantschneiden verwendet werden. Wir stellen auch fest, dass die verwendete Schnittgeschwindigkeit von 100 m/s in aktuellen MD-Simulationen des nanometrischen Schneidens um mehrere Größenordnungen höher ist als die typischen Geschwindigkeiten von mehreren zehn Mikrometern pro Sekunde, die in Ultrapräzisions-Diamantschneidexperimenten verwendet werden, was die intrinsische Anforderung der Integrationszeitschritt in der Größenordnung von Femtosekunden (fs). Die Common Neighbor Analysis (CNA) wird verwendet, um Typen von Gitterdefekten zu identifizieren [31] und das Farbschema ist wie folgt:Grün steht für fcc-Atome, Rot für hexagonal dicht gepackte (hcp) Atome, Blau für kubisch-raumzentrierte (bcc) Atome und grau für andere Atome, einschließlich Oberflächenatome und Versetzungskerne. Alle MD-Simulationen werden unter Verwendung des LAMMPS-Codes mit einem Integrationszeitschritt von 1 fs durchgeführt [32]. Und OVITO wird verwendet, um MD-Daten zu visualisieren und MD-Snapshots zu erstellen [33].

Charakterisierung von Cer-Phasen

In der vorliegenden Arbeit werden fünf Cerphasen als γ, α, β, ε bzw. δ betrachtet. Tabelle 1 listet die Strukturparameter und die zugehörigen Temperatur-Druck-Bedingungen für jede Phase auf, die aus der Literatur [8,9,10,11] zusammengetragen wurden. Die atomare Massenkonfiguration jeder Phase wird dann gemäß Tabelle 1 konstruiert. Anschließend werden rechnerische Simulationen von einachsiger Spannung, Scherung und gleichförmiger Kompression von wie konstruierten Massenkonfigurationen durchgeführt, um die mechanischen Eigenschaften verschiedener Ce-Phasen abzuleiten. Aufgrund der hohen stabilen Temperatur nahe dem Schmelzpunkt von Cer werden die mechanischen Eigenschaften des δ-Ce nicht berechnet, da es schwierig ist, mechanische Tests an der flüssigen Phase durchzuführen. Tabelle 2 listet die abgeleiteten elastischen Konstanten und mechanischen Eigenschaften jeder Cerphase auf. Der berechnete Young-Modul der einkristallinen γ-Ce-Phase beträgt 24,17 GPa, was mit dem experimentellen Wert von 36,7 GPa vergleichbar ist, der bei der Nanoindentation seines polykristallinen Gegenstücks berichtet wurde [10]. Darüber hinaus unterscheiden sich die berechneten Werte von C44 und 1/2(c11-c12) um den Faktor 3, was gut mit den experimentellen Werten bei Verwendung von Techniken der inelastischen Neutronenstreuung übereinstimmt [34]. Tabelle 2 zeigt, dass das dichtere α-Ce im Vergleich zu seiner isostrukturellen γ-Ce-Phase niedriger Dichte deutlich verbesserte mechanische Eigenschaften aufweist.

Die radiale Verteilungsfunktion (RDF), definiert als Dichtevariationen in einem Partikelsystem mit dem Abstand von einem Referenzpartikel in Form von scharfen Peaks. Der RDF kann aus Röntgenspektren und Neutronenbeugungsdaten abgeleitet werden [35, 36]. Daher ist es eines der wichtigsten Werkzeuge zur strukturellen Charakterisierung von Flüssigkeiten und Festkörpern und fungiert als wichtiges Bindeglied zwischen mikroskopischen Atomanordnungen und makroskopischen Eigenschaften. In der aktuellen Studie wird das RDF verwendet, um strukturelle Unterschiede zwischen verschiedenen Cerphasen zu charakterisieren. Abbildung 2a stellt die RDF-Histogramme für die fünf Cer-Phasen dar, in denen Peaks Charakteristiken der entsprechenden Gitterstruktur darstellen:der erste, zweite und drittnächste Nachbarabstand von γ-Ce beträgt 3,64, 5,13 bzw. 6,3 Å; der erste, zweite und drittnächste Nachbarabstand von α-Ce beträgt 3,41, 4,85 bzw. 5,92 Å; der erste und der zweitnächste Nachbarabstand von δ-Ce beträgt 3,53 bzw. 6,75 Å; der erste, zweite, dritte und vierte nächste Nachbarabstand von ε-Ce beträgt 2,96, 3,33, 4,91 bzw. 5,69 Å; der erste, zweite, dritte und viertnächste Nachbarabstand von β-Ce beträgt 3,71, 3,97, 5,27 bzw. 5,92 Å. Um die Durchführbarkeit der Vorhersage von Phasenumwandlungen zwischen zwei fcc-Cer-Phasen durch die verwendeten EAM-Potentialparameter zu demonstrieren, wird die gleichmäßige Kompression des Bulk-γ-Ce bis zum Erreichen eines Volumenkollapses von 20 % durchgeführt. Abbildung 2b zeigt die RDF vor und nach der Kompression, die jeweils gut mit der RDF von γ-Ce und α-Ce übereinstimmt, was das Auftreten der bekanntesten γ ➔ α-Phasentransformation anzeigt [12,13,14] .

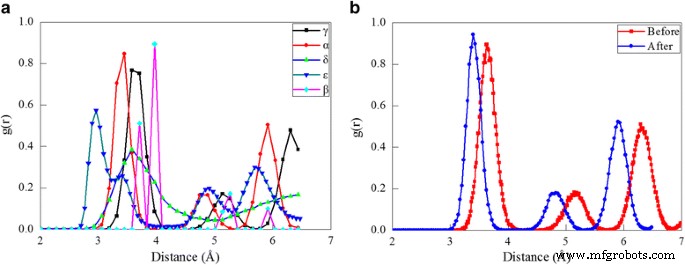
RDF-Analyse von Cer-Phasen; (Farbe online) a RDF von Cer-Phasen. b RDF vor und nach der Komprimierung des γ-Ce

Ergebnisse und Diskussion

Bearbeitungsmechanismen von Cer

Zunächst wird eine MD-Simulation des Diamantschneidens von Ce(010) durchgeführt, um die grundlegenden Bearbeitungsmechanismen von Cer aufzuklären. Das verwendete Diamantschneidwerkzeug hat einen Spanwinkel von 0°. Es gibt drei Komponenten der Bearbeitungskraft, nämlich Schnittkraft in horizontaler Richtung, Normalkraft senkrecht zur bearbeiteten Oberfläche und Querkraft in Längsrichtung. Bild 3 zeigt den Verlauf von Schnittkraft und Normalkraft mit der Schnittlänge während des Schnittprozesses, die nach Schnittlänge in drei Zonen eingeteilt werden. Dementsprechend zeigt die Unterfigur in jeder Zone eine repräsentative Schnittkonfiguration, in der Atome entsprechend ihren CNA-Werten gefärbt sind und fcc-Atome zur klaren Visualisierung von Defekten nicht gezeigt werden.

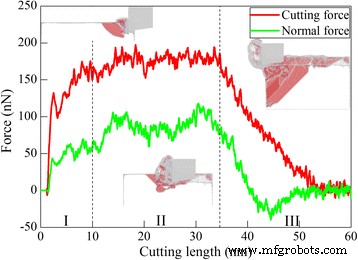
Variation der Bearbeitungskraft; (Farbe online) Variation von Schnittkraft und Normalkraft mit der Schnittlänge beim Diamantschneiden von Ce(010) unter einem Spanwinkel von 0°. Teilabbildungen zeigen repräsentative Defektkonfigurationen in verschiedenen Zonen, in denen Atome entsprechend ihren CNA-Werten gefärbt sind

Aus Fig. 3 ist ersichtlich, dass sowohl die Schnittkraft als auch die Normalkraft aufgrund der Adhäsion zwischen Schneidwerkzeug und Werkstück negative Werte haben, wenn das Schneidwerkzeug dicht am Werkstück ist. Wenn das Schneidwerkzeug mit dem Werkstück in Berührung kommt, wird das Material zunächst elastisch verformt, wobei sowohl die Schnittkraft als auch die Normalkraft schnell ansteigen. Abbildung 3 zeigt, dass sowohl die Schnittkraft als auch die Normalkraft bei einer Schnittlänge von 2,3 nm schnell abfallen, was auf den Beginn der plastischen Verformung hinweist. Beim weiteren Schneiden steigen sowohl die Schnittkraft als auch die Normalkraft mit starken Schwankungen, die durch aufeinanderfolgende Nukleationsereignisse verursacht werden. Aus der Unterfigur in Zone II ist ersichtlich, dass in der Nähe der Schneidzone beträchtliche 1/6 112 -Shockley-Teilversetzungen erzeugt werden. Sowohl Schnittkraft als auch Normalkraft schwanken hauptsächlich um konstante Werte in der Schnittlänge im Bereich von 10 bis 35 nm, was auf einen stabilen Schnittprozess hindeutet. Und Versetzungen in Zone II befinden sich hauptsächlich sowohl vor als auch unter dem Diamantschneidwerkzeug. Wenn die Schnittlänge 35 nm erreicht, beginnt sich das Schneidwerkzeug vom Werkstück zu lösen, was mit einem deutlichen Abfall sowohl der Schnittkraft als auch der Normalkraft einhergeht. Die Unterfigur in Zone III zeigt deutliche Versetzungen, die von der linken Seite des Werkstücks blockiert werden. Sowohl die Schnittkraft als auch die Normalkraft werden stabil, bis der gebildete Span vollständig vom Werkstück getrennt ist. Abbildung 3 zeigt, dass die Normalkraft während des Schneidvorgangs geringer ist als die Schneidkraft.

Abbildung 4a–d zeigt augenblickliche Fehlerstrukturen innerhalb des Werkstücks bei unterschiedlichen Schnittlängen. Atome sind entsprechend ihren CNA-Werten gefärbt, und fcc-Atome werden nicht gezeigt. Dementsprechend zeigen Abb. 4e–h bearbeitete Oberflächenmorphologien, die durch ihre Atomhöhen gefärbt sind. Die dynamische Untersuchung der Defektentwicklung zeigt, dass das Nachgeben des Werkstücks von einer Keimbildung von 1/6<112>-Shockley-Teilversetzungen von der rechten freien Oberfläche und ihrem anschließenden Gleiten auf benachbarten {111}-Gleitebenen und entlang <110>-Gleitrichtungen begleitet wird. Die Bewegung von Shockley-Teilversetzungen wird von einer Ausdehnung von Stapelfehlern begleitet, die von Versetzungskernen begrenzt werden. Mit dem Fortschreiten des Schneidprozesses emittiert eine große Menge partieller Versetzungen von der oberen freien Oberfläche vor dem Schneidwerkzeug, was zu beträchtlichen Spänen führt, die entlang der Spanfläche des Schneidwerkzeugs gebildet werden, wie in 4f gezeigt. Gleichzeitig bewegen sich Versetzungen hinter dem Schneidwerkzeug nach oben, um an der oberen freien Oberfläche zu vernichten, was zu einer signifikanten Erholung der bearbeiteten Oberfläche führt. Fig. 4c zeigt, dass, wenn sich das Schneidwerkzeug der linken Grenze des Werkstücks nähert, die Ausbreitung von Versetzungen durch die linke freie Oberfläche stark blockiert wird, begleitet von einem deutlich erhöhten Spanvolumen, wie in Fig. 4g gezeigt. Abbildung 4d zeigt, dass nach der vollständigen Trennung zwischen Span und Werkstück die Versetzungsdichte innerhalb des Werkstücks aufgrund der Versetzungsvernichtung an der oberen freien Oberfläche deutlich abnimmt.

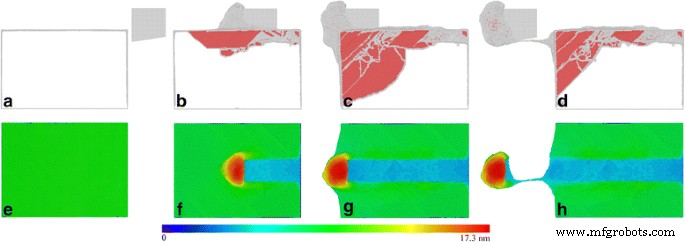
Defektstrukturen und bearbeitete Oberflächenmorphologien; (Farbe online) MD-Schnappschüsse von momentanen Defektstrukturen (obere Reihe ) und bearbeitete Oberflächenmorphologie (untere Reihe ) beim Diamantschneiden von Ce(010) unter einem Spanwinkel von 0°. Schnittlängen:a , e 0,0 nm, b , f 18,8 nm, c , g 44,8 nm und d , h 59,6 nm. Atome in der oberen Reihe und untere Reihe sind entsprechend ihrer CNA-Werte bzw. Atomhöhen eingefärbt

Neben der durch Versetzungsschlupf dominierten Plastizität wird die Wahrscheinlichkeit der Phasenumwandlung beim Diamantschneidprozess auch durch eine RDF-Analyse der Defektzone innerhalb des Werkstücks und der gebildeten Späne bewertet. Das γ-Ce in der fcc-Struktur wird zuerst in OVITO unter Verwendung des CNA-Algorithmus ausgeschlossen, und die restlichen Atome bestehen aus Defektzonen einschließlich bcc, hcp und anderen Atomen. Dann wird eine RDF-Analyse an der Defektzone durchgeführt. Und die Menge der verschiedenen Ce-Phasen kann aus der Anzahl verschiedener Arten von Defektatomen abgeleitet werden. Abbildung 5a zeigt, dass die drei Peaks des RDF der Defektzone unter der bearbeiteten Oberfläche gut mit den genauen drei Peaks des RDF des δ-Ce übereinstimmen, was auf das Auftreten einer Phasenumwandlung von γ-Ce zu δ-Ce hindeutet. Während δ-Ce bei hoher Temperatur und niedrigem Druck stabil ist, weist die aufgetretene γ ➔ δ-Phasentransformation auf die hohe Wärmeableitung hin, die beim Schneidprozess erzeugt wird. Da außerdem das δ-Ce andere mechanische Eigenschaften aufweist als die γ-Ce-Phase, führt das erzeugte δ-Ce zu einer heterogenen Bearbeitung im nachfolgenden Schneidprozess. Abbildung 5b zeigt, dass in den geformten Spänen auch δ-Ce-Atome nachgewiesen werden, hauptsächlich aufgrund der durch hohe Temperatur ausgelösten γ ➔ δ-Phasentransformation im Kontaktbereich zwischen dem geformten Span und der Spanfläche des Schneidwerkzeugs. Die Menge an gebildetem δ-Ce sowohl in der Defektzone als auch im Span ist jedoch sehr trivial, was darauf hindeutet, dass die Phasenumwandlung beim Diamantschneiden von Cer nicht ausgeprägt ist.

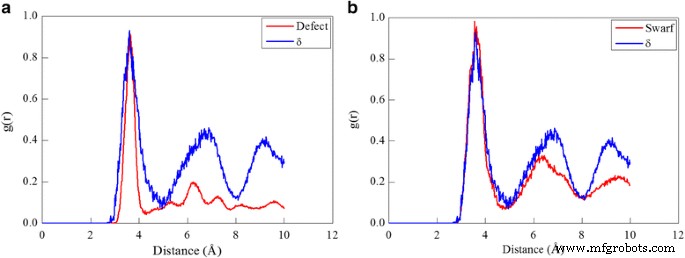
Analyse der Phasenumwandlung im Schneidprozess; (Farbe online) Analyse der Phasenumwandlung beim Diamantschneiden von Ce(010) unter einem Spanwinkel von 0°. RDF von a Werkstück und b Späne nach dem Schneiden

Einfluss des Spanwinkels

Mit dem grundlegenden Verständnis der Zerspanungsmechanismen von Cer wird der Einfluss des Spanwinkels des Schneidwerkzeugs auf die Diamantzerspanung untersucht. Abbildung 6 zeigt gemittelte Werte sowohl der Schnittkraft als auch der Normalkraft für die sieben Spanwinkel. Der Durchschnittswert jeder Kraftkomponente wird durch Mittelung der Momentankraftwerte in der Schnittlänge im Bereich von 10 bis 35 nm berechnet. Abbildung 6 zeigt, dass die Schnittkraft für jeden Spanwinkel höher als die Normalkraft ist. Allerdings ist der Differenzwert der beiden Kraftkomponenten bei größeren Spanwinkeln ausgeprägter. Außerdem nehmen sowohl die Schnittkraft als auch die Normalkraft mit zunehmendem Spanwinkel ab. Nach der Theorie des Händlers nimmt mit zunehmendem Spanwinkel auch der der Mindestenergie entsprechende Scherebenenwinkel zu, was entsprechend die Schnittkraft senkt [37]. Die durch aktuelle MD-Simulationen aufgezeigte Spanwinkel-abhängige Bearbeitungskraftvariation stimmt gut mit der Theorie des Händlers überein.

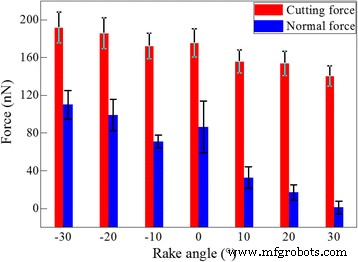
Spanwinkelabhängigkeit der Bearbeitungskraft; (Farbe online) Einfluss des Spanwinkels auf die Bearbeitungskraft

Abbildung 7a, b zeigt eine Unteransicht der Defektstruktur unter der bearbeiteten Oberfläche nach Abschluss des Diamantschneidprozesses mit einem Spanwinkel von –30° bzw. 30°. Für jeden Spanwinkel sind beide Versetzungstypen und die Geometrie der Versetzung in Bezug auf die freie Oberfläche gleich. Allerdings ist die Versetzungsdichte für den Spanwinkel von –30° signifikant höher als für den Spanwinkel von 30°, was darauf hindeutet, dass eine komplexere plastische Verformung aufgetreten ist. Abbildung 7c zeigt die Anzahl der im Werkstück verbliebenen Versetzungssegmente nach dem Diamantschneiden mit unterschiedlichen Spanwinkeln, was darauf hinweist, dass die Versetzungsdichte mit zunehmendem Spanwinkel abnimmt. Es sollte beachtet werden, dass verschiedene Arten von Luxationen, die durch die Burgers-Vektoren kategorisiert werden, einschließlich 1/2<110> perfekte Luxation, 1/6<112> teilweise Shockley-Dislokation, 1/6<110> Stair-Rod-Dislokation und 1/3 <111> Frank partielle Dislokation, sind in Fig. 7c berücksichtigt. Bei nanometrischen Schneidprozessen korreliert die versetzungsvermittelte mikroskopische Verformung des Werkstückmaterials in Bezug auf die Bearbeitungskraft und die bearbeitete Oberflächenmorphologie stark mit den makroskopischen Bearbeitungsergebnissen. Zum Beispiel führt die Wechselwirkung und Reaktion von Versetzungen zur Bildung von sessilen Versetzungsstrukturen, die die nachfolgende Versetzungsbewegung blockieren; folglich führt die resultierende Kaltverfestigung zu einer Erhöhung der Bearbeitungskraft. Die Vernichtung von Versetzungen an der freien Oberfläche führt zur Erholung der bearbeiteten Oberfläche, begleitet von der Bildung von Oberflächenanhäufungen [38].

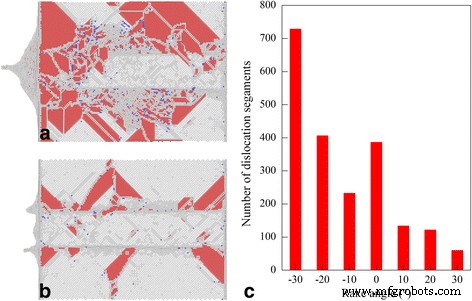
Defektstrukturen erzeugt mit unterschiedlichen Spanwinkeln; (Farbe online) MD-Schnappschüsse von Defektstrukturen nach dem Schneiden von Cer mit einem Spanwinkel von a −30° und b 30°. Atome werden entsprechend ihren CNA-Werten gefärbt. c Spanwinkelabhängige Versetzungszahl

Abbildung 8 zeigt bearbeitete Oberflächenmorphologien nach Abschluss der Schneidprozesse für verschiedene Spanwinkel. Das Volumen der Flächenanhäufungen auf beiden Seiten der geformten Nut ist für den Spanwinkel bei negativen Werten ausgeprägter als bei positiven Werten. Außerdem ist die Verteilung der Oberflächenstapelung bei negativem Spanwinkel weniger gleichmäßig als bei positivem Spanwinkel. Abbildung 8c zeigt deutlich die Asymmetrieverteilung der Oberflächenstapelung entlang der geformten Nut für den Spanwinkel von –30°. Aus Fig. 8 ist ersichtlich, dass das Volumen der Oberflächenanhäufung mit zunehmendem Spanwinkel abnimmt. Daher wird angegeben, dass der Spanwinkel von 30° optimal für das Diamantschneiden von Cer für die niedrigste Bearbeitungskraft, die niedrigste Versetzungsdichte und den niedrigsten Oberflächenaufbau als die anderen Spanwinkel ist.

Spanwinkelabhängigkeit der bearbeiteten Oberflächenmorphologien; (Farbe online) bearbeitete Oberflächenmorphologie mit verschiedenen Spanwinkeln:a −10°, b −20°, c −30°, d 10°, e 20° und f 30°. Atome werden entsprechend ihrer Atomhöhe gefärbt

Einfluss der Kristallorientierung des Cer-Werkstücks

Der Einfluss der Kristallorientierung auf das Diamantschneiden von Cer unter dem optimalen Spanwinkel von 30° wird ebenfalls untersucht. Alle Bearbeitungsparameter sind für Ce(010), Ce(110) und Ce(111) gleich. Abbildung 9 zeigt Variationen von Schnittkraft und Versetzungszahl bei unterschiedlichen Kristallorientierungen. Die Schnittkraft von Ce(010) ist deutlich geringer als die von Ce(110) und Ce(111). Obwohl die Versetzungszahl in Ce(111) am niedrigsten ist, ist die Versetzungsdichte in Ce(010) deutlich geringer als die in Ce(110). Es ist bekannt, dass die Geometrie zwischen Gleitebene und freier Oberfläche mit der Kristallorientierung variiert. Sowohl für Ce(010) als auch für Ce(110) sind die vier {111}-Gleitebenen zur bearbeiteten Oberfläche geneigt. Es gibt jedoch eine {111} Gleitebene parallel zur bearbeiteten Oberfläche von Ce(111), zusätzlich zu drei {111} geneigten Gleitebenen. While microscopic deformation of workpiece material is dominated by dislocation slips, the observed macroscopic machining results in terms of machined surface and machining force can also be influenced by machined surface morphology. Although the easy glide of dislocations on the {111} slip plane parallel to free surface is energetically favorable for the accommodation of plastic strain caused by cutting tool action, the resulting considerable surface pile up increases the machining resistance, which leads to a high cutting force.

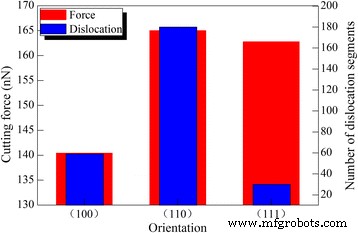
Crystal orientation dependence of cutting force and dislocation number; (color online) crystal orientation dependence of cutting force and dislocation number

Figure 10a–c presents machined surface morphology of Ce(010), Ce(110), and Ce(111), respectively, indicating that the crystal orientation has a strong influence on machined surface quality. The volume of surface pile up is the smallest for Ce(010), followed by Ce(111), and the largest for Ce(110). Correspondingly, the material removal in the form of chip is the most pronounced for Ce(010). Furthermore, it is seen that the surface pile up of Ce(111) on both side of formed groove presents the highest symmetry, while that of Ce(110) is the worst. Therefore, it is indicated that the crystal orientation of (010) is optimal for the diamond cutting of cerium due to its low machining force, low dislocation density, and low surface pile up.

Crystal orientation dependence of machined surface morphology; (color online) crystal orientation dependence of machined surface morphology. Atoms are colored according to atomic heights. Crystal orientation. a (010). b (110). c (111)

Schlussfolgerungen

In summary, we perform MD modeling and simulation to elucidate the underlying mechanisms of cerium under the ultra-precision diamond cutting. The EAM and Morse potentials are respectively employed to describe atomic interactions within cerium workpiece and the interactions between cerium workpiece and diamond cutting tool. The elastic constants, mechanical properties, and propensity of phase transformation of cerium phases are evaluated, which demonstrates the feasibility of predicting phase transformation of cerium by the current established MD model. Subsequent MD simulations of diamond cutting reveal that the plastic deformation of cerium is governed by dislocation nucleation and subsequent glide, which is similar with other fcc metals. In addition, there is γ ➔ δ phase transformation occurred within both machined surface and formed chip. It is found that high quality of machined surface and low machining force can be achieved in the diamond cutting of cerium with the optimal machining conditions, i.e., a rake angle of 30° for a crystal orientation of (010).