Was ist die Fourier-Transformation?

Dieser Artikel gibt Ihnen wesentliche Informationen zu einer mathematischen Technik, die eine absolut grundlegende Rolle beim Systemdesign und der Signalverarbeitung spielt.

Die Fourier-Transformation wurde nach dem französischen Mathematiker Joseph Fourier benannt und ist ein mathematisches Verfahren, mit dem wir den Frequenzgehalt bestimmen können einer Funktion. Für Elektroingenieure wird die Fourier-Transformation normalerweise auf Zeitfunktionen angewendet, die wir Signale nennen .

Sinusförmige Zerlegung

Ein Diagramm von Spannung oder Strom über der Zeit, wie wir es auf einem Oszilloskop-Display sehen würden, ist eine intuitive Darstellung des Signalverhaltens. Es ist jedoch nicht die einzige nützliche Darstellung.

In vielen Fällen – zum Beispiel beim Design von HF-Systemen – interessiert uns vor allem das periodische Verhalten von Signalen. Genauer gesagt sind wir daran interessiert, ein Signal in Bezug auf sinusförmige . zu verstehen Periodizität, weil Sinuskurven der einzigartige mathematische Ausdruck der „reinen“ Frequenz sind.

Die Fourier-Transformation zeigt die elementare Periodizität eines Signals durch Zerlegung das Signal in seine konstituierenden Sinusfrequenzen und Identifizieren der Größen und Phasen dieser konstituierenden Frequenzen.

Das Wort „Zersetzung“ ist hier entscheidend. Die Fourier-Transformation lehrt uns, ein Zeitbereichssignal als eine Wellenform zu betrachten, die besteht aus zugrundeliegende sinusförmige Wellenformen mit verschiedenen Größen und Phasen.

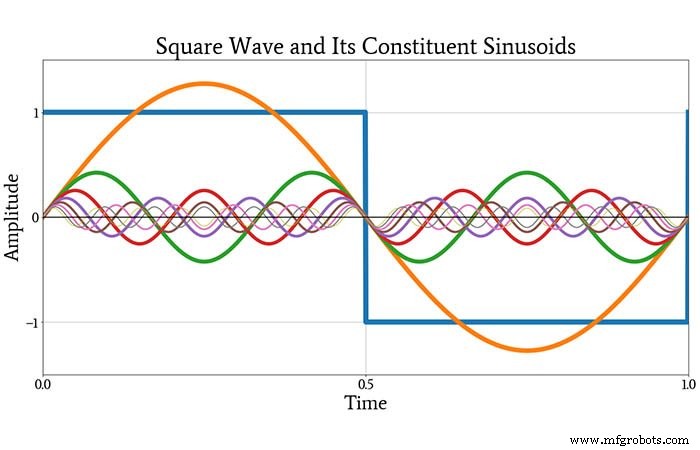
Eine Rechteckwelle zum Beispiel kann in eine unendliche Reihe von Sinuskurven mit stetig abnehmenden Amplituden und stetig ansteigenden Frequenzen zerlegt werden. Die genaue Reihe für eine AC-gekoppelte Rechteckwelle der Periode T und der Amplitude A kann wie folgt geschrieben werden:

\[f_{square}(t)=\frac{4A}{\pi}\sum_{k\in{\{1,3,5,...\ }}}\frac{1}{k}\sin\left(\frac{2\pi kt}{T}\right)\]

Wir können dies in die folgende Form umwandeln, die etwas intuitiver ist:

\[f_{square}(t)=\frac{4A}{\pi}\left(\sin(2\pi ft)+\frac{1}{3 }\sin(6\pi ft)+\frac{1}{5}\sin(10\pi ft)+\ ...\right)\]

wobei f die Frequenz der Rechteckwelle in Hertz ist.

Das folgende Diagramm zeigt die ursprüngliche Rechteckwelle in Blau und die ersten acht Sinuskurven in der unendlichen Reihe.

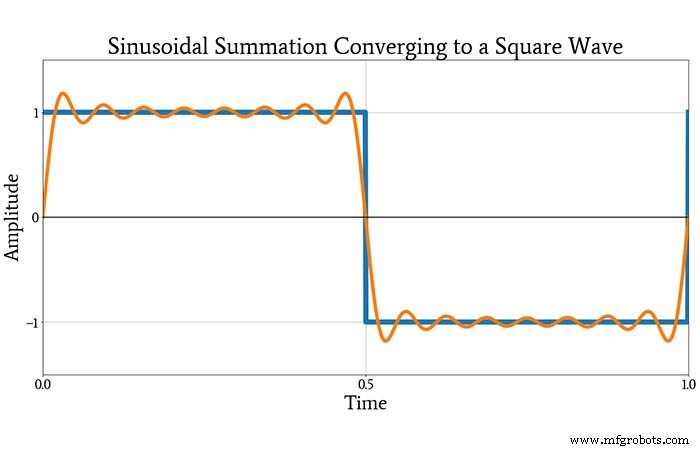
Nachdem Sie sich dieses Diagramm angesehen haben, sind Sie vielleicht immer noch etwas skeptisch, ob diese Sinuskurven zu einer Rechteckwelle kombiniert werden können. Der nächste Plot wird Sie jedoch überzeugen. Es zeigt die ursprüngliche Rechteckwelle und die durch Hinzufügen erzeugte Wellenform alle oben gezeigten konstituierenden Sinuskurven.

Funktionen von Zeit und Häufigkeit

Wenn wir eine Fourier-Transformation berechnen, beginnen wir mit einer Zeitfunktion f(t) und erzeugen durch mathematische Zerlegung eine Frequenzfunktion F(ω). (In theoretischen Diskussionen über die Fourier-Transformation verwenden wir normalerweise die Winkelfrequenz.)

Die Auswertung von F(ω) bei einer bestimmten Winkelfrequenz, sagen wir 100 rad/s, liefert uns die Größe und Phase der sinusförmigen Komponente von f(t), die eine Frequenz von 100 rad/s hat. Wenn f(t) keine sinusförmige Komponente bei 100 rad/s hat, ist der Betrag null.

Sie fragen sich vielleicht, wie eine Funktion, F(ω), sowohl Betrag als auch Phase ausgeben kann. Die Fourier-Transformation erzeugt ein komplexwertiges Funktion, was bedeutet, dass die Transformation selbst weder der Betrag der Frequenzkomponenten in f(t) noch die Phase dieser Komponenten ist. Wie bei jeder komplexen Zahl müssen wir zusätzliche Berechnungen durchführen, um den Betrag oder die Phase zu extrahieren.

Das Konzept einer komplexwertigen Transformation ist etwas intuitiver, wenn wir mit einer diskreten arbeiten Fourier-Transformation anstelle einer „Standard“-Transformation, bei der wir mit einer symbolischen Funktion der Zeit beginnen und mit einer symbolischen Funktion der Frequenz enden.

Die diskrete Fourier-Transformation arbeitet mit einer Folge numerischer Werte und erzeugt eine Folge von Fourier-Koeffizienten . Diese Koeffizienten sind typische komplexe Zahlen (d. h. sie haben die Form a + jb), und wir verwenden normalerweise den Betrag dieser komplexen Zahlen, berechnet als √(a ² +b ² ), wenn der Frequenzinhalt eines Signals analysiert wird.

Aufzeichnen der Fourier-Transformation

Darstellungen des Frequenzinhalts sind in Datenblättern, Testberichten, Lehrbüchern usw. sehr verbreitet. Wir bezeichnen ein Diagramm der Größe über der Frequenz oft als Spektrum – zum Beispiel „Schauen wir uns das Spektrum des Signals an“ bedeutet „sehen wir uns eine Art visuelle Darstellung der Größeninformationen in der Fourier-Transformation an“. .”

Das folgende Diagramm zeigt das Spektrum einer AC-gekoppelten Rechteckwelle mit einer Amplitude von 1 und einer Frequenz von 1 Hz.

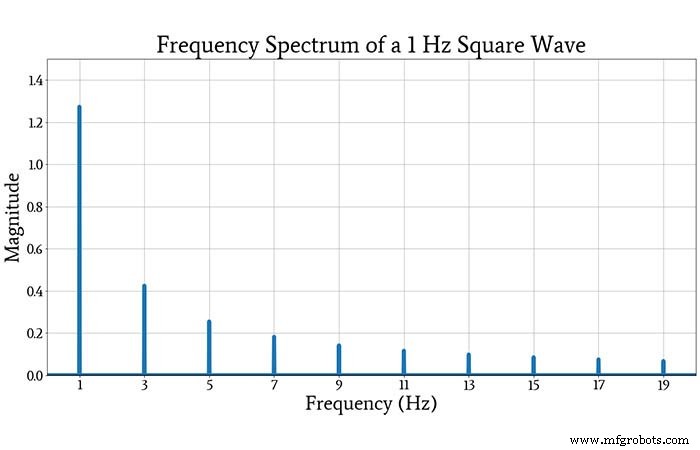
Wenn Sie die aufgetragenen Amplituden der Frequenz-„Spitzen“ mit den Amplituden der entsprechenden Sinuskomponenten in der oben diskutierten unendlichen Reihe vergleichen, werden Sie feststellen, dass sie konsistent sind.

Berechnung der Fourier-Transformation

Wir sind fast am Ende dieses Artikels angelangt, und ich habe Ihnen immer noch nicht gesagt, wie wir die Fourier-Transformation eines mathematisch definierten Signals tatsächlich erzeugen.

Um ehrlich zu sein, sehe ich keine Notwendigkeit, mathematische Details in einem einführenden Artikel gründlich zu untersuchen:Die Frequenzbereichsanalyse wird heutzutage von benutzerfreundlichen, softwarebasierten Techniken dominiert, und Ingenieure verbringen nicht viel Zeit damit, symbolische Zeit umzuwandeln. Domänenausdrücke in symbolische Frequenzdomänenausdrücke.

Nichtsdestotrotz ist es bei etwas so Wichtigem wie der Fourier-Transformation gut, sich zumindest der zugrunde liegenden Mathematik bewusst zu sein. Also wandeln wir ohne weiteres f(t) in F(ω) um:

\[F(\omega) =\int\limits_{ - \infty}^{ + \infty} {f(t){e^{ - j\omega t} }dt}\]

Schlussfolgerung

Ich hoffe, dass dieser Artikel eine klare, intuitive Erklärung liefert, was die Fourier-Transformation ist und wie sie uns zusätzliche Einblicke in die Natur eines Signals gibt.

Die Fourier-Transformation ist nur der Anfang einer umfangreichen Reihe verwandter Themen; Wenn Sie mehr erfahren möchten, sehen Sie sich die unten aufgeführten Artikel an.

Weitere Lektüre

• Eine Einführung in die diskrete Fourier-Transformation
• Eine Einführung in die schnelle Fourier-Transformation
• So führen Sie eine Frequenzbereichsanalyse mit Scilab durch
• Lernen, im Frequenzbereich zu leben
• Lineare Filterung basierend auf der diskreten Fourier-Transformation