Zwei Techniken zur Linearisierung resistiver Sensorbrücken

Die Messung der winzigen Widerstandsänderungen in Widerstandssensoren kann eine gewaltige Aufgabe sein. Hier sind zwei Hardwaremethoden zum Eliminieren von Nichtlinearitätsfehlern bei Brücken.

Der Widerstand eines resistiven Sensors hängt von einer physikalischen Größe wie Temperatur oder Kraft ab. Die prozentuale Widerstandsänderung dieser Geräte ist normalerweise gering. Beispielsweise kann die Gesamtwiderstandsänderung eines Dehnungsmessstreifens über seinen gesamten Betriebsbereich weniger als 1 % betragen.

Das Erkennen dieser kleinen Werte erfordert hochgenaue Messschaltungen. Brückenschaltungen ermöglichen es uns, diese genauen Messungen einfacher durchzuführen. Der Ausgang einer Brückenschaltung kann jedoch eine nichtlineare Beziehung zur gemessenen physikalischen Größe aufweisen, selbst wenn wir einen linearen Sensor verwenden.

In diesen Fällen können wir entweder Software- oder Hardwaretechniken verwenden, um die Nichtlinearitätsfehler der Brücke zu beseitigen. In diesem Artikel werfen wir einen Blick auf zwei verschiedene Techniken zum Linearisieren von Widerstandssensorbrücken.

Brücken-Nichtlinearität von resistiven Sensoren

Betrachten Sie einen resistiven Drucksensor mit der folgenden linearen Reaktion:

\[R_{sensor} =R_0 + Mx\]

wobei R₀ ist der Anfangswiderstand des Sensors bei Nulldruck, x ist der Wert der Messgröße (Druck) und M ist die Steigung der Sensorantwort. Um unsere zukünftigen Gleichungen zu vereinfachen, nehmen wir an, dass der Wert von M gleich dem Wert des Anfangswiderstands des Sensors ist (R₀ ) und daher ist die Sensorantwort \[R_0(1+x)\].

Normalerweise ist die prozentuale Änderung des Widerstands eines Widerstandssensors gering und wir müssen eine Brückenschaltung verwenden, um genaue Messungen einfacher durchführen zu können. Eine gängige Brückenkonfiguration für diesen Sensor ist in Abbildung 1 dargestellt.

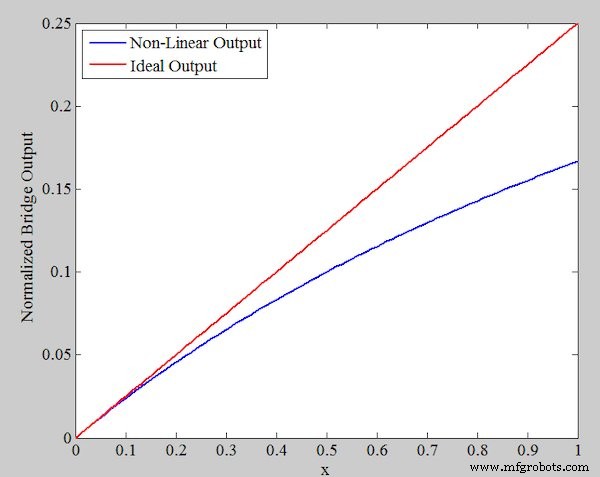
Abbildung 1. Gemeinsame Brückenkonfiguration eines Widerstandssensors

Beachten Sie, dass die anderen drei Widerstände der Brücke einen Widerstandswert von R₀ . haben . Diese Auswahl an Brückenwiderständen maximiert die Empfindlichkeit des Ausgangs (V_out ) auf Änderungen des Sensorwiderstands. Die Ausgangsgleichung kann erhalten werden als:

\[V_{out} =V_A - V_B =V_r\left(\frac{R_0(1+x)}{R_0+R_0(1+x)} - \frac {1}{2}\right)\]

Dies vereinfacht sich zu:

\[V_{out} =V_r\left(\frac{x}{2(2+x)}\right)\]

Gleichung 1.

Wie Sie sehen, ist der Zusammenhang zwischen dem Brückenausgang und der Änderung des Widerstandswerts (x) nicht linear. Mit \[x\ll2\] können wir die obige Gleichung durch die folgende lineare Beziehung approximieren:

\[V_{out} \approx V_r\left(\frac{x}{4}\right)\]

Gleichung 2.

Abbildung 2 zeigt die normalisierte Ausgabe der Brücke \[\frac{V_{out}}{V_r}\] sowohl für den tatsächlichen Fall (Gleichung 1) als auch für die ideale Ausgabe (Gleichung 2).

Abbildung 2. Nichtlineare (blau) und ideale (rot) Ausgaben der Gleichungen 1 und 2

Erwartungsgemäß nimmt die Abweichung von der linearen Antwort mit x zu.

Wie viel Nichtlinearitätsfehler wird eingeführt?

Quantifizieren wir den Nichtlinearitätsfehler der obigen Brückenschaltung. Wir können Gleichung 1 umschreiben als:

\[V_{out} =V_r \left(\frac{x}{4}\right) \left(\frac{1}{1+ \frac{x} {2}}\right)\]

Angenommen, \[\frac{x}{2} <<1\] können wir den Satz von Taylor verwenden, um eine Approximation der obigen Funktion zu erhalten als:

\[V_{out} =V_r\left(\frac{x}{4}\right)\left(1 - \frac{x}{2}\right) \]

Wenn wir dieses Ergebnis mit Gleichung 2 vergleichen, können wir die Größe des Fehlers wie folgt berechnen:

\[E_{Nichtlinearität} =V_r\left(\frac{x}{4}\right)\left(\frac{x}{2}\right) \]

Wenn wir dies durch den erwarteten Idealwert gemäß Gleichung 2 dividieren, können wir den prozentualen Linearitätsfehler des Endpunkts für eine gegebene Widerstandsänderung (x) erhalten:

\[Percentage~Error =\frac{x}{2} \times 100\%\]

Beispiel für die Berechnung des Nichtlinearitätsfehlers

Betrachten Sie einen Sensor mit Antwort \[R_{sensor} =R_0(1+x)\]. Nehmen Sie an, dass \[R_0 =100~\Omega\] und der maximale Wert von x über den gesamten Betriebsbereich 0,01 beträgt. Der maximale Prozentsatz des Linearitätsfehlers beträgt:

\[Percentage~Error =\left(\frac{0.01}{2}\right) \times 100\% =0.5\%\]

Beachten Sie, dass, obwohl wir Software verwenden können, um die Linearitätsfehler des Sensors zu beseitigen, eine lineare Reaktion wünschenswert ist, da dies die Messgenauigkeit erhöht und die Systemkalibrierung erleichtert. Es gibt verschiedene Schaltungstopologien, die verwendet werden können, um Brückenschaltungen zu linearisieren.

Im Rest dieses Artikels werden wir zwei verschiedene Techniken zur Brückenlinearisierung untersuchen.

Methode 1:Erstellen einer Spannung proportional zu Widerstandsänderungen (x)

Die erste Linearisierungstechnik, die wir in diesem Artikel diskutieren, ist in Abbildung 3 dargestellt. Lassen Sie uns zunächst die Grundidee dieser Technik untersuchen und dann sehen, wie die Schaltung in Abbildung 3 diese Idee implementiert.

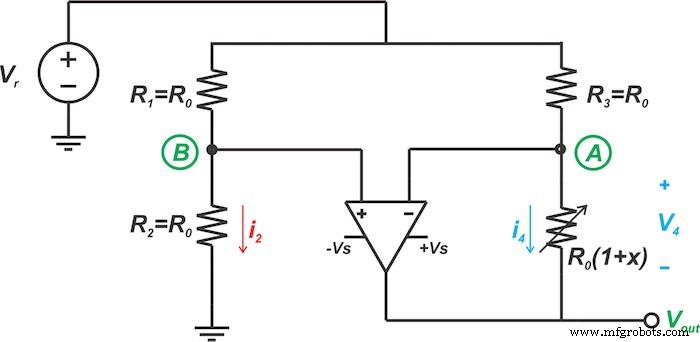
Abbildung 3. Ein Schaltungstyp zum Linearisieren von Widerstandssensorbrücken

Abbildung 4 zeigt eine Darstellung eines festen Stroms von \[I_{Ref}\] gezwungen, durch unseren Linearsensor zu fließen.

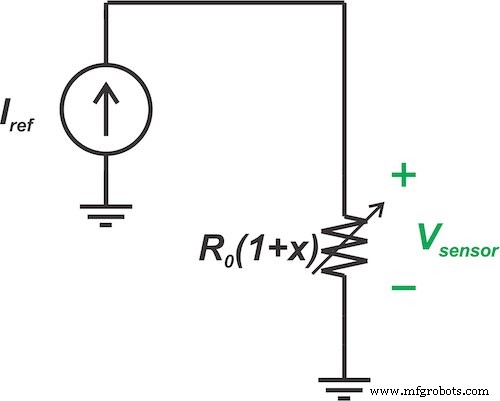
Abbildung 4. Ein fester Strom (I_Ref ) durch einen Linearsensor gezwungen

In diesem Szenario wäre die resultierende Spannung am Sensor:

\[V_{sensor} =I_{Ref} \times R_0(1 + x)\]

das kann neu angeordnet werden als:

\[V_{sensor} =R_0 \times I_{Ref} + R_0 \times I_{Ref} \times x\]

Während der erste Term ein konstanter Wert ist, ist der zweite Term proportional zu den Änderungen des Sensorwiderstands (x). Wenn wir den konstanten Term weglassen können, haben wir eine Spannung, die eine lineare Beziehung zu x hat.

Schaltungsimplementierung

Die Schaltung in Abbildung 3 verwendet die obige Idee, um die Brückenschaltung zu linearisieren. Da die Eingänge des Operationsverstärkers idealerweise keinen Strom ziehen, hat die Spannung am Knoten B einen konstanten Wert von:

\[v_B =\frac{R_0}{R_0 + R_0}V_r =\frac{V_r}{2}\]

Die negative Rückkopplung zusammen mit der hohen Verstärkung des Operationsverstärkers zwingt sowohl die invertierenden als auch die nicht invertierenden Eingänge des Operationsverstärkers dazu, dieselbe Spannung zu haben:

\[v_A =v_B =\frac{V_r}{2}\]

Da beide Enden von R3 auf konstanten Potentialen liegen, fließt ein konstanter Strom durch sie. Mit anderen Worten, der Operationsverstärker lässt R3 als Stromquelle wirken, die einen konstanten Strom von \[\frac{V_r}{2R_0}\] in den Sensor zwingt. Daher beträgt die Spannung am Sensor:

\[V_4 =\frac{V_r}{2R_0} \times R_0(1 + x) =\frac{V_r}{2} + \frac{V_r}{2} x\]

Der erste Term ist der konstante Wert, der aus dem V_out . eliminiert werden soll Gleichung. Der zweite Term ist proportional zu den Sensorwiderstandsänderungen (x) und sollte in der Ausgangsgleichung erscheinen. Unter Anwendung des Kirchhoffschen Spannungsgesetzes finden wir V_out als:

\[V_{out} =-V_4 + V_A =- \left(\frac{V_r}{2} + \frac{V_r}{2}x\right) + V_A\]

Daher brauchen wir nur V_A gleich \[\frac{V_r}{2}\]. Dies ist bereits erfüllt, was zu:

. führt

\[V_{out} =-\frac{V_r}{2}x\]

Daher hat die Ausgabe eine lineare Beziehung zu x.

Methode 2:Erstellen eines Stroms proportional zu den Widerstandsänderungen (x)

Die zweite Brückenlinearisierungstechnik, die wir in diesem Artikel besprechen, ist in Abbildung 5 dargestellt.

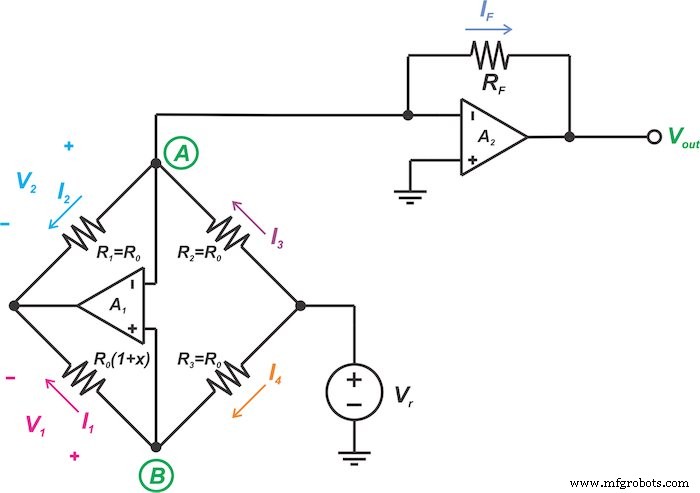
Abbildung 5. Eine weitere Schaltung zur analogen Linearisierung von resistiven Sensorbrücken

Lassen Sie uns noch einmal einen Blick auf die Grundidee dieser Technik werfen und dann ihre Schaltungsimplementierung untersuchen.

Diese zweite Linearisierungstechnik ist in Abbildung 6 dargestellt.

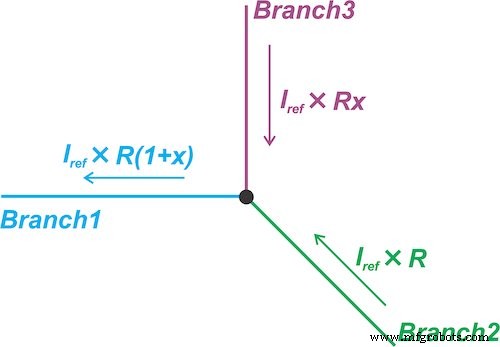
Abbildung 6. Linearisierungstechnik, die den Strom durch einen Zweig des Stromkreises erzwingt, um proportional zum Widerstand des Sensors zu sein

Es zwingt den Strom durch einen Zweig des Stromkreises (Zweig 1) proportional zum Sensorwiderstand zu sein:

\[I_1 =I_{Ref} \times R_0(1 + x)\]

wobei ich_Ref ist ein konstanter Wert. Dann führt es eine Subtraktion des Strombereichs durch, um den konstanten Term \[I_{Ref} \times R_0\] zu eliminieren. Zu diesem Zweck wird der Strom durch Zweig 2 auf \[I_{Ref} \times R_0\] gesetzt. Daher ist der Strom durch Zweig 3 \[I_{Ref} \times R_0x\]— proportional zu den Änderungen des Sensorwiderstands (x).

Schaltungsimplementierung

Sehen wir uns an, wie die Schaltung in Abbildung 5 die obige Idee implementiert. Auch hier erzwingt die negative Rückkopplung zusammen mit der hohen Verstärkung der Operationsverstärker sowohl die invertierenden als auch die nicht invertierenden Eingänge der beiden Operationsverstärker (beide A₁ und A₂ ) um die gleiche Spannung zu haben:

\[v_A =v_B =0\]

Gleichung 3.

Daher haben wir V₁ =V₂ das führt zu

\[R_0 (1 + x) \times I_1 =R_0 \times I_2\]

Dies vereinfacht sich zu:

\[I_2 =I_1 + I_1 \times x\]

Gleichung 4.

Wir wissen, dass I₁ =I₄ und unter Berücksichtigung von Gleichung 3 haben wir:

\[I_1 =I_4 =\frac{V_r - v_A}{R_0} =\frac{V_r}{R_0}\]

Setzen wir dies in Gleichung 4 ein, erhalten wir:

\[I_2 =\frac{V_r}{R_0} + \frac{V_r}{R_0} \times x\]

Daher I₂ ist die Summe aus einem konstanten Wert und einem zu x proportionalen Term. Wir brauchen nur das Kirchhoffsche Stromgesetz zu verwenden, um den konstanten Term in der Ausgangsstromgleichung zu eliminieren. Der Strom durch R2 erzeugt einen Strom gleich \[\frac{V_r}{R_0}\] zu Knoten A, führt zu:

\[I_F =-\frac{V_r}{R_0} \times x\]

Daher erhalten wir:

\[V_{out} =V_r \times \frac{R_F}{R_0} \times x\]

Die Schaltung in Abbildung 5 benötigt im Vergleich zur ersten Technik einen zusätzlichen Operationsverstärker. Bei den beiden Op-Amp-Lösungen können wir die Verstärkung jedoch beliebig einstellen, indem wir das Verhältnis \[\frac{R_F}{R_0}\] wählen.

---

Um eine vollständige Liste meiner Artikel zu sehen, besuchen Sie bitte diese Seite.