Ableitungen von Potenzfunktionen von e

Beispiel für Ableitungen von e

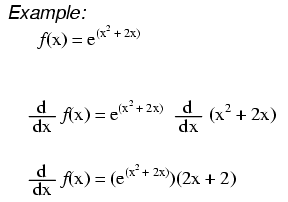
Proportionalitätskonstante

Wenn wir sagen, dass eine Beziehung oder ein Phänomen „exponentiell“ ist, implizieren wir, dass eine Menge – elektrischer Strom, Gewinne, Bevölkerung – mit zunehmender Menge schneller zunimmt. Mit anderen Worten, die Änderungsrate bezüglich einer gegebenen Variablen ist proportional zum Wert dieser Variablen. Dies bedeutet, dass die Ableitung einer Exponentialfunktion gleich der ursprünglichen Exponentialfunktion multipliziert mit einer Konstanten (k ), der die Verhältnismäßigkeit herstellt.

$$\frac{\text{d}}{\text{d}x}a^x=ka^x$$

Die Proportionalitätskonstante ist gleich dem natürlichen Logarithmus der Basis des Exponenten:

$$\frac{\text{d}}{\text{d}x}a^x=\ln(a)\times a^x$$

Daraus folgt, dass, wenn der natürliche Logarithmus der Basis gleich eins ist, die Ableitung der Funktion gleich der ursprünglichen Funktion ist. Genau das passiert mit Potenzfunktionen von e:Der natürliche Logarithmus von e ist 1, und folglich ist die Ableitung von $$e^x$$ $$e^x$$.

$$\frac{\text{d}}{\text{d}x}e^x=e^x$$

Die "Kettenregel"

Wenn der Exponentialausdruck etwas anderes als einfach x ist, wenden wir die Kettenregel an:Zuerst nehmen wir die Ableitung des gesamten Ausdrucks, dann multiplizieren wir sie mit der Ableitung des Ausdrucks im Exponenten.

$$\frac{\text{d}}{\text{d}x}e^{x^2+2x}=e^{x^2+2x}\times\frac{\text{d}}{ \text{d}x}(x^2+2x)=(2x+2)e^{x^2+2x}$$

Diese Technik kann verwendet werden, um die Änderungsrate des Diodenstroms in Bezug auf die Diodenspannung zu ermitteln. Die folgende Gleichung liefert eine ungefähre Beziehung zwischen der Spannung an einer Diode ($$V_D$$) und dem Strom durch eine Diode ($$I_D$$):

$$I_D=I_S\times e^\frac{V_D}{0.026}$$

(Weitere Informationen zur Strom-Spannungs-Gleichung von Dioden finden Sie auf der Seite über Dioden und Gleichrichter. Beachten Sie außerdem, dass $$I_S$$ eine Konstante und keine Variable ist.) Um die Änderungsrate des Stroms in Bezug auf die Spannung zu ermitteln, wir nehmen die Ableitung:

$$\frac{\text{d}I_D}{\text{d}V_D}=\frac{\text{d}}{\text{d}V_D}(I_S\times e^\frac{V_D}{ 0.026})=I_S\times e^\frac{V_D}{0.026}\times\frac{1}{0.026}$$

Somit erzeugt bei einem gegebenen Wert der Diodenspannung $$V_D$$ ein inkrementeller Anstieg der Spannung einen Anstieg des Stroms gleich $$\frac{I_S}{0.026}e^\frac{V_D}{0.026}$$ .

VERWANDTE ARBEITSBLÄTTER:

• Arbeitsblatt Calculus for Electric Circuits