Übergangsreaktion des Kondensators

Da Kondensatoren Energie in Form eines elektrischen Feldes speichern, verhalten sie sich in der Regel wie kleine Sekundärbatterien, die elektrische Energie speichern und abgeben können. Ein vollständig entladener Kondensator hält an seinen Anschlüssen null Volt, und ein geladener Kondensator hält eine konstante Spannung an seinen Anschlüssen, genau wie eine Batterie.

Wenn Kondensatoren in einen Stromkreis mit anderen Spannungsquellen geschaltet werden, absorbieren sie Energie aus diesen Quellen, genauso wie eine Sekundärbatterie aufgeladen wird, wenn sie an einen Generator angeschlossen wird. Ein vollständig entladener Kondensator mit einer Klemmenspannung von Null wirkt anfangs als Kurzschluss, wenn er an eine Spannungsquelle angeschlossen wird, und zieht den maximalen Strom, wenn er beginnt, sich aufzuladen.

Im Laufe der Zeit steigt die Klemmenspannung des Kondensators an, um der angelegten Spannung von der Quelle zu entsprechen, und der Strom durch den Kondensator nimmt entsprechend ab. Sobald der Kondensator die volle Spannung der Quelle erreicht hat, wird er keinen Strom mehr ziehen und sich im Wesentlichen wie ein offener Stromkreis verhalten.

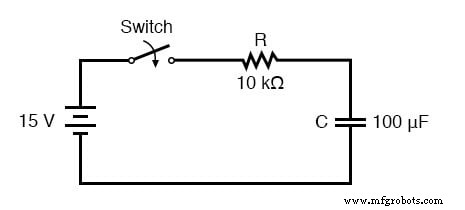
Wenn der Schalter zum ersten Mal geschlossen wird, beträgt die Spannung am Kondensator (von dem uns gesagt wurde, dass er vollständig entladen ist) null Volt; es verhält sich also zunächst wie ein Kurzschluss. Im Laufe der Zeit steigt die Kondensatorspannung auf die gleiche Batteriespannung an und endet in einem Zustand, in dem sich der Kondensator wie ein Leerlauf verhält.

Der Strom durch den Stromkreis wird durch die Spannungsdifferenz zwischen der Batterie und dem Kondensator bestimmt, dividiert durch den Widerstand von 10 kΩ. Wenn sich die Kondensatorspannung der Batteriespannung nähert, nähert sich der Strom Null. Sobald die Kondensatorspannung 15 Volt erreicht hat, ist der Strom genau null. Sehen wir uns an, wie das mit echten Werten funktioniert:

Zeit (Sekunden) Batteriespannung Kondensatorspannung Aktuell 015 V0 V1500 uA0.515 V5.902 V909.8 uA115 V9.482 V551.8 uA215 V12.970 V203.0 uA315 V14.253 V74.68 uA415 V14.725 V27.47 uA515 V14.899 V10.11 uA615 V14. 963 V3.718 µA1015 V14.999 V0.068 µA

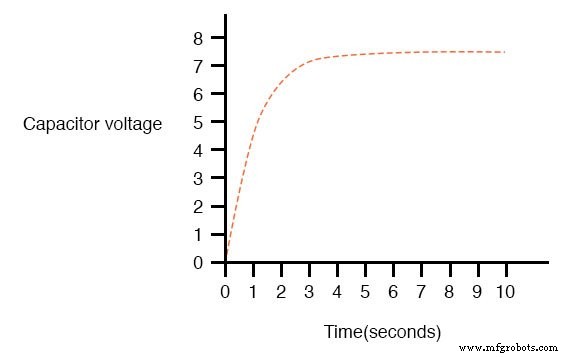
Die Annäherung der Kondensatorspannung an 15 Volt und die Annäherung des Stroms an Null im Laufe der Zeit würde ein Mathematiker als asymptotisch bezeichnen : das heißt, beide nähern sich ihren endgültigen Werten an, kommen sich im Laufe der Zeit immer näher, erreichen aber nie genau ihr Ziel. Für alle praktischen Zwecke können wir jedoch sagen, dass die Kondensatorspannung schließlich 15 Volt erreicht und der Strom schließlich Null wird.

Mit dem SPICE-Schaltungsanalyseprogramm können wir diesen asymptotischen Aufbau der Kondensatorspannung und den Abfall des Kondensatorstroms in einer grafischeren Form darstellen (der Kondensatorstrom wird als Spannungsabfall über dem Widerstand aufgetragen, wobei der Widerstand als Shunt zur Strommessung verwendet wird). :

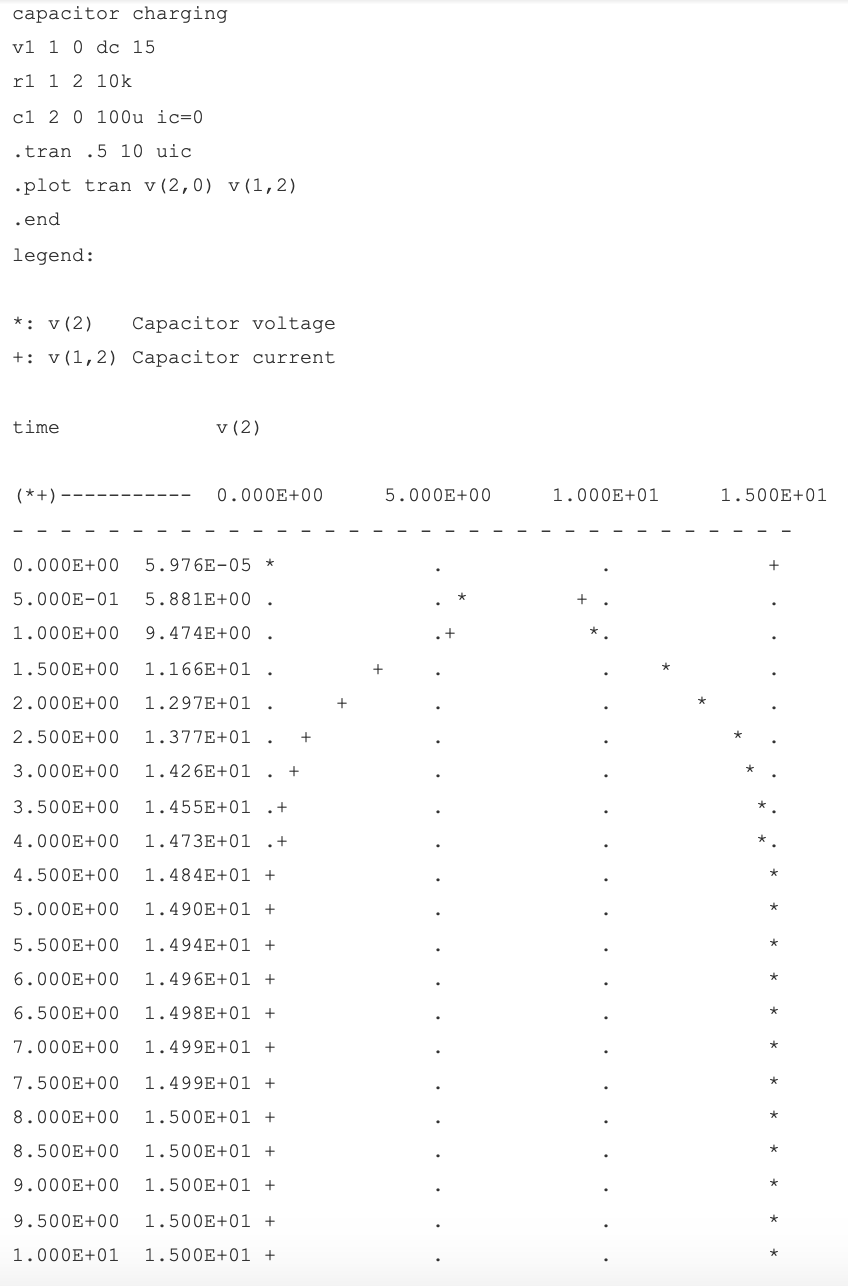
Wie Sie sehen können, habe ich das .plot verwendet Befehl in der Netzliste anstelle des bekannteren .printcommand . Dadurch wird eine pseudografische Darstellung von Figuren auf dem Computerbildschirm unter Verwendung von Textzeichen erzeugt. SPICE zeichnet Graphen so, dass die Zeit auf der vertikalen Achse (nach unten) und die Amplitude (Spannung/Strom) auf der horizontalen (rechts=mehr; links=weniger) aufgetragen ist.

Beachten Sie, wie die Spannung (rechts von der Kurve) zunächst sehr schnell ansteigt und dann im Laufe der Zeit abnimmt. Der Strom ändert sich auch zunächst sehr schnell und flacht dann im Laufe der Zeit ab, nähert sich jedoch dem Minimum (links von der Skala), während sich die Spannung dem Maximum nähert.

RÜCKBLICK:

• Kondensatoren verhalten sich bei einer plötzlichen Änderung der angelegten Spannung ähnlich wie Sekundärbatterien:Sie reagieren zunächst mit einem hohen Strom, der mit der Zeit abnimmt.
• Ein vollständig entladener Kondensator wirkt bei plötzlichem Anlegen von Spannung zunächst wie ein Kurzschluss (Strom ohne Spannungsabfall). Nach dem vollständigen Aufladen auf dieses Spannungsniveau wirkt es als offener Stromkreis (Spannungsabfall ohne Strom).
• In einer Widerstands-Kondensator-Ladeschaltung geht die Kondensatorspannung von Null auf die volle Quellenspannung, während der Strom vom Maximum auf Null steigt. Beide Variablen ändern sich zunächst am schnellsten und nähern sich mit der Zeit immer langsamer ihren Endwerten.

VERWANDTE ARBEITSBLÄTTER:

• Arbeitsblatt für Zeitkonstantenschaltungen
• Arbeitsblatt zur Berechnung von Zeitkonstanten