AC-Kondensatorschaltungen

Kondensatoren vs. Widerstände

Kondensatoren verhalten sich nicht wie Widerstände. Während Widerstände einen direkt proportional zum Spannungsabfall proportionalen Elektronenfluss zulassen, wirken Kondensatoren Änderungen entgegen in Spannung, indem sie beim Laden oder Entladen auf den neuen Spannungspegel Strom ziehen oder liefern.

Der Elektronenfluss „durch“ einen Kondensator ist direkt proportional zur Änderungsrate der Spannung am Kondensator. Dieser Widerstand gegen Spannungsänderungen ist eine andere Form der Reaktanz , aber genau das Gegenteil von Induktoren.

Eigenschaften der Kondensatorschaltung

Mathematisch ausgedrückt ist die Beziehung zwischen dem Strom „durch“ den Kondensator und der Spannungsänderungsrate am Kondensator wie folgt:

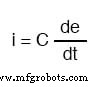
Der Ausdruck de/dt ist eine aus der Infinitesimalrechnung, was die Änderungsrate der Momentanspannung (e) über die Zeit in Volt pro Sekunde bedeutet. Die Kapazität (C) ist in Farad angegeben und der Momentanstrom (i) natürlich in Ampere.

Manchmal finden Sie die Geschwindigkeit der momentanen Spannungsänderung über die Zeit als dv/dt anstelle von de/dt:Verwenden Sie stattdessen den Kleinbuchstaben „v“ oder „e“, um die Spannung darzustellen, aber es bedeutet genau dasselbe. Um zu zeigen, was mit Wechselstrom passiert, analysieren wir eine einfache Kondensatorschaltung:

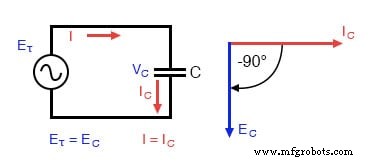
Reine kapazitive Schaltung:Kondensatorspannung eilt dem Kondensatorstrom um 90° nach

Wenn wir Strom und Spannung für diese sehr einfache Schaltung aufzeichnen würden, würde sie ungefähr so ​​aussehen:

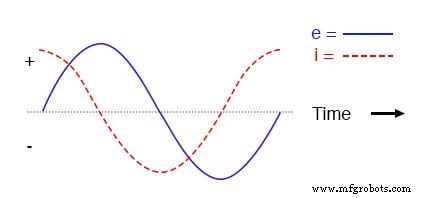
Reine kapazitive Schaltungswellenformen.

Denken Sie daran, der Strom durch einen Kondensator ist eine Reaktion auf die Änderung in Spannung darüber.

Daher ist der Momentanstrom null, wenn die Momentanspannung einen Spitzenwert aufweist (Nulländerung oder Pegelsteigung auf der Spannungssinuswelle), und der Momentanstrom hat überall dort einen Spitzenwert, wo die Momentanspannung eine maximale Änderung aufweist (die Punkte von steilste Steigung der Spannungswelle, wo sie die Nulllinie kreuzt).

Dies führt zu einer Spannungswelle, die zur Stromwelle um -90° phasenverschoben ist. Betrachtet man das Diagramm, scheint die Stromwelle einen „Vorsprung“ gegenüber der Spannungswelle zu haben; der Strom „eilt“ der Spannung voraus und die Spannung „hinkt“ dem Strom hinterher.

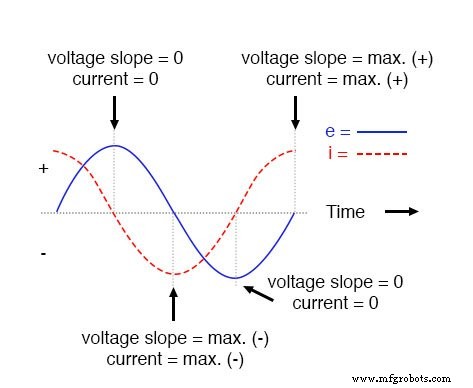
Spannung eilt dem Strom in einer rein kapazitiven Schaltung um 90° nach.

Wie Sie vielleicht erraten haben, ist die gleiche ungewöhnliche Leistungswelle, die wir bei der einfachen Induktorschaltung gesehen haben, auch in der einfachen Kondensatorschaltung vorhanden:

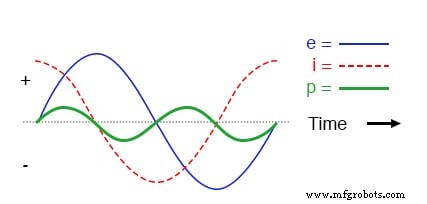
In einer rein kapazitiven Schaltung kann die Momentanleistung positiv oder negativ sein.

Wie bei der einfachen Induktorschaltung führt die 90-Grad-Phasenverschiebung zwischen Spannung und Strom zu einer Leistungswelle, die gleichermaßen zwischen positiv und negativ wechselt. Dies bedeutet, dass ein Kondensator keine Leistung verbraucht, da er auf Spannungsänderungen reagiert; es absorbiert und gibt nur abwechselnd Energie ab.

Reaktanz eines Kondensators

Der Widerstand eines Kondensators gegen Spannungsänderungen bedeutet im Allgemeinen einen Widerstand gegen Wechselspannung, der sich definitionsgemäß immer in augenblicklicher Größe und Richtung ändert.

Für jede gegebene Wechselspannung bei einer gegebenen Frequenz „leitet“ ein Kondensator einer gegebenen Größe einen bestimmten Wechselstrom.

So wie der Strom durch einen Widerstand eine Funktion der Spannung am Widerstand und des vom Widerstand gebotenen Widerstands ist, ist der Wechselstrom durch einen Kondensator eine Funktion der Wechselspannung an ihm und der Reaktanz bietet der Kondensator.

Wie bei Induktivitäten wird die Reaktanz eines Kondensators in Ohm ausgedrückt und durch den Buchstaben X (oder genauer gesagt XC) symbolisiert.

Da Kondensatoren Strom proportional zur Spannungsänderungsrate „leiten“, leiten sie mehr Strom für sich schneller ändernde Spannungen (da sie sich in kürzerer Zeit auf die gleichen Spannungsspitzen laden und entladen) und weniger Strom für sich langsamer ändernde Spannungen.

Dies bedeutet, dass die Reaktanz in Ohm für jeden Kondensator invers ist proportional zur Frequenz des Wechselstroms.

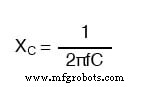
Reaktanz eines 100-uF-Kondensators:

Frequenz (Hertz) Reaktanz (Ohm) 6026.525812013.262925000.6366

Bitte beachten Sie, dass das Verhältnis der kapazitiven Reaktanz zur Frequenz dem der induktiven Reaktanz genau entgegengesetzt ist.

Die kapazitive Reaktanz (in Ohm) nimmt mit steigender Wechselstromfrequenz ab. Umgekehrt nimmt die induktive Reaktanz (in Ohm) mit steigender Wechselstromfrequenz zu. Induktoren wirken sich schneller ändernden Strömen entgegen, indem sie größere Spannungsabfälle erzeugen; Kondensatoren wirken schnelleren Spannungsabfällen entgegen, indem sie größere Ströme zulassen.

Wie bei Induktoren kann der 2πf-Term der Reaktanzgleichung durch den griechischen Kleinbuchstaben Omega (ω) ersetzt werden, der als Winkelgeschwindigkeit . bezeichnet wird des Wechselstromkreises. Somit könnte die Gleichung XC =1/(2πfC) auch als XC =1/(ωC) geschrieben werden, wobei ω in Einheiten von Radiant pro Sekundeω ausgedrückt wird .

Wechselstrom in einer einfachen kapazitiven Schaltung ist gleich der Spannung (in Volt) geteilt durch die kapazitive Reaktanz (in Ohm), genauso wie Wechsel- oder Gleichstrom in einer einfachen Widerstandsschaltung gleich der Spannung (in Volt) geteilt durch die Widerstand (in Ohm). Die folgende Schaltung veranschaulicht diesen mathematischen Zusammenhang am Beispiel:

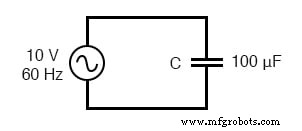
Kapazitive Reaktanz.

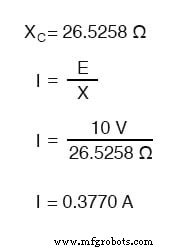
Wir müssen jedoch bedenken, dass Spannung und Strom hier nicht in Phase sind. Wie bereits gezeigt, weist der Strom eine Phasenverschiebung von +90° gegenüber der Spannung auf. Wenn wir diese Phasenwinkel von Spannung und Strom mathematisch darstellen, können wir den Phasenwinkel des reaktiven Widerstands des Kondensators zum Strom berechnen.

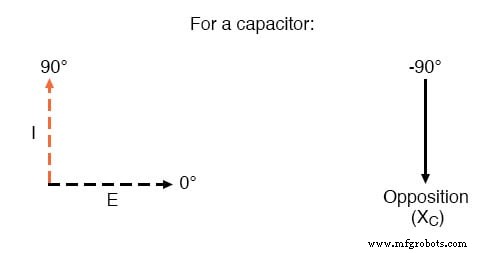
Spannung eilt dem Strom in einem Kondensator um 90° nach.

Mathematisch sagen wir, dass der Phasenwinkel des Widerstands eines Kondensators zum Strom -90° beträgt, was bedeutet, dass der Widerstand eines Kondensators zum Strom eine negative imaginäre Größe ist. (Siehe Abbildung oben.) Dieser Phasenwinkel des reaktiven Widerstands zum Strom wird bei der Schaltungsanalyse von entscheidender Bedeutung, insbesondere bei komplexen Wechselstromkreisen, bei denen Reaktanz und Widerstand interagieren.

Es wird sich als vorteilhaft erweisen, jede zu vertreten Widerstand der Komponente zum Strom in Form komplexer Zahlen und nicht nur skalarer Größen von Widerstand und Reaktanz.

RÜCKBLICK:

• Kapazitive Reaktanz ist der Gegensatz, den ein Kondensator dem Wechselstrom aufgrund seiner phasenverschobenen Speicherung und Abgabe von Energie in seinem elektrischen Feld bietet. Die Reaktanz wird durch den Großbuchstaben „X“ symbolisiert und wird ebenso wie der Widerstand (R) in Ohm gemessen.
• Die kapazitive Reaktanz kann mit dieser Formel berechnet werden:XC =1/(2πfC)
• Kapazitive Reaktanz abnimmt mit zunehmender Frequenz. Mit anderen Worten, je höher die Frequenz, desto weniger widersetzt sie sich (je mehr „leitet“) sie dem Wechselstrom.

VERWANDTE ARBEITSBLÄTTER:

• Arbeitsblatt Kondensatoren