SciPy in Python Tutorial:Was ist | Beispiele für Bibliotheken und Funktionen
SciPy in Python
SciPy in Python ist eine Open-Source-Bibliothek zur Lösung mathematischer, wissenschaftlicher, ingenieurwissenschaftlicher und technischer Probleme. Es ermöglicht Benutzern, die Daten zu manipulieren und die Daten mit einer Vielzahl von High-Level-Python-Befehlen zu visualisieren. SciPy basiert auf der Python NumPy-Erweiterung. SciPy wird auch als „Sigh Pi“ ausgesprochen.
Unterpakete von SciPy:
- Dateieingabe/-ausgabe – scipy.io
- Sonderfunktion – scipy.special
- Operation der linearen Algebra – scipy.linalg
- Interpolation – scipy.interpolate
- Optimierung und Passform – scipy.optimize
- Statistiken und Zufallszahlen – scipy.stats
- Numerische Integration – scipy.integrate
- Schnelle Fourier-Transformationen – scipy.fftpack
- Signalverarbeitung – scipy.signal
- Bildbearbeitung – scipy.ndimage
In diesem Python-SciPy-Tutorial lernen Sie:
- Was ist SciPy?
- Warum SciPy verwenden?
- Numpy VS SciPy
- SciPy – Installation und Einrichtung der Umgebung
- Datei-Eingabe-/Ausgabepaket:
- Spezialfunktionspaket:
- Lineare Algebra mit SciPy:
- Diskrete Fourier-Transformation – scipy.fftpack
- Optimierung und Anpassung in SciPy – scipy.optimize
- Nelder-Mead-Algorithmus:
- Bildverarbeitung mit SciPy – scipy.ndimage
Warum SciPy verwenden
- SciPy enthält verschiedene Unterpakete, die helfen, die häufigsten Probleme im Zusammenhang mit wissenschaftlicher Berechnung zu lösen.
- Das SciPy-Paket in Python ist die am häufigsten verwendete wissenschaftliche Bibliothek, nur an zweiter Stelle nach der GNU Scientific Library für C/C++ oder Matlab.
- Einfach zu bedienen und zu verstehen sowie schnelle Rechenleistung.
- Es kann mit einem Array von NumPy-Bibliotheken arbeiten.
Numpy VS SciPy
Numpy:
- Numpy ist in C geschrieben und wird für mathematische oder numerische Berechnungen verwendet.
- Es ist schneller als andere Python-Bibliotheken
- Numpy ist die nützlichste Bibliothek für Data Science, um grundlegende Berechnungen durchzuführen.
- Numpy enthält nichts als Array-Datentypen, die die grundlegendsten Operationen wie Sortieren, Formen, Indizieren usw. ausführen.
SciPy:
- SciPy ist in NumPy integriert
- Das SciPy-Modul in Python ist eine voll funktionsfähige Version der linearen Algebra, während Numpy nur wenige Funktionen enthält.
- Die meisten neuen Data-Science-Funktionen sind in Scipy statt in Numpy verfügbar.
SciPy – Installation und Einrichtung der Umgebung
Sie können SciPy auch unter Windows über pip
installierenPython3 -m pip install --user numpy scipy
Installieren Sie Scipy unter Linux
sudo apt-get install python-scipy python-numpy
Installieren Sie SciPy auf dem Mac
sudo port install py35-scipy py35-numpy
Bevor wir mit dem Erlernen von SciPy Python beginnen, müssen Sie grundlegende Funktionen sowie verschiedene Arten eines Arrays von NumPy
kennenDie Standardmethode zum Importieren von SciPy-Modulen und Numpy:
from scipy import special #same for other modules import numpy as np
Datei-Eingabe-/Ausgabepaket:
Scipy, I/O-Paket, hat eine breite Palette von Funktionen für die Arbeit mit verschiedenen Dateiformaten, darunter Matlab, Arff, Wave, Matrix Market, IDL, NetCDF, TXT, CSV und Binärformat.
Nehmen wir ein Beispiel für ein Dateiformat Python SciPy, wie es regelmäßig in MatLab verwendet wird:
import numpy as np
from scipy import io as sio
array = np.ones((4, 4))
sio.savemat('example.mat', {'ar': array})
data = sio.loadmat(‘example.mat', struct_as_record=True)
data['ar']
Ausgabe:
array([[ 1., 1., 1., 1.],
[ 1., 1., 1., 1.],
[ 1., 1., 1., 1.],
[ 1., 1., 1., 1.]])
Code-Erklärung
- Zeile 1 &2: Importieren Sie die wesentliche SciPy-Bibliothek in Python mit I/O-Paket und Numpy.
- Zeile 3 :Erstellen Sie ein 4 x 4, dimensionales Einsen-Array
- Zeile 4 :Array in example.mat speichern Datei.
- Zeile 5: Holen Sie sich Daten von example.mat Datei
- Zeile 6 :Ausgabe drucken.
Spezialfunktionspaket
- scipy.special Paket enthält zahlreiche Funktionen der mathematischen Physik.
- Die SciPy-Sonderfunktion umfasst Kubikwurzel, Exponential, Log-Summe Exponential, Lambert, Permutation und Kombinationen, Gamma, Bessel, Hypergeometrie, Kelvin, Beta, parabolischer Zylinder, Exponential mit relativem Fehler usw.
- Für eine einzeilige Beschreibung all dieser Funktionen geben Sie in der Python-Konsole ein:
help(scipy.special)
Output :
NAME
scipy.special
DESCRIPTION
========================================
Special functions (:mod:`scipy.special`)
========================================
.. module:: scipy.special
Nearly all of the functions below are universal functions and follow
broadcasting and automatic array-looping rules. Exceptions are noted.
Kubikwurzelfunktion:
Die Kubikwurzelfunktion findet die Kubikwurzel von Werten.
Syntax:
scipy.special.cbrt(x)
Beispiel:
from scipy.special import cbrt #Find cubic root of 27 & 64 using cbrt() function cb = cbrt([27, 64]) #print value of cb print(cb)
Ausgabe: array([3., 4.])
Exponentialfunktion:
Die Exponentialfunktion berechnet die 10**x elementweise.
Beispiel:
from scipy.special import exp10 #define exp10 function and pass value in its exp = exp10([1,10]) print(exp)
Ausgabe:[1.e+01 1.e+10]
Permutationen &Kombinationen:
SciPy bietet auch Funktionen zum Berechnen von Permutationen und Kombinationen.
Kombinationen – scipy.special.comb(N,k)
Beispiel:
from scipy.special import comb #find combinations of 5, 2 values using comb(N, k) com = comb(5, 2, exact = False, repetition=True) print(com)
Ausgabe:15,0
Permutationen –
scipy.special.perm(N,k)
Beispiel:
from scipy.special import perm #find permutation of 5, 2 using perm (N, k) function per = perm(5, 2, exact = True) print(per)
Ausgabe:20
Logsummen-Exponentialfunktion
Log Sum Exponential berechnet den Log des Summen-Exponential-Eingabeelements.
Syntax:
scipy.special.logsumexp(x)
Bessel-Funktion
Berechnungsfunktion der n-ten ganzzahligen Ordnung
Syntax:
scipy.special.jn()
Lineare Algebra mit SciPy
- Lineare Algebra von SciPy ist eine Implementierung von BLAS- und ATLAS LAPACK-Bibliotheken.
- Die Leistung von Linear Algebra ist im Vergleich zu BLAS und LAPACK sehr schnell.
- Lineare Algebra-Routine akzeptiert zweidimensionale Array-Objekte und die Ausgabe ist auch ein zweidimensionales Array.
Lassen Sie uns nun einen Test mit scipy.linalg durchführen
Determinante berechnen einer zweidimensionalen Matrix,
from scipy import linalg import numpy as np #define square matrix two_d_array = np.array([ [4,5], [3,2] ]) #pass values to det() function linalg.det( two_d_array )
Ausgabe: -7,0
Inverse Matrix –
scipy.linalg.inv()
Inverse Matrix of Scipy berechnet die Inverse jeder quadratischen Matrix.
Mal sehen,
from scipy import linalg import numpy as np # define square matrix two_d_array = np.array([ [4,5], [3,2] ]) #pass value to function inv() linalg.inv( two_d_array )
Ausgabe:
array( [[-0.28571429, 0.71428571],
[ 0.42857143, -0.57142857]] )
Eigenwerte und Eigenvektor
scipy.linalg.eig()
- Das häufigste Problem in der linearen Algebra sind Eigenwerte und Eigenvektoren, die einfach mit eig() gelöst werden können Funktion.
- Lassen Sie uns nun den Eigenwert von (X finden ) und entsprechen dem Eigenvektor einer zweidimensionalen quadratischen Matrix.
Beispiel
from scipy import linalg import numpy as np #define two dimensional array arr = np.array([[5,4],[6,3]]) #pass value into function eg_val, eg_vect = linalg.eig(arr) #get eigenvalues print(eg_val) #get eigenvectors print(eg_vect)
Ausgabe:
[ 9.+0.j -1.+0.j] #eigenvalues [ [ 0.70710678 -0.5547002 ] #eigenvectors [ 0.70710678 0.83205029] ]
Diskrete Fourier-Transformation – scipy.fftpack
- DFT ist eine mathematische Technik, die bei der Umwandlung räumlicher Daten in Frequenzdaten verwendet wird.
- FFT (Fast Fourier Transformation) ist ein Algorithmus zur Berechnung von DFT
- FFT wird auf ein mehrdimensionales Array angewendet.
- Frequenz definiert die Anzahl von Signalen oder Wellenlängen in einem bestimmten Zeitraum.
Beispiel: Nehmen Sie eine Welle und zeigen Sie mit der Matplotlib-Bibliothek. Wir nehmen das Beispiel einer einfachen periodischen Funktion von sin(20 × 2πt)
%matplotlib inline
from matplotlib import pyplot as plt
import numpy as np
#Frequency in terms of Hertz
fre = 5
#Sample rate
fre_samp = 50
t = np.linspace(0, 2, 2 * fre_samp, endpoint = False )
a = np.sin(fre * 2 * np.pi * t)
figure, axis = plt.subplots()
axis.plot(t, a)
axis.set_xlabel ('Time (s)')
axis.set_ylabel ('Signal amplitude')
plt.show()
Ausgabe:
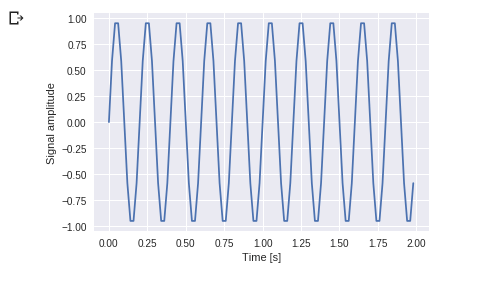
Sie können dies sehen. Die Frequenz beträgt 5 Hz und sein Signal wiederholt sich in 1/5 Sekunden – es ist ein Anruf in einem bestimmten Zeitraum.
Lassen Sie uns nun diese Sinuswelle mit Hilfe der DFT-Anwendung verwenden.
from scipy import fftpack
A = fftpack.fft(a)
frequency = fftpack.fftfreq(len(a)) * fre_samp
figure, axis = plt.subplots()
axis.stem(frequency, np.abs(A))
axis.set_xlabel('Frequency in Hz')
axis.set_ylabel('Frequency Spectrum Magnitude')
axis.set_xlim(-fre_samp / 2, fre_samp/ 2)
axis.set_ylim(-5, 110)
plt.show()
Ausgabe:
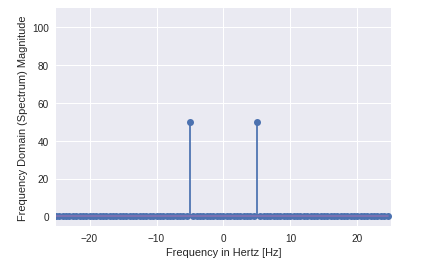
- Sie können deutlich sehen, dass die Ausgabe ein eindimensionales Array ist.
- Eingabe mit komplexen Werten ist Null außer zwei Punkten.
- Im DFT-Beispiel visualisieren wir die Größe des Signals.
Optimierung und Anpassung in SciPy – scipy.optimize
- Die Optimierung bietet einen nützlichen Algorithmus zur Minimierung der Kurvenanpassung, multidimensional oder Skalar- und Wurzelanpassung.
- Nehmen wir ein Beispiel für eine Skalarfunktion um die minimale Skalarfunktion zu finden.
%matplotlib inline
import matplotlib.pyplot as plt
from scipy import optimize
import numpy as np
def function(a):
return a*2 + 20 * np.sin(a)
plt.plot(a, function(a))
plt.show()
#use BFGS algorithm for optimization
optimize.fmin_bfgs(function, 0)
Ausgabe:
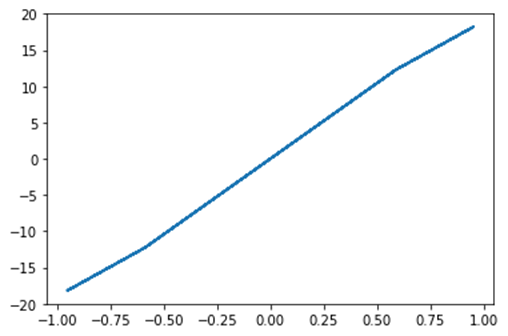
Optimierung erfolgreich beendet.
Aktueller Funktionswert:-23.241676
Iterationen:4
Funktionsauswertungen:18
Gradientenauswertungen:6
Array([-1.67096375])
- In diesem Beispiel erfolgt die Optimierung mit Hilfe des Gradientenabstiegsalgorithmus vom Anfangspunkt
- Aber das mögliche Problem sind lokale Minima statt globaler Minima. Wenn wir keinen Nachbarn von globalen Minima finden, müssen wir eine globale Optimierung anwenden und eine globale Minima-Funktion finden, die als basinhopping() verwendet wird die lokale Optimierer kombiniert.
optimize.basinhopping(function, 0)
Ausgabe:
fun: -23.241676238045315
lowest_optimization_result:
fun: -23.241676238045315
hess_inv: array([[0.05023331]])
jac: array([4.76837158e-07])
message: 'Optimization terminated successfully.'
nfev: 15
nit: 3
njev: 5
status: 0
success: True
x: array([-1.67096375])
message: ['requested number of basinhopping iterations completed successfully']
minimization_failures: 0
nfev: 1530
nit: 100
njev: 510
x: array([-1.67096375])
Nelder-Mead-Algorithmus:
- Nelder-Mead-Algorithmus wählt durch Methodenparameter aus.
- Es bietet die einfachste Art der Minimierung für eine faire Funktion.
- Nelder – Mead-Algorithmus wird nicht für Gradientenauswertungen verwendet, da es länger dauern kann, die Lösung zu finden.
import numpy as np
from scipy.optimize import minimize
#define function f(x)
def f(x):
return .4*(1 - x[0])**2
optimize.minimize(f, [2, -1], method="Nelder-Mead")
Ausgabe:
final_simplex: (array([[ 1. , -1.27109375],
[ 1. , -1.27118835],
[ 1. , -1.27113762]]), array([0., 0., 0.]))
fun: 0.0
message: 'Optimization terminated successfully.'
nfev: 147
nit: 69
status: 0
success: True
x: array([ 1. , -1.27109375])
Bildverarbeitung mit SciPy – scipy.ndimage
- scipy.ndimage ist ein Untermodul von SciPy, das hauptsächlich zum Ausführen einer bildbezogenen Operation verwendet wird
- ndimage bedeutet das „n“-dimensionale Bild.
- SciPy Image Processing bietet Geometrietransformation (Drehen, Zuschneiden, Spiegeln), Bildfilterung (Scharfzeichnen und Entschärfen), Bildanzeige, Bildsegmentierung, Klassifizierung und Extrahierung von Merkmalen.
- MISC-Paket in SciPy enthält vorgefertigte Bilder, die zur Durchführung von Bildbearbeitungsaufgaben verwendet werden können
Beispiel: Nehmen wir ein Beispiel für eine geometrische Transformation von Bildern
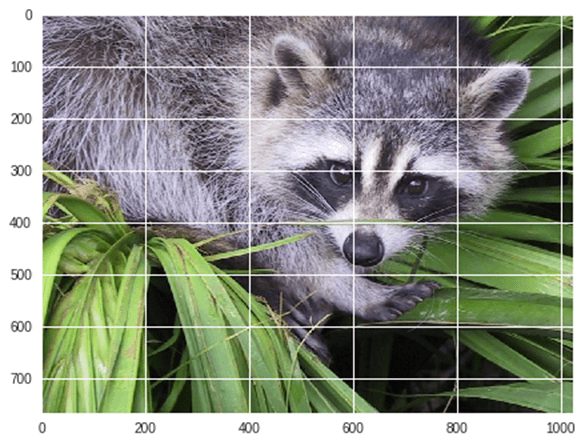
from scipy import misc from matplotlib import pyplot as plt import numpy as np #get face image of panda from misc package panda = misc.face() #plot or show image of face plt.imshow( panda ) plt.show()
Ausgabe:
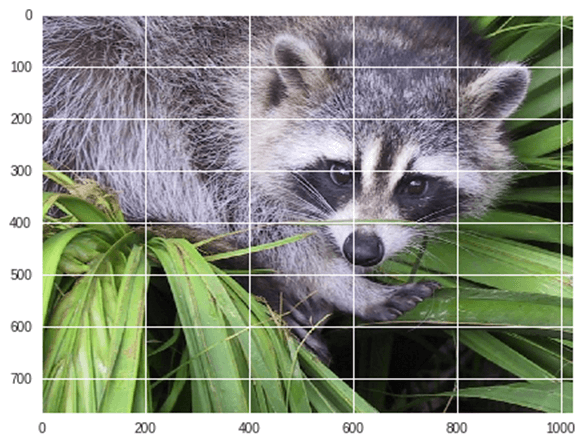
Jetzt klappen wir herunter aktuelles Bild:
#Flip Down using scipy misc.face image flip_down = np.flipud(misc.face()) plt.imshow(flip_down) plt.show()
Ausgabe:
Beispiel: Drehung des Bildes mit Scipy,
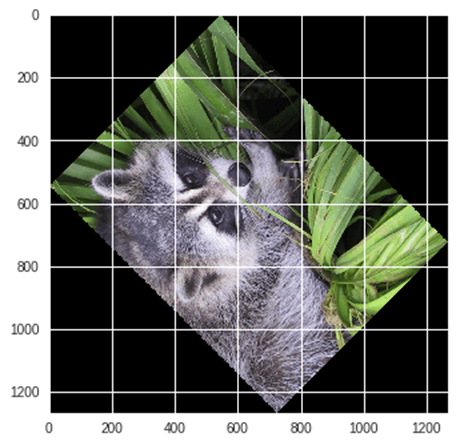
from scipy import ndimage, misc from matplotlib import pyplot as plt panda = misc.face() #rotatation function of scipy for image – image rotated 135 degree panda_rotate = ndimage.rotate(panda, 135) plt.imshow(panda_rotate) plt.show()
Ausgabe:
Integration mit Scipy – Numerische Integration
- Wenn wir eine Funktion integrieren, bei der eine analytische Integration nicht möglich ist, müssen wir uns der numerischen Integration zuwenden
- SciPy bietet Funktionen zur Integration von Funktionen mit numerischer Integration.
- scipy.integrate Die Bibliothek verfügt über einfache Integration, doppelte, dreifache, mehrfache, Gaußsche Quadrat-, Romberg-, Trapez- und Simpson-Regeln.
Beispiel: Nehmen Sie nun ein Beispiel für Single Integration
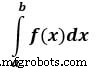
Hier ein ist die Obergrenze und b ist die Untergrenze
from scipy import integrate # take f(x) function as f f = lambda x : x**2 #single integration with a = 0 & b = 1 integration = integrate.quad(f, 0 , 1) print(integration)
Ausgabe:
(0.33333333333333337, 3.700743415417189e-15)
Hier gibt die Funktion zwei Werte zurück, wobei der erste Wert die Integration und der zweite Wert der geschätzte Fehler im Integral ist.
Beispiel:Nehmen Sie nun ein SciPy-Beispiel für doppelte Integration. Wir finden die doppelte Integration der folgenden Gleichung,
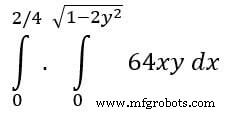
from scipy import integrate import numpy as np #import square root function from math lib from math import sqrt # set fuction f(x) f = lambda x, y : 64 *x*y # lower limit of second integral p = lambda x : 0 # upper limit of first integral q = lambda y : sqrt(1 - 2*y**2) # perform double integration integration = integrate.dblquad(f , 0 , 2/4, p, q) print(integration)
Ausgabe:
(3.0, 9.657432734515774e-14)
Sie haben die obige Ausgabe als dieselbe vorherige gesehen.
Zusammenfassung
- SciPy (ausgesprochen als „Sigh Pi“) ist eine Python-basierte Open-Source-Bibliothek, die in Mathematik, wissenschaftlichem Rechnen, Ingenieurwesen und technischem Rechnen verwendet wird.
- SciPy enthält verschiedene Unterpakete, die helfen, die häufigsten Probleme im Zusammenhang mit wissenschaftlicher Berechnung zu lösen.
- SciPy ist in NumPy integriert
| Paketname | Beschreibung |
|---|---|
| scipy.io |
|
| scipy.special |
|
| scipy.linalg |
|
| scipy.interpolate |
|
| scipy.optimize |
|
| scipy.stats |
|
| scipy.integrate |
|
| scipy.fftpack |
|
| scipy.signal |
|
| scipy.ndimage |
|
Python
- Python Print()-Anweisung:Drucken mit Beispielen
- Python String count() mit BEISPIELE
- Python String format() Erklären Sie mit BEISPIELE
- Python-Lambda-Funktionen mit BEISPIELE
- Python abs() Funktion:Beispiele für absolute Werte
- Python-Funktion round() mit BEISPIELE
- Python map() Funktion mit BEISPIELE
- Python Timeit() mit Beispielen
- Yield in Python Tutorial:Generator &Yield vs. Return Beispiel
- type() und isinstance() in Python mit Beispielen



