Eigenschaften der geometrischen Phase in elektromechanischen Schwingungen von Nanodraht-Resonatoren auf Kohlenstoff-Nanoröhren-Basis

Zusammenfassung

Die geometrische Phase ist eine zusätzliche Phasenentwicklung in der Wellenfunktion von Schwingungen, die potenziell in einem breiten Bereich von Wissenschaft und Technologie anwendbar ist. Die Eigenschaften der geometrischen Phase im gequetschten Zustand für einen Nanodraht-Resonator auf Kohlenstoff-Nanoröhren-Basis wurden mit der Methode des invarianten Operators untersucht. Die Einführung eines linearen invarianten Operators, der für die Behandlung eines komplizierten zeitabhängigen Hamilton-Systems nützlich ist, ermöglichte es uns, die analytische Formel der geometrischen Phase abzuleiten. Ausgehend davon haben wir das zeitliche Verhalten der geometrischen Phase anhand entsprechender Abbildungen analysiert. Der Einfluss von Quetschparametern auf die Entwicklung der geometrischen Phase wurde untersucht. Die geometrische Phase schwingt im großen und ganzen, und die Einhüllende einer solchen Schwingung nimmt mit der Zeit zu. Die Anstiegsrate der geometrischen Phase ist groß, wenn die Parameter wie die klassische Amplitude der Schwingung, der Dämpfungsfaktor und die Amplitude der Antriebskraft groß sind. Wir haben einen sehr starken Anstieg der geometrischen Phase über die Zeit für den Fall bestätigt, dass die Kreisfrequenz des Systems nahe der Resonanzkreisfrequenz liegt. Unsere Entwicklung bezüglich der Eigenschaften der geometrischen Phase ist entscheidend für das Verständnis der topologischen Eigenschaften von Nanodraht-Oszillationen.

Einführung

Mechanische Schwingungen kleinster Resonatoren, wie Kohlenstoff-Nanoröhren-basierte (CNT-basierte) Nanodrähte [1–3], halbleitende Nanodrähte [4], Graphene [5] und schwebende Partikel [6], waren ein Hauptforschungsgegenstand in der Nanowissenschafts-Community seit über einem Jahrzehnt. Aktive Forschungen zu elektromechanischen Schwingungen von Nanodraht-Resonatoren, die durch eine externe periodische Kraft angetrieben werden, wurden sowohl im theoretischen als auch im experimentellen Bereich durchgeführt. Insbesondere CNT-basierte Nanodraht-Resonatoren haben aufgrund ihrer außergewöhnlichen Empfindlichkeit mit hohen Qualitätsfaktoren gegenüber einer kleinen Störung aus der Umgebung großes Interesse als nanoskalige mechanische Vorrichtungen auf sich gezogen. Aufgehängte CNT-basierte Nanodraht-Resonatoren sind vielversprechende Kandidaten für Geräte, die eine Vielzahl physikalischer Größen messen, wie EM-Wellen [2], kleine Kräfte [7], Massen [8], Temperaturen [9] und Geräusche [10].

Analysen der Quantenphasenentwicklung in Nanodraht-Oszillationen sind erforderlich, um die zugrunde liegenden Eigenschaften des Systems theoretisch aufzuklären. Bei den Quantenschwingungszuständen der CNT-basierten Nanodraht-Resonatoren [11] tritt die geometrische Phase [12] sowie die übliche dynamische Phase als ergänzende Weiterentwicklung der Phase auf. Die geometrische Phase [12] ist eine Anholonomik eines Quantenzustands, die in verschiedenen Bereichen der Physik anwendbar ist. Analysen der geometrischen Phase können potenziell zur Charakterisierung von Nanoeigenschaften von Nanodrähten herangezogen werden, wie zum Beispiel Resonanzprofile [13, 14], starke Quantenschwingungen [15, 16], Spannungsrelaxationsmechanismen [17, 18], die Entstehung von Dirac-Magnetoplasmonen [19] und die Topologie der Aharonov-Bohm-Oszillationen [20].

Die Untersuchung der geometrischen Phase in Verbindung mit nichtadiabatischer Dynamik kann einen Einblick in nanomechanische Systeme liefern, der für die Weiterentwicklung genauer Simulationstechniken notwendig ist [21]. Die Vorbereitung, Manipulation und Detektion von Quantenzuständen sind wichtige Faktoren in Quantentechnologien. Ziel der vorliegenden Forschung ist es, das zeitliche Verhalten der geometrischen Phase in Quantenzuständen von Nanodrahtschwingungen aufzuklären. Um den Mechanismus der CNT-basierten Nanodrahtschwingungen zu verstehen, untersuchen wir die zeitliche Entwicklung der geometrischen Phase im gequetschten Zustand, der ein klassisch ähnlicher Quantenzustand wie der kohärente Zustand ist. Der Vorteil des gequetschten Zustands besteht darin, dass die Unsicherheit einer Quadratur in diesem Zustand auf Kosten einer Erhöhung der Unsicherheit der anderen Quadratur erheblich reduziert werden kann, während eine solche Unsicherheitsmodulation im kohärenten Zustand unmöglich ist. Insbesondere werden wir die Auswirkungen der Resonanz auf die geometrische Phase analysieren. Da sich die Resonanzenergie deutlich von der Energie des nichtresonanten Zustands unterscheidet [22, 23], ist das topologische Verhalten der Wellenfunktion nicht trivial und kann von dem in normalen Situationen erheblich abweichen. Der Einfluss der Änderung physikalischer Parameter und der Quetschparameter auf die Entwicklung der geometrischen Phase wird ebenfalls gründlich analysiert. Die geometrischen Phasen sind in dynamischen Systemen allgegenwärtig [24] und können auf verschiedene moderne Technologien wie Quantencomputer [25], Intensitätsinterferometrie [26], photonisches Multitasking [27], Quantensensorprotokolle [28] und Welle -Stabilitätsmessungen [29].

Der Hamilton-Operator des Systems beinhaltet Zeitfunktionen, die mit der Dämpfung des Systems und der externen treibenden Kraft verbunden sind. Somit handelt es sich bei dem System um eine Art zeitabhängiger Hamilton-Systeme (TDHSs), deren quantenmechanische Probleme bis vor kurzem intensiv untersucht wurden. Die Zeitfunktion im Hamilton-Operator eines TDHS kann in den meisten Fällen nicht von der Funktion kanonischer Variablen getrennt werden, so dass die konventionelle Methode der Variablentrennung zur Lösung der Schrödinger-Gleichung nicht verfügbar ist. Eine alternative leistungsfähige Methode, die zur Überwindung dieser Schwierigkeit entwickelt wurde, ist die Methode der invarianten Operatoren, die von Lewis und Riesenfeld eingeführt wurde [30, 31]. Diese Methode ist ein sehr nützliches mathematisches Werkzeug, wenn wir Quantenlösungen eines TDHS ableiten. Viele quantenmechanische Probleme, die von TDHSs beschrieben werden, werden basierend auf dieser Methode untersucht. Dazu gehören beispielsweise chaotische Partikelstreuung [32], Lichtausbreitung in zeitveränderlichen Medien [33], Kontrolle eingefangener getriebener Elektronen [34] und Nichtklassizität quantennanoelektronischer Schaltkreise [35]. Es gibt eine Vielzahl anderer Methoden für die quantenmechanische Behandlung von TDHSs, darunter die unitäre Transformationsmethode [36], die algebraische Lie-Methode [37] und die Hamiltonsche Schätzungsmethode [38].

Da das System ein TDHS ist, verwenden wir die Methode des invarianten Operators, um Quantenlösungen des Systems zu erhalten. Ein linearer invarianter Operator, der durch den Annihilationsoperator repräsentiert wird, wird eingeführt. Während die Vernichtungs- und die Erzeugungsoperatoren aufgrund der Zeitabhängigkeit des Systems zeitlich dargestellt werden, können mit diesen Leiteroperatoren sowohl der kohärente als auch der gequetschte Zustand erhalten werden. Die geometrische Phase des Systems wird analytisch ausgewertet, indem die Wellenfunktion im gequetschten Zustand verwendet wird. Die zeitliche Entwicklung der geometrischen Phase wird anhand ihrer Darstellungen mit unterschiedlichen Parametern detailliert analysiert.

Methoden

Um die geometrische Phase zu untersuchen, müssen wir zunächst die klassische Bewegungsgleichung der Nanodrahtspitze aufstellen. Da die geometrische Phase in der Quantenwellenentwicklung eines TDHS auftritt, ist es notwendig, Wellenfunktionen in einem bestimmten Quantenzustand abzuleiten, den wir verwalten. Wir werden den gequetschten Zustand betrachten, wie im einleitenden Teil erwähnt. Die Wellenfunktionen in den verschiedenen Quantenzuständen eines TDHS, einschließlich des gequetschten Zustands, können mit der Methode des invarianten Operators erhalten werden.

Bewegungsgleichung für die zeitabhängige Amplitude x für einen Biegemodus einer suspendierten Kohlenstoff-Nanoröhrchen mit einer effektiven Masse m ist gegeben durch [1]

$$ \ddot{x}+\left(\frac{\omega_{0}}{Q} +\eta x^{2}\right) \dot{x}+\left(\omega_{0}^{ 2}+\beta x^{2}\right) x =f_{\mathrm{d}}\cos (\omega t), $$ (1)

wo ω ₀ ist die Resonanzkreisfrequenz, Q der Qualitätsfaktor, f _d die elektrostatische Antriebskraft geteilt durch m , η der nichtlineare Dämpfungskoeffizient und β der Duffing-Parameter. Nehmen wir der Einfachheit halber an, dass die Verschiebung der Spitze relativ zur CNT-Drahtlänge ausreichend klein ist. Dann können wir die nichtlinearen Terme in Gl. (1), führt zu [2]

$$ \ddot{x}+\frac{\omega_{0}}{Q} \dot{x}+\omega_{0}^{2} x =f_{\mathrm{d}}\cos (\omega T). $$ (2)

Der Hamiltonoperator des Systems, das Gl. (2) ist gegeben durch

$$ \hat{H}=e^{-\gamma t} \frac{\hat{p}^{2}}{2m} +\frac{1}{2}me^{\gamma t} \left [\omega_{0}^{2} \hat{x}^{2} - 2f_{\mathrm{d}}\cos (\omega t)\hat{x}\right], $$ (3)

wo γ =ω ₀ /Q . Die klassische Lösung von Gl. (2) besteht aus einer komplementären Funktion X _c (t ) und eine bestimmte Lösung X _p (t ), die gegeben sind durch

$$\begin{array}{@{}rcl@{}} &&X_{c}(t)=X_{c,0}e^{-\gamma t/2}\cos(\Omega t+\varphi) , \end{array} $$ (4) $$\begin{array}{@{}rcl@{}} &&X_{p}(t) =X_{p,0}\cos (\omega t - \ Delta), \end{array} $$ (5)

wobei X _{c ,0} ist eine Konstante, $\Omega =\sqrt {\omega_{0}^{2} - \gamma^{2}/4}$, φ eine beliebige Phase ist und

$$\begin{array}{@{}rcl@{}} X_{p,0}&=&\frac{f_{\mathrm{d}}}{\sqrt{\left(\omega_{0}^ {2} -\omega^{2}\right)^{2} + \gamma^{2} \omega^{2}}}, \end{array} $$ (6) $$\begin{array} {@{}rcl@{}} \delta &=&\tan^{-1} \frac{\gamma \omega}{ \omega_{0}^{2} -\omega^{2}}. \end{array} $$ (7)

Die klassische Lösung im Impulsraum ist in ähnlicher Weise gegeben, wobei die Komplementärfunktion $P_{c} (t) =me^{\gamma t} \dot {X}_{c}(t)$ und die spezielle Lösung ist $P_{p} (t) =me^{\gamma t} \dot {X}_{p}(t)$. Um die geometrische Phase des Systems zu untersuchen, müssen wir zunächst Quantenlösungen herleiten. Beachten Sie, dass der Hamilton-Operator des in Gl. (3) ist explizit zeitabhängig. Um Quantenlösungen des Systems abzuleiten, verwenden wir die Methode des invarianten Operators [30, 31], die eine nützliche Methode ist, wenn wir ein solches zeitvariables System behandeln. Ein invarianter Operator $\hat{I}$ des Systems kann aus der Liouville-von-Neumann-Gleichung abgeleitet werden, die gegeben ist durch ${d\hat{I}}/{dt} ={\partial\hat {I}}/{\partial t} + \left [\hat{I},\hat{H}\right]/\left (i\hbar\right) =0$. Aus einer rigorosen Auswertung nach dem Einsetzen von Gl. (3) in diese Gleichung haben wir einen linearen invarianten Operator [34] der Form

$$ \hat{I} =\hat{A} e^{i\Omega t}, $$ (8)

wobei $\hat{A}$ der Vernichtungsoperator ist, der durch

. gegeben ist $$ \begin{ausgerichtet} \hat{A} =&\left(2\hbar m\Omega\right)^{-1/2} \left[ m\left(\Omega+ i\frac{\gamma}{ 2} \right) e^{\gamma t/2}\left[\hat{x}-X_{p}(t)\right]\right.\\ &\left.+ie^{-\gamma t /2} \left[\hat{p}-P_{p}(t)\right]\! {\vphantom{\left(\Omega+i\frac{\gamma}{2}\right)}}\right]. \end{ausgerichtet} $$ (9)

Der hermitesche Adjungierte von Gl. (9), $\hat{A}^{\dagger}$, ist der Erzeugungsoperator.

Wir können die Eigenwertgleichung von $\hat{A}$ ausdrücken als

$$ \hat{A} |A \rangle =A |A \rangle. $$ (10)

Durch Auswertung der obigen Gleichung erhalten wir den Ausdruck des Eigenwerts mit

$$ A(t) =A(0) e^{-i\Omega t}, $$ (11)

wo A (0)=A ₀ e ^{−i φ} mit

$$ A_{0} =\left[m\Omega/(2\hbar)\right]^{1/2}X_{c,0}. $$ (12)

Während der kohärente Zustand |A 〉 ist der Eigenzustand von $\hat{A}$, der gequetschte Zustand ist der Eigenzustand eines Operators $\hat{B}$, der gegeben ist durch

$$ \hat{B} =\mu\hat{A} + \nu\hat{A}^{\dagger}, $$ (13)

wobei μ und ν sind komplexe Variablen, die die Gleichung

. ergeben $$ |\mu|^{2} - |\nu|^{2} =1. $$ (14)

Schreiben wir die Eigenwertgleichung von $\hat{B}$ in der Form

$$ \hat{B} |B \rangle =B |B \rangle, $$ (15)

|B 〉 ist der gequetschte Zustand. Durch Lösen dieser Gleichung im Konfigurationsraum haben wir

$$ {\begin{ausgerichtet} \langle {x}|B\rangle =&^{4}\!\!\!\sqrt{\frac{m \Omega e^{\gamma t}}{\hbar\ pi(\mu-\nu)(\mu^{*}-\nu^{*})}} \exp \left\{- \frac{1}{\hbar (\mu-\nu)} \left [\frac{1}{2} ich^{\gamma t}\left({\vphantom{\frac{1}{2}}}(\mu+\nu)\Omega\right.\right.\right. \\ &\left.+\frac{i\gamma}{2}(\mu-\nu)\right)\left[x-X_{p}(t)\right]^{2} -[iP_{ p}(t)(\mu-\nu)+\left(2\hbar m\Omega e^{\gamma t}\right)^{1/2} \\ &\left. \left.\times(\mu A+\nu A^{*}) ]\left[x-X_{p}(t)\right] {\vphantom{\frac{1}{2} me^{\gamma t}}}\right]-\frac{|A|^{2}+A^{2}}{2(\mu-\nu)(\mu^{*}-\nu^{*})} \Rechts\}. \end{aligned}} $$ (16)

Somit wurde die Wellenfunktion im gequetschten Zustand wie in Gl. (16). Auf der Grundlage einer solchen analytischen Beschreibung der Wellenfunktion können Quanteneigenschaften des Systems geklärt werden. Für μ =1 und ν =0, Gl. (16) reduziert sich auf die Wellenfunktion im kohärenten Zustand, der der Eigenzustand von Gl. (10) im Konfigurationsraum. Die Wellenfunktion, Gl. (16), wird im nächsten Abschnitt verwendet, um die geometrische Phase im gequetschten Zustand abzuleiten.

Ergebnisse und Diskussion

Es ist bekannt, dass die Phase in der Quantenwellenentwicklung sowohl die geometrische als auch die dynamische Phase umfasst. Die geometrische Phase wurde erstmals 1984 von Berry [12] für ein sich zyklisch entwickelndes System mit adiabatischer Änderung entdeckt. Nach dem adiabatischen Theorem der Quantenmechanik bleibt ein momentaner Eigenzustand eines Quantenzustands in einer zyklischen Entwicklung im Parameterraum später auf demselben Zustand, während es eine zusätzliche Akkumulation der Quantenphase, der Berry-Phase, gibt. Eine Verallgemeinerung der Berry-Phase in der Weise, dass sie die nichtadiabatische, nichtzyklische und/oder nicht-unitäre Evolution des Quantensystems umfasst, ist die geometrische Phase.

Die geometrische Phase im gequetschten Zustand ist gegeben durch

$$ \gamma_{G}(t) =\int_{0}^{t} \langle B(t') |i\frac{\partial}{\partial t'}| B(t')\rangle dt'+\gamma_{G}(0). $$ (17)

Die Differenzierung der Wellenfunktion nach der Zeit im Konfigurationsraum wird zu

$$ \frac{\partial \langle {x}|B\rangle}{\partial t} \,=\, \left\{ f_{1}(t) \!\left[x-X_{p}( t)\right]^{2}\,+\,f_{2}(t) \left[x\,-\,X_{p}(t)\right]\,+\,f_{3}( t) \rechts\}\! \!\langle {x}|B\rangle, $$ (18)

$$ f_{1}(t) =- \frac{m\gamma e^{\gamma t}}{2\hbar (\mu-\nu)} \left((\mu+\nu)\Omega + \ frac{i\gamma}{2}(\mu-\nu)\right), $$ (19) $$ {\begin{ausgerichtet} f_{2}(t) &=\frac{1}{\hbar (\mu-\nu)}\left[ \left((\mu+\nu)\Omega + \frac{i\gamma}{2}(\mu-\nu) \right) P_{p}(t) -ime^{\gamma t} \right.\\ &\quad\times\left[\omega_{0}^{2} X_{p}(t) - f_{\mathrm{d}} \cos(\ omega t)\right](\mu-\nu) +\left(2\hbar m\Omega e^{\gamma t}\right)^{1/2} \\ &\quad \left.\times\ left(\frac{\gamma}{2}\left(\mu A + \nu A^{*}\right)-i\Omega \left(\mu A - \nu A^{*}\right) \ rechts) \right], \\ \end{aligned}} $$ (20) $$ {\begin{aligned} f_{3}(t) &\!=\frac{\gamma}{4}-\frac {1}{\hbar me^{\gamma t}(\mu-\nu)} \left[iP_{p}(t)(\mu-\nu) + \left(2\hbar m\Omega e^ {\gamma t}\right)^{1/2} \right.\\ &\quad\left.\times\left(\mu A+\nu A^{*}\right){\vphantom{\left( 2\hbar m\Omega e^{\gamma t}\right)^{1/2}}}\right] P_{p}(t)+\frac{i\Omega A^{2}}{(\ mu-\nu)\left(\mu^{*}-\nu^{*}\right)}. \end{aligned}} $$ (21)

Weitere Auswertung nach Einsetzen von Gl. (18) in Gl. (17) gibt

$$ {\begin{ausgerichtet} \gamma_{G}(t) =&\int_{0}^{t} dt' \left[ A_{0}^{2}\left(\frac{\gamma^{ 2}}{4\Omega}+\Omega + g_{1} \sin\left[2\left(\Omega t'+\varphi\right)\right] +g_{2} \cos\left[2\ left(\Omega t'+\varphi\right)\right] \right) \right.\\ &\left.-A_{0}\left[ g_{3}(t') \sin\left(\Omega t'+\varphi\right) +g_{4}(t') \cos\left(\Omega t'+\varphi\right) \right]+g_{5}(t') {\vphantom{\frac {\gamma^{2}}{4\Omega}}}\right] +\gamma_{G}(0), \end{aligned}} $$ (22)

$$\begin{array}{*{20}l} g_{1}~ &=\frac{\gamma}{2} + \frac{i\Omega \left(\mu\nu^{*}-\ mu^{*}\nu\right)}{(\mu-\nu)\left(\mu^{*}-\nu^{*}\right)}, \end{array} $$ (23) $$\begin{array}{*{20}l} g_{2}~ &=\frac{\gamma^{2}}{4\Omega}+\Omega\frac{2|\nu|^{2 }- \left(\mu\nu^{*}+\mu^{*}\nu\right)}{(\mu-\nu) \left(\mu^{*}-\nu^{*} \right)}, \end{array} $$ (24) $$\begin{array}{*{20}l} g_{3}(t) &=\left(\frac{2\Omega}{m \hbar e^{\gamma t}} \right)^{1/2}P_{p}(t), \end{array} $$ (25) $$ {\begin{aligned} g_{4}( t) =\frac{1}{\sqrt{2\hbar\Omega}}\left(\frac{\gamma }{\sqrt{me^{\gamma t}}}P_{p}(t) - 2 \sqrt{me^{\gamma t}}\left[\omega_{0}^{2} X_{p}(t) - f_{\mathrm{d}} \cos(\omega t)\right]\ rechts), \end{aligned}} $$ (26) $$ {\begin{aligned} g_{5}(t) &=\frac{P_{p}^{2}(t)}{\hbar me ^{\gamma t}}+\frac{\gamma^{2}}{8\Omega}\left[2|\nu|^{2}-\left(\mu\nu+\mu^{*}\ nu^{*}\right) +1\right] \\ &\quad +\frac{i\gamma}{4(\mu-\nu)\left(\mu^{*}-\nu^{* }\right)} \left[|\mu|^{2}\left(\nu^{2}-\nu^{*2}\right)-|\nu|^{2}\lef t(\mu^{2}-\mu^{*2}\right)\right.\\ &\quad\left.+ (2|\nu|^{2}+1)\left(\mu\ nu^{*}-\mu^{*}\nu\right) +(\mu-\mu^{*})(\nu-\nu^{*})\right]. \end{aligned}} $$ (27)

Der letzte Term in g ₅ das enthält (μ −μ ^∗ )(ν −ν ^∗ ) ist als Phase unzureichend, da es sich um eine rein imaginäre Zahl handelt. Daher entfernen wir diesen Begriff jetzt, indem wir mindestens einen von μ . auswählen und ν als echter Wert. Diese Abhilfe kann immer ohne Einschränkung der Allgemeinheit erfolgen, da nur die relative Phase zwischen μ und ν hat eher eine physikalische Bedeutung als ihre absoluten Phasen.

Aus der Ausführung der Integration in Gl. (22), wir haben

$$ {\begin{ausgerichtet} \gamma_{G}(t) &=A_{0}^{2}\left[\left(\frac{\gamma^{2}}{4\Omega}+\Omega \right)t + \frac{g_{1}}{\Omega}\sin(\Omega t+2\varphi) \sin(\Omega t) +\frac{g_{2}}{\Omega} \cos (\Omega t+2\varphi)\right.\\ &\quad\left.\times\sin(\Omega t) {\vphantom{\frac{\gamma^{2}}{4\Omega}}} \right]\!-A_{0}\left[ \left(\frac{2m\Omega}{\hbar} \right)^{1/2}\omega X_{p,0} \bar{g}_ {3}(t) +\sqrt{\frac{2m}{\hbar\Omega}}\frac{1}{4\omega^{2}+\gamma^{2}}\bar{g}_{ 4}(t) \right]\\ &\quad+ \bar{g}_{5}(t) +\gamma_{G}(0), \end{aligned}} $$ (28)

wobei $\bar{g}_{i}(t)~(i=3,4,5)$ gegeben ist durch

$$ \bar{g}_{i}(t) =G_{i}(t) -G_{i}(0), $$ (29)

mit

$$ {\begin{ausgerichtet} G_{3}(\tau) &=e^{\gamma\tau/2}\left(\frac{1}{4(\Omega+\omega)^{2}+\ gamma^{2}} \left\{2(\Omega+\omega)\sin[(\Omega+\omega)\tau+\varphi-\delta] \right.\right.\\ &\quad\left.+\ gamma \cos[(\Omega+\omega)\tau+\varphi-\delta] \right\}- \frac{1}{4(\Omega-\omega)^{2}+\gamma^{2}} \ { 2(\Omega-\omega) \\ &\quad\left.\left.\times\sin[(\Omega-\omega)\tau\,+\,\varphi\,+\,\delta]\ !+\gamma\cos[(\Omega-\omega)\tau\,+\,\varphi\,+\,\delta]\right\} {\vphantom{\frac{1}{4(\Omega+\ omega)^{2}+\gamma^{2}}}}\right),\\ \end{aligned}} $$ (30) $$ {\begin{aligned} G_{4}(\tau) &=e^{\gamma\tau/2}\left\{X_{p,0}\left\{\gamma\omega[ 2\omega\cos(\omega\tau-\delta)-\gamma\sin( \omega \tau-\delta)] -2\omega_{0}^{2} \right.\right.\\ &\quad\left.\times[2\omega\sin(\omega \tau-\delta )+\gamma\cos(\omega\tau-\delta)] {\vphantom{X_{p,0}}}\right\}+2f_{\mathrm{d}} [ 2\omega\sin(\omega \tau) \\ &\left.\left.\quad+\gamma \cos(\omega \tau)\right]{\vphantom{X_{p,0}}}\right\}, \\ \end{ausgerichtet }} $$ ( 31) $$ {\begin{ausgerichtet} G_{5}(\tau) &=\frac{m\omega^{2}}{2\hbar}X_{p,0}^{2} \frac{e ^{\gamma\tau}}{\gamma\left(4\omega^{2}+\gamma^{2}\right)}\left\{\gamma^{2}+4\omega^{2} -\gamma^{2} \cos[2(\omega\tau -\delta)]\right.\\ &\quad\left.-2\gamma\omega \sin[2(\omega \tau -\delta )] {\vphantom{\gamma^{2}+4\omega^{2} -\gamma^{2}}}\right\} +\frac{\gamma^{2} \tau}{8\Omega }\left[2|\nu|^{2}-\left(\mu\nu+\mu^{*}\nu^{*}\right)+1\right] \\ &\quad+\frac{i \gamma \tau}{4(\mu-\nu)\left(\mu^{*}-\nu^{*}\right)} \left[|\mu|^{2}\left(\nu ^{2}-\nu^{*2}\right)-|\nu|^{2}\left(\mu^{2}-\mu^{*2}\right)\right.\\ &\quad\left.+\left(2|\nu|^{2}+1\right)\left(\mu\nu^{*}-\mu^{*}\nu\right)\right]. \end{aligned}} $$ (32)

Damit haben wir die volle geometrische Phase im gequetschten Zustand ausgewertet, die durch Gl. (28) mit Gl. (23), (24) und (29)–(32).

Die zeitliche Entwicklung der geometrischen Phase ist in den Fign. 1, 2, 3 und 4. Aus Abb. 1 sehen wir, dass die geometrische Phase schwingt und die Einhüllende einer solchen Schwingung mit der Zeit zunimmt. Die Zunahme der Hüllkurve ist größer, wenn A ₀ ist groß. Das Schwingungsmuster wird allmählich unregelmäßig, wenn die Werte von μ und ν Zunahme. Außerdem wird die Amplitude der Schwingung mit der Zeit groß.

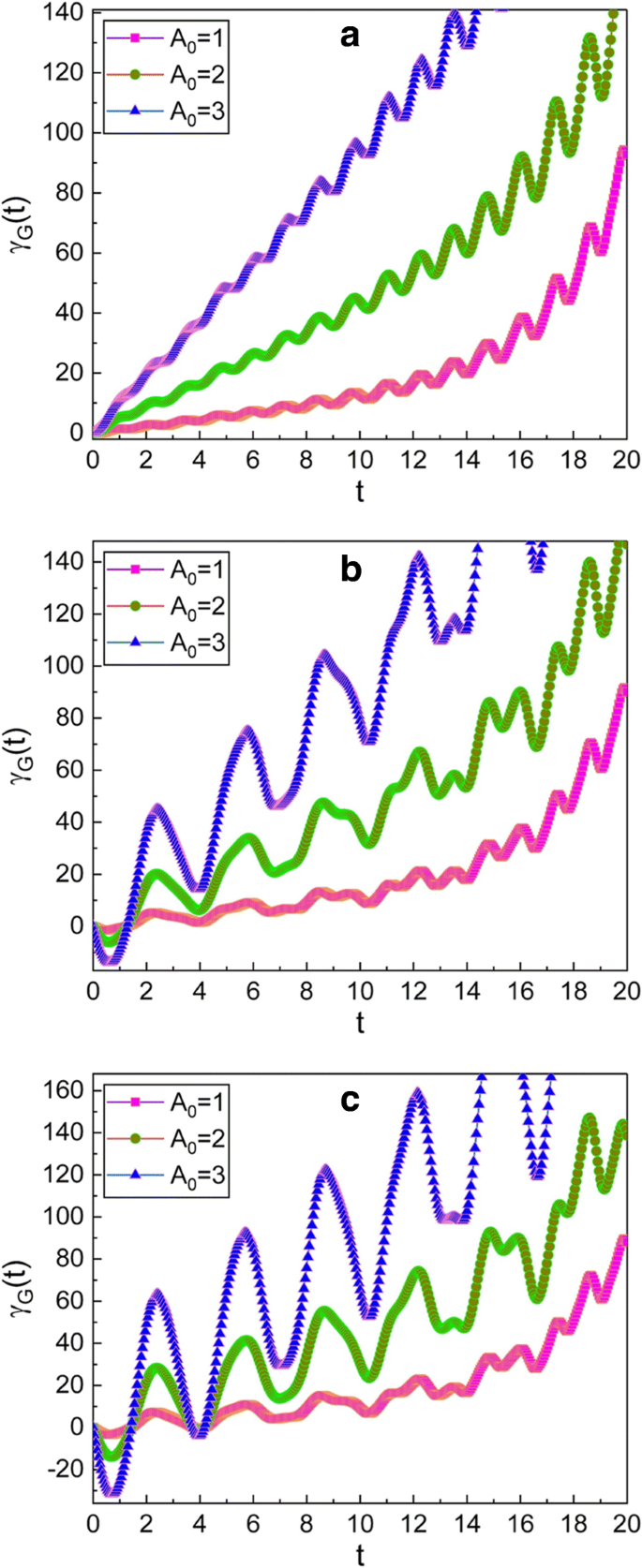
Zeitliche Entwicklung der geometrischen Phase für mehrere verschiedene Werte von A ₀ . Die Werte von (μ , ν ) in den Grafiken verwendet werden (1, 0) für a , ($\sqrt {2}$, 1) für b , und ($\sqrt {3}$, $\sqrt {2}$) für c . Wir haben m . verwendet =1, ω ₀ =1, ω =5, γ =0,35, f _d =1, $\hbar=1$, φ =0, und γ _G (0)=0. Die Phase und alle Parameter werden der Einfachheit halber als dimensionslos angenommen, und diese Konvention wird auch auf die nachfolgenden Figuren angewendet. Weil A ₀ wird in Form der klassischen Amplitude X . angegeben _{c ,0} der Komplementärfunktion [siehe Gl. (12)] können wir anhand der Grafiken bestätigen, dass die geometrische Phase groß ist, wenn die Schwingungsamplitude groß ist. Wir sehen auch, dass die Fluktuation von γ _G (t ) wird groß, wenn die Werte μ und ν unter der Bedingung in Gl. (14)

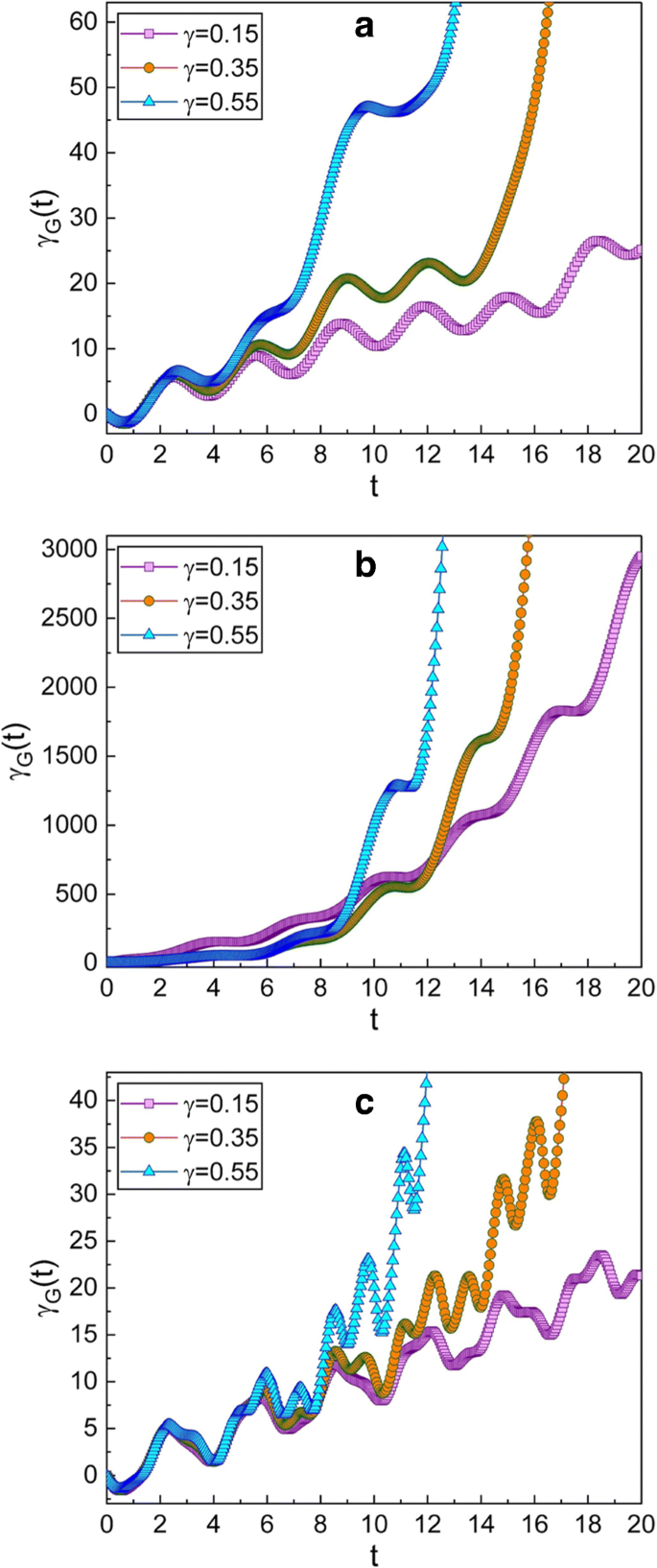
Zeitliche Entwicklung der geometrischen Phase für mehrere verschiedene Werte von γ . Der Wert von ω in den Grafiken verwendet ist 0,3 für a , 0,99 für b , und 5 für c . Die hier gewählten Quetschparameter sind $\mu =\sqrt {2}$ und ν =1; diese Wahl gibt q -Squeezed-Zustand bei der Anfangszeit. Andere Mengen, die wir verwendet haben, sind m =1, ω ₀ =1, A ₀ =1, f _d =1, $\hbar=1$, φ =0, und γ _G (0)=0. Wir bestätigen, dass die geometrische Phase groß ist, wenn der Dämpfungsfaktor γ ist in den meisten Fällen groß, aber nicht in allen. Die Häufigkeit des Falls b nahe der Resonanzfrequenz liegt, während die von a und c sind weit von der Resonanz entfernt. Die geometrische Phase für den Resonanzfall (b ) nimmt mit der Zeit sehr schnell zu

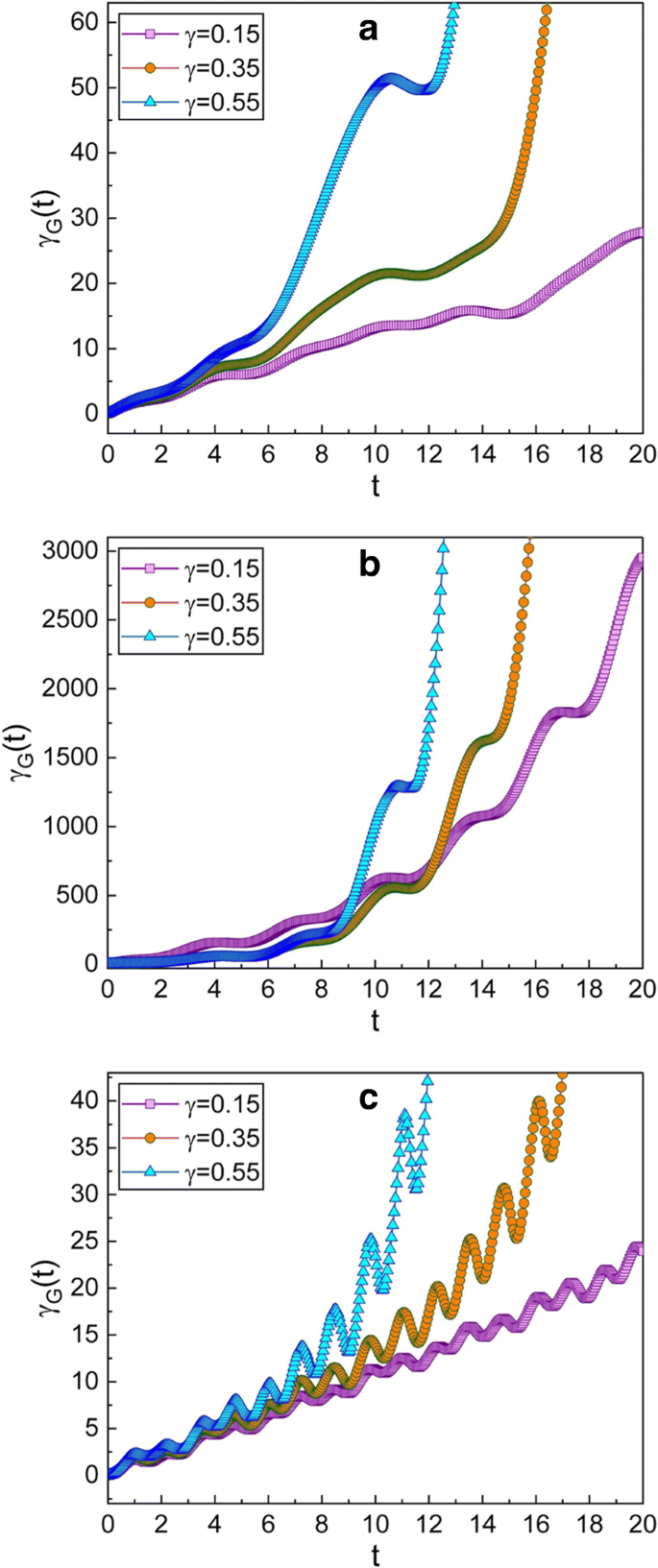
a –c Diese Grafik ist die gleiche wie in Abb. 2, aber für den Fall, dass die gewählten Quetschparameter $\mu =\sqrt {2}$ und ν . sind =−1 was ein p . ergibt -Squeezed-Zustand bei der Anfangszeit. Aus der Tatsache, dass sich die Gesamtgrafik in diesem Fall nicht so sehr von den entsprechenden in Abb. 2 unterscheidet, können wir bestätigen, dass die Entwicklung von γ _G (t ) ist für die Arten des Quetschens fast irrelevant, solange die Absolutwerte von μ und ν nicht ändern

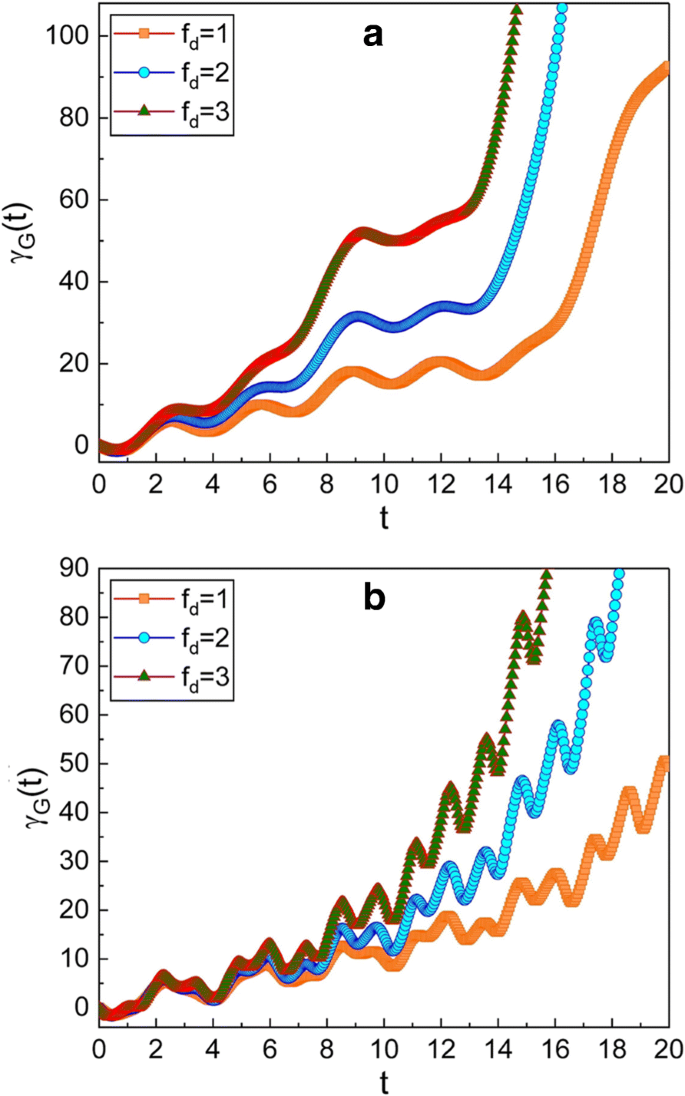
Zeitliche Entwicklung der geometrischen Phase für mehrere verschiedene Werte von f _d . Der Wert von ω in den Grafiken verwendet ist 0,3 für a und 5 für b . Wir haben $\mu =\sqrt {2}$, ν . verwendet =1, m =1, ω ₀ =1, γ =0,3, A ₀ =1, $\hbar=1$, φ =0, und γ _G (0)=0. Da die Amplitude (f _d ) der Antriebskraft steigt, die geometrische Phase wird groß

Die Squeezing-Effekte im Squeeze-Zustand in Abhängigkeit vom Squeeze-Parameter c wo c =μ /ν wurde in Lit. untersucht. [39]. Nach der Analyse in Lit. [39] (siehe Abb. 1(a) in Lit. [39]), der in Abb. 2 dargestellte gequetschte Zustand, der $c=\sqrt {2}$ entspricht, ist der q -Squeezed-Zustand zum Anfangszeitpunkt, während der in Abb. 3, der $c=-\sqrt {2}$ entspricht, der p . ist -gequetschter Zustand in der gleichen Situation. Durch den Vergleich der Abb. 2 und 3 zueinander, können wir schließen, dass die geometrische Phase im q -Squeezed-Zustand ist fast der gleiche wie im p -zusammengedrückter Zustand.

Die Auswirkungen von γ über die Entwicklung der geometrischen Phase kann aus den Fign. 2 und 3. Die geometrische Phase nimmt schneller zu, wenn γ ist groß. Durch den Vergleich der Abb. 2a und 3a mit den Fign. 2c und 3c können wir bestätigen, dass die geometrische Phase etwas schnell variiert, wenn ω größer als die Resonanzkreisfrequenz ist.

Das zeitliche Verhalten der geometrischen Phase bei oder nahe dem Resonanzzustand des Systems kann von großem Interesse sein [22, 23]. Die Abbildungen 2b und 3b zeigen, dass die geometrische Phase sehr schnell zunimmt, wenn ω nahe der Resonanzkreisfrequenz liegt. Dies bedeutet, dass die Wellenfunktion in dieser Situation mit der Zeit stark variiert, da die Größe der geometrischen Phase mit der zeitlichen Variation der Wellenfunktion zusammenhängt. Tatsächlich wird die Amplitude der Drahtschwingung im Resonanzzustand merklich erhöht. Übrigens sind die Resonanzkreisfrequenzen von suspendierten CNT-basierten Nanodraht-Resonatoren nicht nur hoch, sondern auch mit sehr hohen Gütefaktoren weitgehend abstimmbar [3]. Aus diesem Grund werden die Schwingungsmoden des Systems lange gehalten, bis sie vollständig gedämpft sind [11].

Abbildung 4 zeigt, dass die geometrische Phase auch von der Amplitude der treibenden Kraft f . beeinflusst wird _d . Als f _d erhöht, ist die Zunahme der geometrischen Zeitphase schnell.

Schlussfolgerung

Wir haben die geometrische Phase im gequetschten Zustand für das System auf Basis der Quantendynamik mit der Schrödinger-Gleichung untersucht. In Bezug auf die Zeitabhängigkeit des Hamilton-Operators, der das System beschreibt, wurde die Methode des invarianten Operators eingeführt, die ein potenzielles Werkzeug zur Ableitung von Quantenlösungen für den Fall ist, dass der Hamilton-Operator in Bezug auf die Zeit beschrieben wird. Mit dieser Methode wurde die analytische Formel der geometrischen Phase für die CNT-basierte Nanodraht-Oszillation erhalten.

Eine detaillierte Analyse der Phaseneffekte, die für ein theoretisches Verständnis der mechanischen Schwingungen notwendig ist, wurde durchgeführt. Unsere Entwicklung der geometrischen Phase ist eine vollständig quantenbasierte Entwicklung mit strengen mathematischen Auswertungen. Die geometrische Phase reagiert empfindlich auf die Änderung mechanischer Parameter und weist in vielen Fällen eine Schwingung auf. Der Einfluss der Quetschparameter auf die Entwicklung der geometrischen Phase wurde ebenfalls analysiert. Wir haben einen starken Anstieg der geometrischen Phasenakkumulation im Laufe der Zeit in der Nähe der Resonanzkreisfrequenz bestätigt.

Unsere Ergebnisse veranschaulichen das Zeitverhalten der geometrischen Phase, die in der Schwingung eines CNT-basierten Nanodrahts auftritt. Die Analyse der geometrischen Phase in dieser Arbeit ist wichtig, um nicht nur die topologischen Eigenschaften des Systems, sondern auch die dynamischen Schwingungen anderer mechanischer Oszillatoren auf Nanodrahtbasis zu verstehen. Insbesondere haben wir Phaseneigenschaften des Resonanzzustandes entwickelt, deren Klärung bei der Anwendung des Systems in Quanteninformationstechnologien und anderen quantenbasierten Industrien notwendig ist [40]. Die ähnliche Methode und der ähnliche Rahmen, der in dieser Forschung verwendet wird, können auch auf andere Nanosysteme wie supraleitende Fabry-Perot-Resonatoren [41], Nano-Cantilever [42] und Qubit-Resonator-Atom-Hybridsysteme [43] ausgedehnt werden.

Abkürzungen

CNT:: Kohlenstoff-Nanoröhrchen
EM-Wellen:: Elektromagnetische Wellen
TDHS:: Zeitabhängiges Hamilton-System

Direktes Wachstum einkristalliner GaN-Nanodrähte auf Indium-Zinn-Oxid-beschichtetem Siliziumdioxid Hochleistungs-U-Kanal-FETs mit rechteckigem Gate und nur 2 nm Abstand zwischen Source- und Drain-Kontakten

Nanomaterialien