Einfache Vektoraddition

Denken Sie daran, dass Vektoren mathematische Objekte sind, genau wie Zahlen auf einem Zahlenstrahl:Sie können addiert, subtrahiert, multipliziert und geteilt werden. Addition ist vielleicht die am einfachsten zu visualisierende Vektoroperation, also beginnen wir damit. Wenn Vektoren mit gemeinsamen Winkeln addiert werden, addieren sich ihre Größen (Längen) wie normale skalare Größen:(Abbildung unten)

Wenn Wechselspannungsquellen mit dem gleichen Phasenwinkel in Reihe geschaltet werden, addieren sich ihre Spannungen genauso, wie Sie es von Gleichstrombatterien erwarten würden:(Abbildung unten)

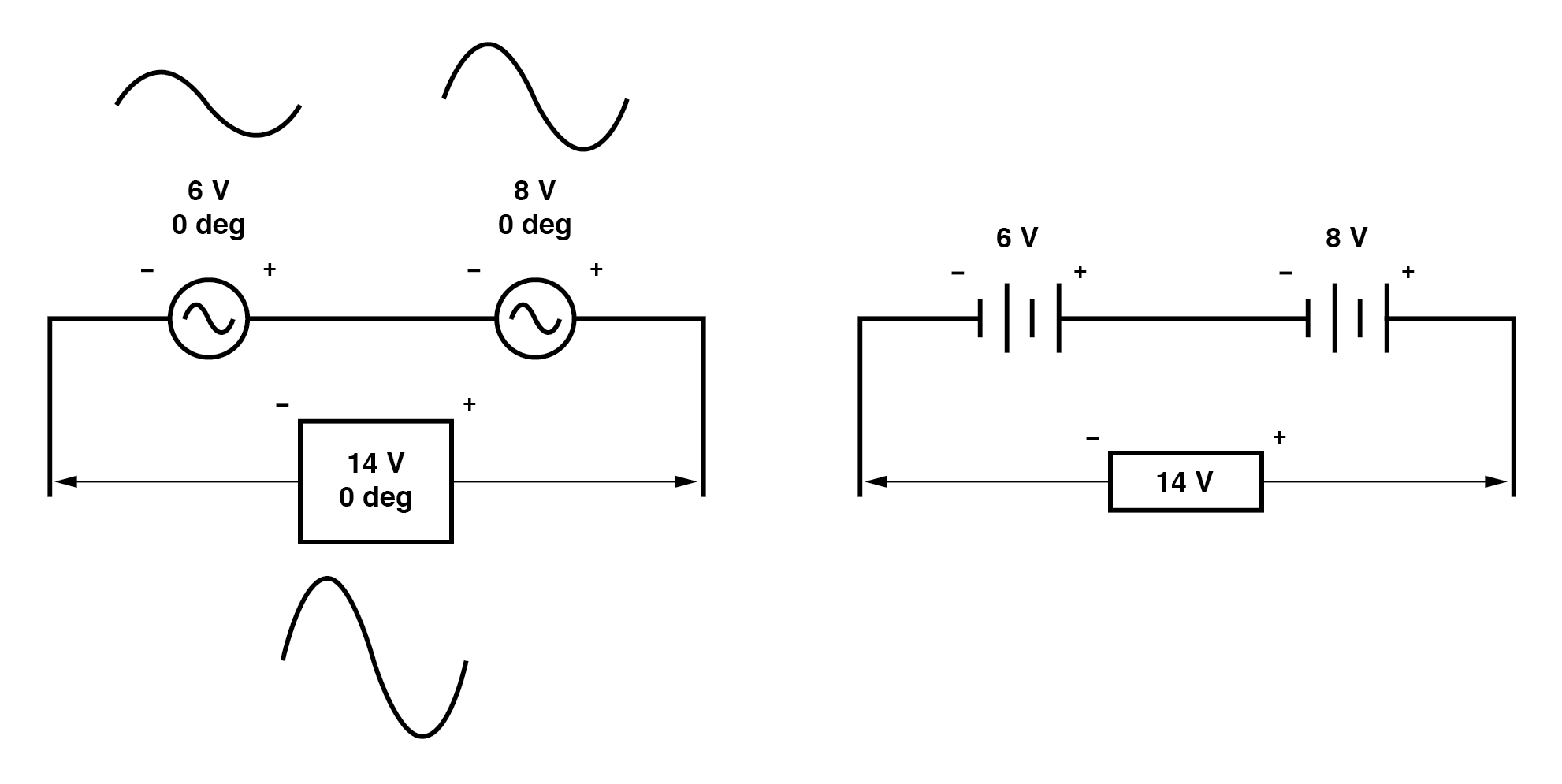
Bitte beachten Sie die (+) und (-) Polaritätsmarkierungen neben den Leitungen der beiden AC-Quellen. Obwohl wir wissen, dass Wechselstrom keine „Polarität“ im gleichen Sinne wie Gleichstrom hat, sind diese Markierungen wichtig, um zu wissen, wie die gegebenen Phasenwinkel der Spannungen zu beziehen sind. Dies wird im nächsten Beispiel deutlicher.

Wenn sich Vektoren direkt gegenüberstehen (180° phasenverschoben) werden addiert, ihre Größen (Längen) subtrahieren sich ebenso wie positive und negative skalare Größen subtrahieren, wenn sie addiert werden:(Abbildung unten)

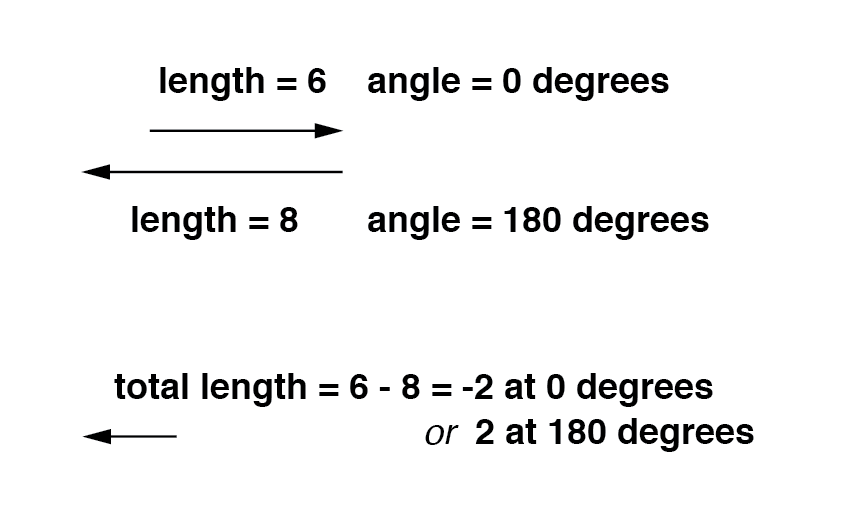
Wenn entgegengesetzte AC-Spannungsquellen in Reihe geschaltet sind, subtrahieren sich ihre Spannungen, wie Sie es bei gegenläufig angeschlossenen DC-Batterien erwarten können:(Abbildung unten)

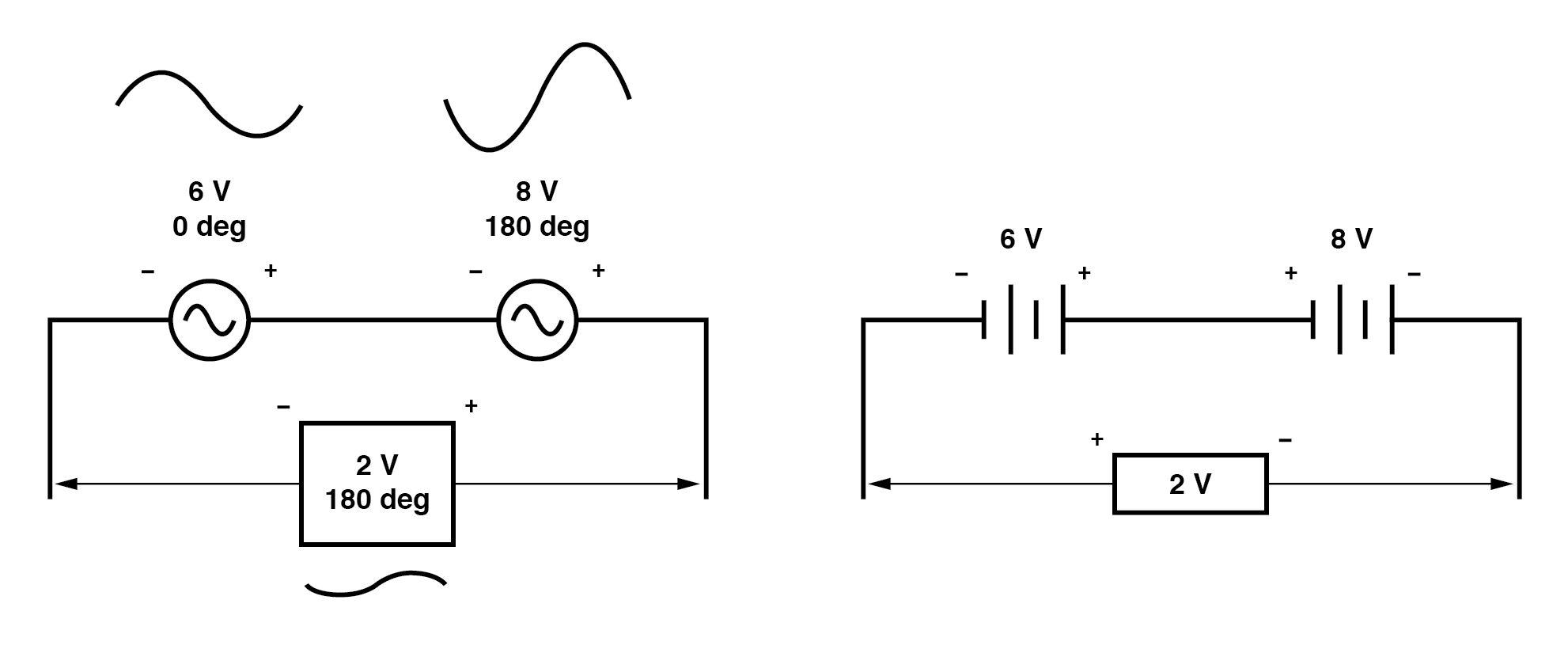
Um festzustellen, ob sich diese Spannungsquellen gegenüberstehen oder nicht, müssen ihre Polaritätsmarkierungen und . untersucht werden deren Phasenwinkel. Beachten Sie, wie die Polaritätsmarkierungen im obigen Diagramm additive Spannungen anzuzeigen scheinen (von links nach rechts sehen wir - und + an der 6-Volt-Quelle, - und + an der 8-Volt-Quelle).

Auch wenn diese Polaritätsmarkierungen normalerweise auf einen Zusatz hinweisen würden Effekt in einem Gleichstromkreis (die beiden Spannungen arbeiten zusammen, um eine größere Gesamtspannung zu erzeugen), in diesem Wechselstromkreis drücken sie tatsächlich in entgegengesetzte Richtungen, da eine dieser Spannungen einen Phasenwinkel von 0° . hat und das andere einen Phasenwinkel von 180° .

Das Ergebnis ist natürlich eine Gesamtspannung von 2 Volt.

Wir hätten die gegenläufigen Spannungen genauso gut in Reihe subtrahieren können wie folgt:(Abbildung unten)

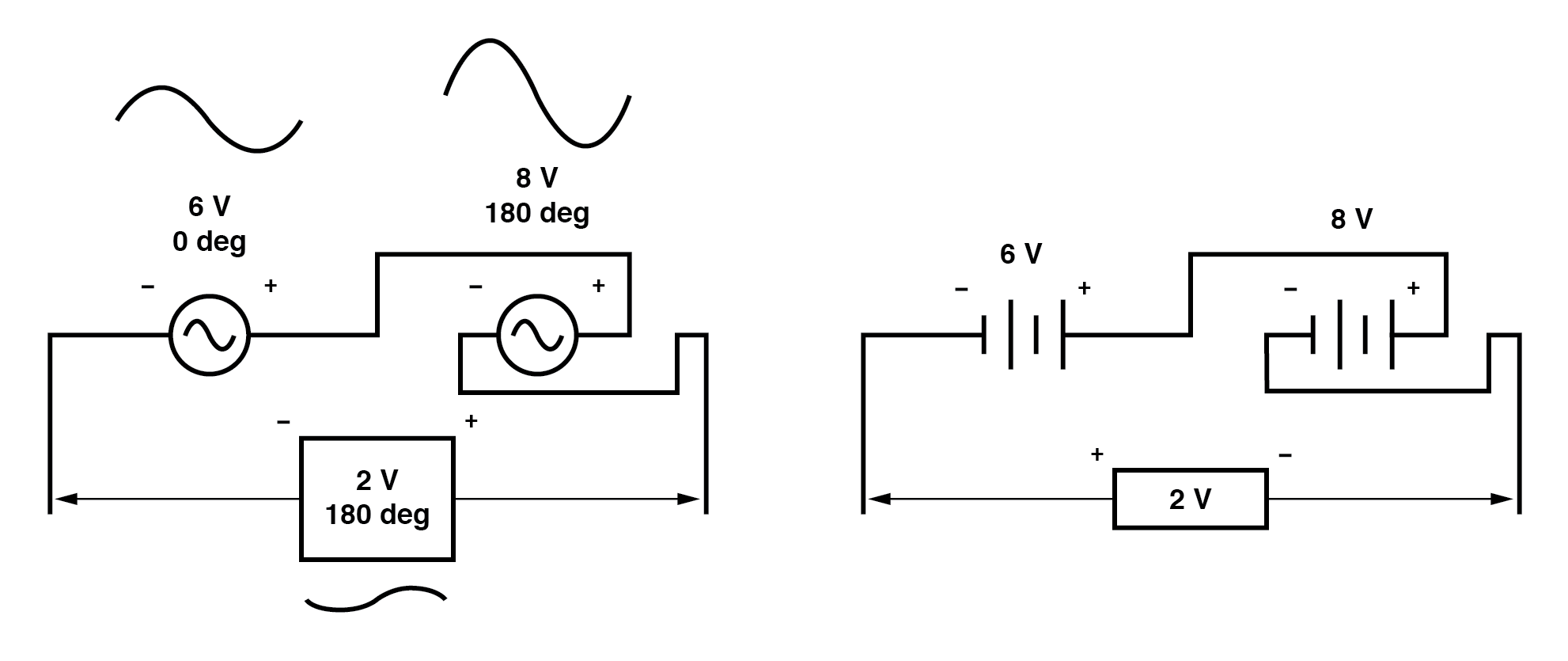
Beachten Sie, wie die Polaritäten jetzt aufgrund der Vertauschung der Drahtverbindungen an der 8-Volt-Quelle entgegengesetzt zu sein scheinen.

Da beide Quellen mit gleichen Phasenwinkeln beschrieben werden (0° ). (Abbildung unten)

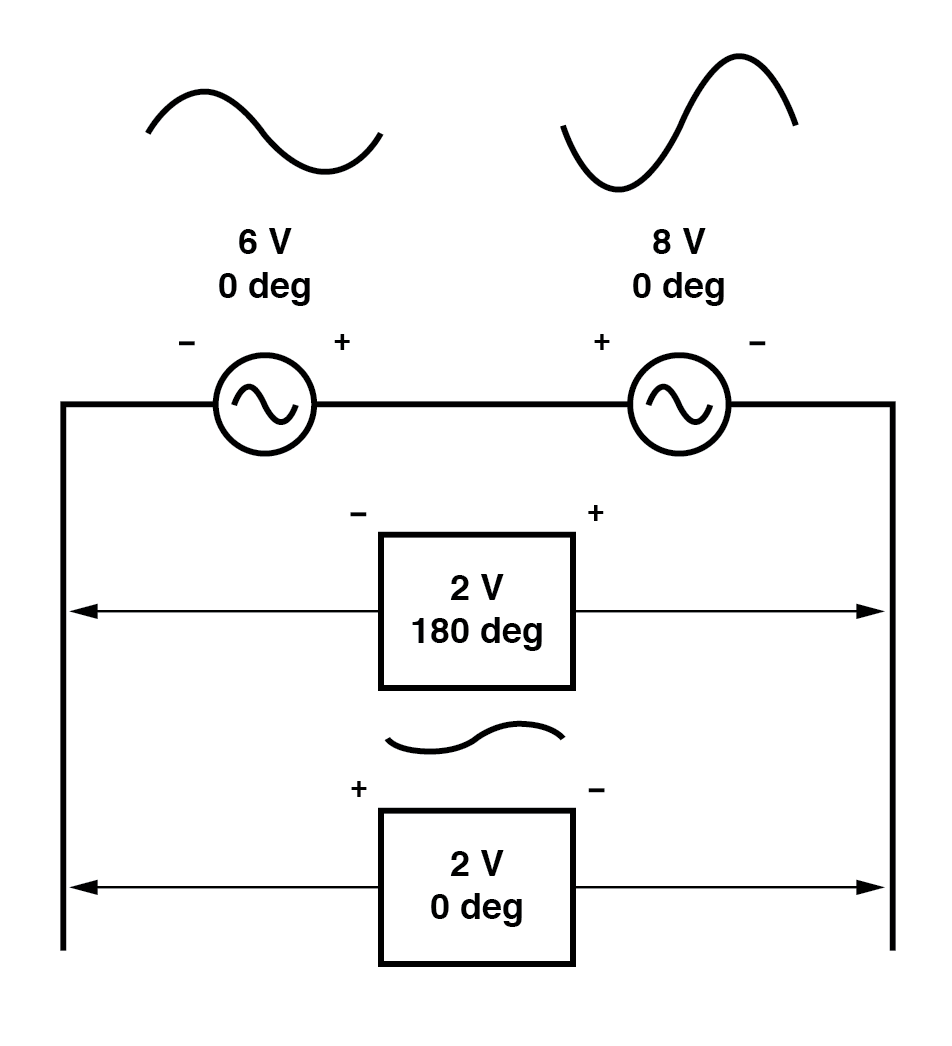
So wie es zwei Möglichkeiten gibt, die Phase der Quellen auszudrücken, gibt es zwei Möglichkeiten, das Ergebnis ihrer Summe auszudrücken.

Die resultierende Spannung kann auf zwei verschiedene Arten ausgedrückt werden:2 Volt bei 180° mit dem (-) Symbol links und dem (+) Symbol rechts oder 2 Volt bei 0° mit dem (+) Symbol links und das (-) Symbol rechts. Eine Vertauschung von Drähten von einer Wechselspannungsquelle entspricht einer Phasenverschiebung dieser Quelle um 180 °. (Abbildung unten)

Beispiel für äquivalente Spannungsquellen.

VERWANDTE ARBEITSBLÄTTER:

• Arbeitsblatt AC-Phase
• Arbeitsblatt zur AC-Netzwerkanalyse