AC-Phase

Die Dinge werden kompliziert, wenn wir zwei oder mehr Wechselspannungen oder -ströme in Beziehung setzen müssen, die nicht zueinander passen. Mit „außerhalb des Taktes“ meine ich, dass die beiden Wellenformen nicht synchronisiert sind:dass ihre Spitzen und Nullpunkte nicht zu den gleichen Zeitpunkten übereinstimmen. Die Grafik in der Abbildung unten veranschaulicht ein Beispiel dafür.

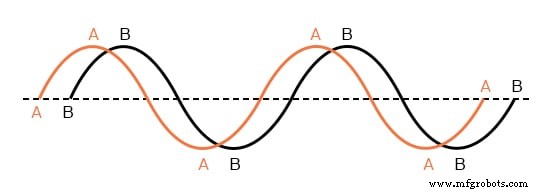
Phasenverschobene Wellenformen.

Die beiden oben gezeigten Wellen (A gegen B) haben die gleiche Amplitude und Frequenz, aber sie sind nicht aufeinander abgestimmt. In der Fachsprache wird dies als Phasenverschiebung bezeichnet . Zuvor haben wir gesehen, wie wir eine „Sinuswelle“ darstellen können, indem wir die trigonometrische Sinusfunktion für Winkel im Bereich von 0 bis 360 Grad berechnen, einen Vollkreis.

Der Startpunkt einer Sinuswelle war Null Amplitude bei Null Grad, schritt auf volle positive Amplitude bei 90 Grad fort, Null bei 180 Grad, vollständig negativ bei 270 Grad und zurück zum Startpunkt Null bei 360 Grad.

Wir können diese Winkelskala entlang der horizontalen Achse unseres Wellenformdiagramms verwenden, um auszudrücken, wie weit eine Welle von einer anderen abweicht:Abbildung unten

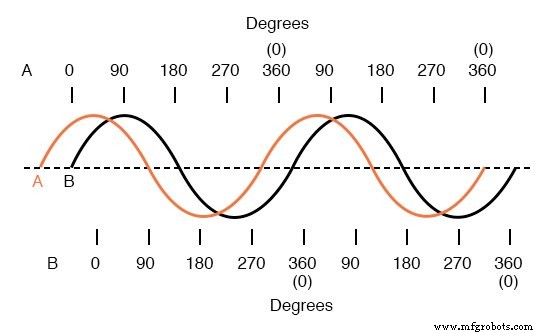
Welle A eilt Welle B um 45° voraus

Die Verschiebung zwischen diesen beiden Wellenformen beträgt etwa 45 Grad, wobei die „A“-Welle der „B“-Welle voraus ist. Eine Auswahl verschiedener Phasenverschiebungen wird in den folgenden Grafiken gezeigt, um dieses Konzept besser zu veranschaulichen:Abbildung unten

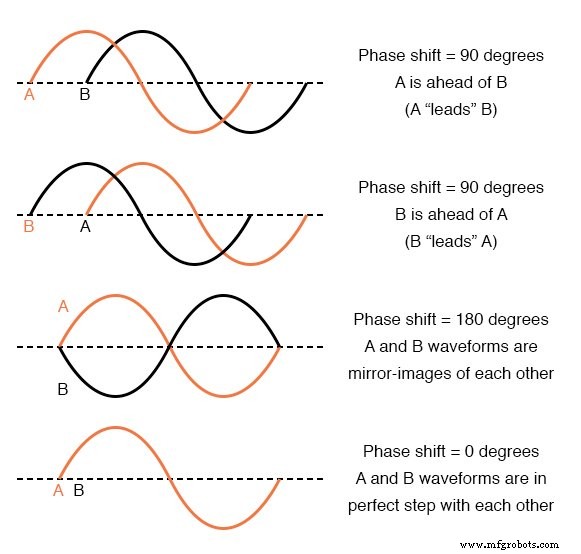
Beispiele für Phasenverschiebungen.

Da die Wellenformen in den obigen Beispielen dieselbe Frequenz aufweisen, sind sie zu jedem Zeitpunkt um den gleichen Winkelbetrag aus dem Takt geraten. Aus diesem Grund können wir die Phasenverschiebung für zwei oder mehr Wellenformen derselben Frequenz als konstante Größe für die gesamte Welle ausdrücken und nicht nur als Ausdruck der Verschiebung zwischen zwei bestimmten Punkten entlang der Welle.

Das heißt, man kann mit Sicherheit so etwas sagen wie "Spannung 'A' ist um 45 Grad phasenverschoben zu Spannung 'B'." Welche Wellenform auch immer in ihrer Entwicklung die Nase vorn hat, gilt als führend und der hintere soll nacheilend sein .

Die Phasenverschiebung ist wie die Spannung immer eine Messung relativ zwischen zwei Dingen. Es gibt wirklich keine Wellenform mit einem absoluten Phasenmessung, da keine universelle Referenz für die Phase bekannt ist.

Normalerweise wird bei der Analyse von Wechselstromkreisen die Spannungswellenform des Netzteils als Referenz für die Phase verwendet, die als "xxx Volt bei 0 Grad" angegeben wird. Bei jeder anderen Wechselspannung oder jedem anderen Wechselstrom in diesem Stromkreis wird die Phasenverschiebung relativ zu dieser Quellenspannung ausgedrückt.

Dies macht die Berechnung von Wechselstromkreisen komplizierter als Gleichstrom. Bei der Anwendung des Ohmschen Gesetzes und des Kirchhoffschen Gesetzes müssen die Größen der Wechselspannung und des Wechselstroms sowohl die Phasenverschiebung als auch die Amplitude widerspiegeln. Mathematische Operationen der Addition, Subtraktion, Multiplikation und Division müssen mit diesen Größen der Phasenverschiebung sowie der Amplitude arbeiten.

Glücklicherweise gibt es ein mathematisches Größensystem namens komplexe Zahlen ideal geeignet für diese Aufgabe der Darstellung von Amplitude und Phase.

Da das Thema komplexe Zahlen für das Verständnis von Wechselstromkreisen so wichtig ist, wird sich das nächste Kapitel ausschließlich diesem Thema widmen.

RÜCKBLICK:

• Phasenverschiebung ist, wo zwei oder mehr Wellenformen nicht zueinander passen.
• Der Betrag der Phasenverschiebung zwischen zwei Wellen kann in Grad ausgedrückt werden, wie durch die Gradeinheiten auf der horizontalen Achse des Wellenformdiagramms definiert, das beim Plotten der trigonometrischen Sinusfunktion verwendet wird.
• Ein führender Wellenform ist definiert als eine Wellenform, die in ihrer Entwicklung einer anderen voraus ist. Ein Rückstand Wellenform ist eine, die hinter einer anderen liegt. Beispiel:

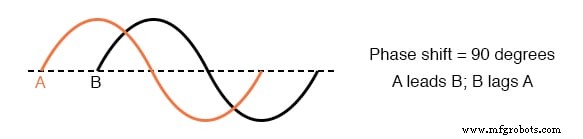
• Berechnungen für die Wechselstromkreisanalyse müssen sowohl die Amplituden- als auch die Phasenverschiebung der Spannungs- und Stromwellenformen berücksichtigen, um absolut genau zu sein. Dies erfordert die Verwendung eines mathematischen Systems namens komplexe Zahlen .

VERWANDTE ARBEITSBLÄTTER:

• Arbeitsblatt Trigonometrie für Wechselstromkreise