Was ist das Leistungsspektrum des Quantisierungsrauschens?

Unsere Serie zum Quantisierungsrauschen beginnt mit einer Erläuterung des Rahmens, den der Autor verwendet hat, um den Umfang seiner Untersuchungen zum Quantisierungsrauschen zu bestimmen.

Diese Serie ist eine Fortsetzung der Arbeit aus zwei vorangegangenen Serien. Zunächst wurde untersucht, ob die Kombination und Trennung von Inphase und Quadratur (I/Q) analog oder digital erfolgen sollte. Die Leistungsfähigkeit von I/Q-Modulatoren und -Demodulatoren sowie von Analog-Digital-Umsetzern (ADC) und Digital-Analog-Umsetzern (DAC) wurde untersucht. Wir haben auch diskutiert, was in diesem Zusammenhang eine gute Leistung einer Kommunikationsverbindung ausmacht.

ADCs und DAC werden als Datenwandler bezeichnet. Da nicht viele Informationen zu den Leistungsanforderungen von ADCs und DACs für moderne Kommunikationswellenformen gefunden wurden, beschloss Ihr Autor, sich mit diesen Problemen zu befassen. Die richtige Modellierung von ADCs und DACs wurde in der zweiten Reihe diskutiert, einschließlich Diskussionen über Modelle, die ENOB (effektive Anzahl von Bits) und ENOB plus ein Intermodulationspolynom verwenden. Wir haben auch den Vorschlag des Autors für ein noch effektiveres Modell besprochen, das einen Tiefpassfilter enthält.

Serienziel

Bei der Untersuchung der Leistung von Datenkonvertern wird häufig die in Abbildung 1 gezeigte Situation beobachtet.

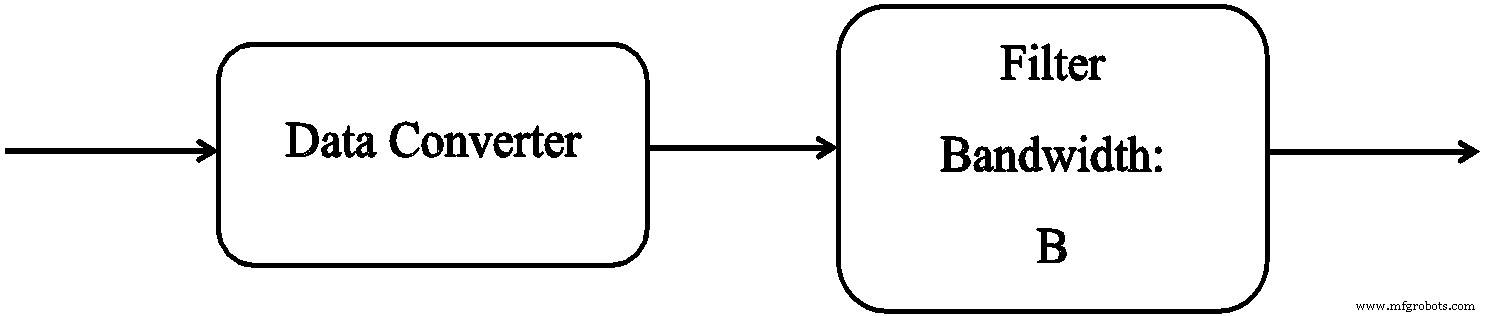
Abbildung 1. Vereinfachtes Blockdiagramm der Verwendung eines Datenkonverters

Die Gesamtrauschleistung des Datenwandlers in der Nyquist-Bandbreite (B_N ) ist N. Der Filter kann Bandpass oder Tiefpass sein, mit Bandbreite B_o . Normalerweise wird angenommen, dass die Rauschleistung des Filters:

Rauschleistung aus dem Filter =N(B_o / B_N )

Gleichung 1. Beachten Sie, dass diese Gleichung ungefähr für jeden vernünftigen Filter gilt, der dem ADC bei jeder Mittenfrequenz folgen könnte. Ein „angemessener Filter“ ist einer, der nicht zu eng ist.

Gleichung 1 geht davon aus, dass das Rauschen weiß oder gleichförmig mit der Frequenz ist.

Ihr Autor fragte sich; unter welchen Bedingungen ist diese Annahme, die oft als Pseudoquantisierungsrauschen [14]-Annahme bezeichnet wird, wahr?

Die Referenzen [3] bis [32] behandeln verschiedene Aspekte dieser Frage. Zur Verdeutlichung hat Ihr Autor auch einige Simulationen von Datenkonvertern mit verschiedenen Eingaben durchgeführt. Die Ergebnisse werden in dieser Serie berichtet.

Er betrachtete nur eine einheitliche Quantisierung (alle Schrittweiten gleich), da diese normalerweise in Hochgeschwindigkeits-Datenwandlern verwendet wird. Außerdem wurden Sigma-Delta-Wandler nicht berücksichtigt.

Bei ADC-Anwendungen wird die HF-Kettenverstärkung häufig so groß gewählt, dass das Rauschen von vorherigen Komponenten 3 bis 5 dB über dem Quantisierungsrauschen liegt, sodass das Quantisierungsrauschspektrum keine Rolle spielt. Dies kann jedoch die Systemkosten erhöhen, da eine höhere HF-Verstärkung und ein höherer Dynamikbereich vom ADC erforderlich sind.

Bei DAC-Anwendungen ist hoffentlich das Rauschen des DAC dominant, und man möchte später in der Kette kein Rauschen hinzufügen, nur um sicherzustellen, dass das übertragene Rauschspektrum weiß ist.

Spitzen-, Durchschnitts- und Effektivwerte

Es ist wichtig, den Pegel des Eingangssignals zu definieren. Abbildung 2 zeigt eine mit 5 Bit quantisierte Sinuswelle. Der Pegel dieses Signals wird normalerweise als 0 dBFS bezeichnet; wobei sich FS auf Full Scale auf dem Quantisierer bezieht. HF-Ingenieure befassen sich jedoch normalerweise mit Effektivgrößen. Da der Effektivwert einer Sinuswelle 3 dB unter dem Spitzenwert liegt, liegt die Sinuswelle in Abbildung 2 bei -3 dBrmsFS oder 0 dBpeakFS.

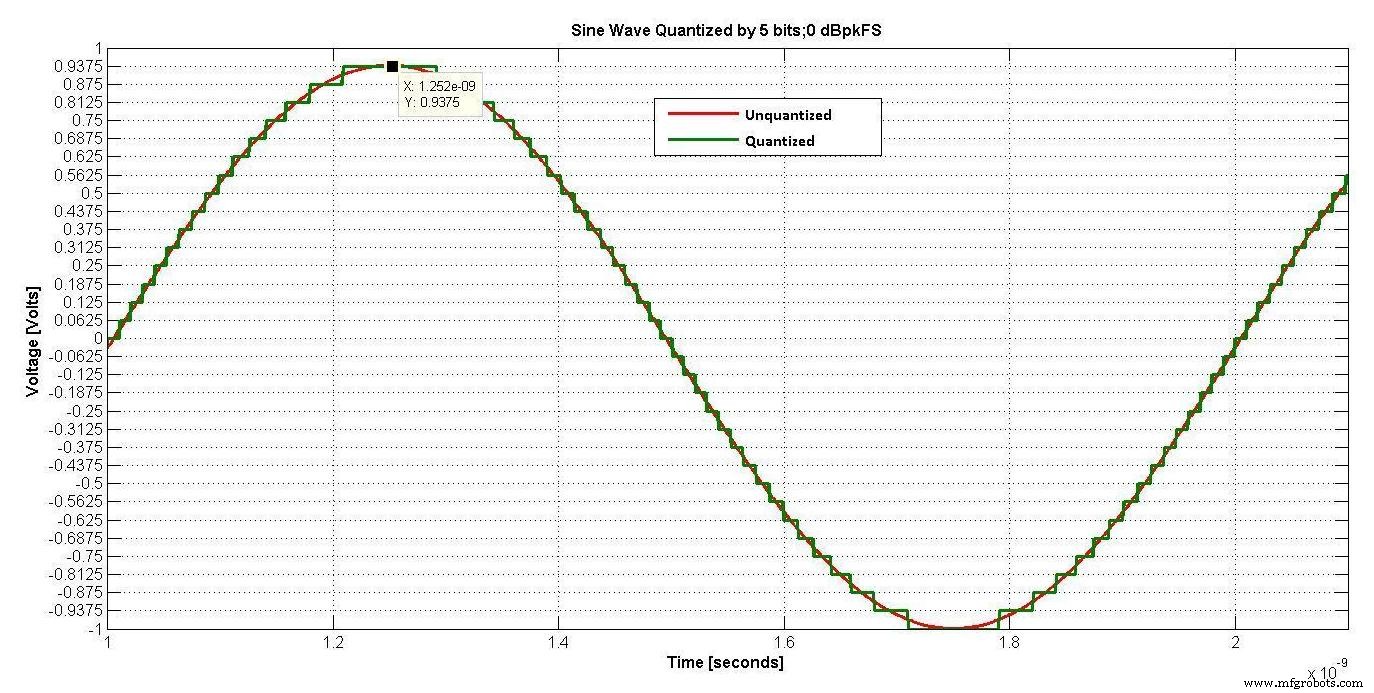
Abbildung 2.

Für den Rest dieser Serie werden die Signalpegel in dBrmsFS oder dBpeakFS angegeben,

Beachten Sie auch, dass das Spitzen-zu-Durchschnitts-Leistungsverhältnis (PAPR) dieser Sinuswelle mit konstanter Hüllkurve 3 dB beträgt, da die Leistung das Quadrat der Spannung ist. Tatsächlich beträgt der PAPR aller bandpassphasen- oder frequenzmodulierten Signale mit konstanter Hüllkurve, wie z. B. MSK, 3 dB.

"WARTE EINE MINUTE!" Sie könnten sagen, lieber Leser. „Ist das PAPR eines Signals mit konstanter Hüllkurve wie MSK nicht 0 dB? So nennen die Leute es.“

Wenn Leute auf diese Weise auf PAPR Bezug nehmen, beziehen sie sich auf das Verhältnis der Spitzenleistung der Hüllkurve zur durchschnittlichen Leistung der Hüllkurve. Insbesondere wird diese Bezugnahme auf PAPR verwendet, wenn die komplexe Hüllkurve [33] eines Signals charakterisiert wird. Da es sich in dieser Serie um reale Spannungen handelt, ist der PAPR die Leistung in der realen Spitze dividiert durch die Leistung im realen Durchschnitt. Dieser PAPR ist 3 dB höher als der normalerweise angegebene.

---

Im nächsten Artikel werden wir das Spektrum der Analog-Digital-Wandler (ADC)-Ausgänge besprechen.

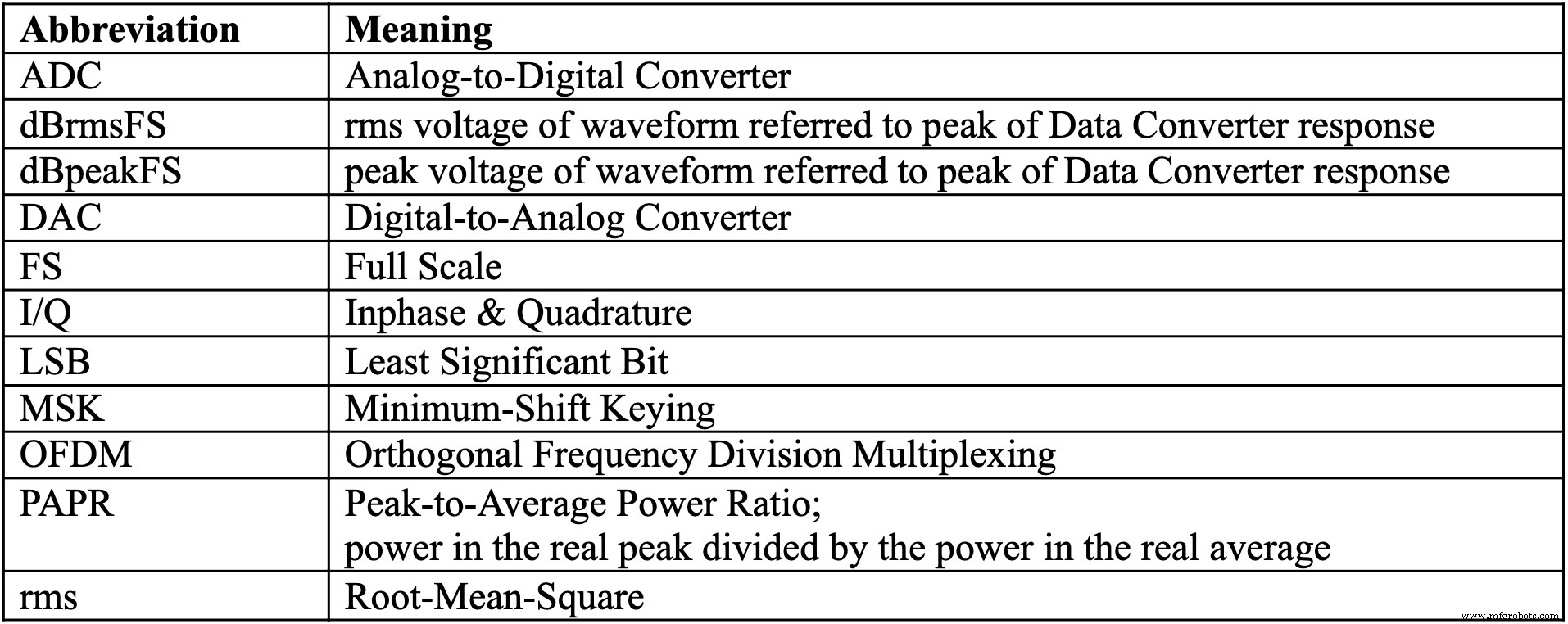
Verwendete Abkürzungen

Bitte verwenden Sie die folgende Tabelle für den Rest der Serie.

Referenzen

Die folgenden Referenzen werden auch im Rest der Serie verwendet:

Einführung und Motivation

[1] Digital oder analog? Wie sollte die Kombination und Trennung von I und Q erfolgen?

Voraussetzungen für eine gute Kommunikationsverbindungsleistung:IQ-Modulation und -Demodulation

[2] Wie sollten Datenkonverter für Systemsimulationen modelliert werden?

Modellieren von ADCs mit der effektiven Anzahl von Bits (ENOB)

Modellieren von ADCs mit Intermodulationspolynom und effektiver Bitanzahl

Hinzufügen eines Tiefpassfilters zu einem ADC-Modell und DAC-Modellierung

Quantisierungsrauschen mit oder ohne Clipping-Effekte

ADC und DAC

[3] Maloberti, Franco; Datenkonverter; Springer-Verlag; 2007

ADC-spezifisch, mit und ohne Clipping-Effekte

[4] Hebel, K. V.; Cattermol, K.W., "Quantising noise spectra", Electrical Engineers, Proceedings of the Institution of, Bd. 121, Nr. 9, S. 945,954, September 1974

Lever, K. V.; Cattermole, K.W., "Erratum:Quantising noise spectra", Electrical Engineers, Proceedings of the Institution of, Bd. 122, Nr. 3, S. 272, März 1975

[5] Gersho, A, "Principles of Quantization", Circuits and Systems, IEEE Transactions on, Bd. 25, Nr. 7, S. 427, 436, Juli 1978

[6] Gersho, A, "Quantization", Communications Society Magazine, IEEE, Bd. 15, Nr. 5, S. 16, 16. September 1977

[7] Schuchman, L., "Dither Signals and Their Effect on Quantization Noise", Communication Technology, IEEE Transactions on, Bd.12, Nr.4, S.162, 165, Dezember 1964

[8] Walden, R.H., "Analog-to-Digital Converters and Associated IC Technologies", Compound Semiconductor Integrated Circuits Symposium, 2008. CSIC '08. IEEE, Bd., Nr., S.1, 2, 12.-15. Okt. 2008

[9] Walden, R.H., „Performance trends for analog to digital converters“, Communications Magazine, IEEE, Bd. 37, Nr. 2, S. 96, 101, Feb. 1999

[10] Walden, RH, "Analog-to-Digital-Converter-Technologievergleich", Gallium Arsenide Integrated Circuit (GaAs IC) Symposium, 1994, Technical Digest 1994., 16th Annual, Bd., No., S. 217, 219, 16- 19. Okt. 1994

[11] Walden, R.H., "Analog-to-Digital Converter Survey and Analysis", Selected Areas in Communications, IEEE Journal on, Bd.17, Nr.4, S.539, 550, April 1999

[12] Morgan, Dr ,1016, Juli 1988

[13] Chow, P.E.-K., "Performance in Waveform Quantization", Communications, IEEE Transactions on, Bd. 40, Nr. 11, S. 1737, 1745, Nov. 1992

[14] Dardari, D., „Exakte Analyse der gemeinsamen Clipping- und Quantisierungseffekte in Hochgeschwindigkeits-WLAN-Empfängern“, Communications, 2003. ICC '03. IEEE International Conference on, Bd.5, Nr., S.3487, 3492 Bd.5, 11.-15. Mai 2003

[15] Gray, R.M., "Quantization noise spectra", Information Theory, IEEE Transactions on, Bd.36, Nr.6, S.1220,1244, Nov. 1990

[16] Echard, J.; Watt, M. L., "Das Quantisierungsrauschspektrum eines Sinusoids in farbigem Rauschen", Signal Processing, IEEE Transactions on, Bd. 39, Nr. 8, S. 1780, 1787, August 1991

[17] Er Jing; Li Gang; Xu Xibin; Yao Yan, "Estimation for the Quantization Noise Spectrum of Linear Digital Filter", Communication Technology Proceedings, 2000. WCC - ICCT 2000. International Conference on, Bd. 1, Nr., S. 184, 187 Bd. 1, 2000

[18] Bennett, W. R., "Spectra of quantiized signal", Bell System Technical Journal, The, Bd. 27, Nr. 3, S. 446, 472, Juli 1948

[19] Mohamed, EM, "Low Complexity Channel Estimation Technique for MIMO-Constant Envelope Modulation", Wireless Technology and Applications (ISWTA), 2013 IEEE Symposium on, vol., no., pp.97, 102, 22-25 Sept . 2013

[20] Clavier, A G.; Panter, P.F.; Grieg, D.D., "Distortion in a Pulse Count Modulation System", American Institute of Electrical Engineers, Transactions of the, Bd. 66, Nr. 1, S. 989, 1005, Jan. 1947

DAC-spezifisch, mit und ohne Clipping-Effekte

[21] Ling, W.A., "Shaping Quantization Noise and Clipping Distortion in Direct-Detection Discrete Multitone", Lightwave Technology, Journal of, Bd. 32, Nr. 9, S. 1750, 1758, 1. Mai 2014

Nur Clipping-Effekte; Nur ADC

[22] Mazo, JE, "Asymptotic Distortion Spectrum of Clipped, DC-biased, Gaussian Noise [optical communication]", Communications, IEEE Transactions on, Bd. 40, Nr. 8, S. 1339, 1344, August 1992

[23] Dakhli, M. C.; Zayani, R.; Bouallegue, R., "Eine theoretische Charakterisierung und Kompensation von nichtlinearen Verzerrungseffekten und Leistungsanalyse mit polynomialem Modell in MIMO OFDM-Systemen unter Rayleigh-Fading-Kanal", Computers and Communications (ISCC), 2013 IEEE Symposium on, vol., no., pp .000583.000587, 7.-10. Juli 2013

[24] Dardari, D.; Tralli, V.; Vaccari, A, "Eine theoretische Charakterisierung nichtlinearer Verzerrungseffekte in OFDM-Systemen", Communications, IEEE Transactions on, Bd. 48, Nr. 10, S. 1755, 1764, Okt. 2000

[25] Giannetti, F.; Lottici, V.; Stupia, I, "Theoretical Characterization of Nonlinear Distortion Noise in MC-CDMA Transmissions", Personal, Indoor and Mobile Radio Communications, 2006 IEEE 17. 2006

[26] Van Vleck, J. H.; Middleton, D., "The Spectrum of Clipped Noise", Proceedings of the IEEE, Bd. 54, Nr. 1, S. 2, 19. Januar 1966

Andere relevante mathematische Behandlungsmethoden

[27] Ermolova, N. Y.; Haggman, S.-G., "Eine Erweiterung der Bussgang-Theorie auf komplexwertige Signale", Signal Processing Symposium, 2004, NORSIG 2004. Proceedings of the 6th Nordic, vol., no., pp.45, 48, 11- 11. Juni 2004

[28] Requicha, Aristides AG, "Expected Values ​​of Functions of Quantized Random Variables", Communications, IEEE Transactions on, Bd.21, Nr.7, S.850,854, Juli 1973

[29] Pirskanen, J.; Renfors, M., "Quantization and jitter requirements in multimode mobile terminal", Communications, 2001. ICC 2001, IEEE International Conference on, Bd.4, Nr., S.1182, 1186 Bd.4, 2001

[30] Eisen, Fred H.; Riley, K. J.; Hummels, D. M.; Friel, G.A., "The noise power ratio-theory and ADC testing", Instrumentation and Measurement, IEEE Transactions on, Bd.49, Nr.3, S.659,665, Juni 2000

[31] Widrow, B., „A Study of Rough Amplitude Quantization by Means of Nyquist Sampling Theory“, Circuit Theory, IRE Transactions on, Bd. 3, Nr. 4, S. 266, 276, Dez. 1956

[32] Rowe, H. E., "Memoryless nonlinearities with Gaussian input:Elementary results", Bell System Technical Journal, The, Bd. 61, Nr. 7, S. 1519, 1525, Sept. 1982

[33] VanTrees, Harry L; Erkennungs-, Schätzungs- und Modulationstheorie, Teil III, Radar-/Sonarsignalverarbeitung und Gaußsche Signale im Rauschen; John Wiley und Söhne; 1971. Anhang:„Komplexe Darstellung von Bandpasssignalen, -systemen und -prozessen“ AES-1, Ausgabe:6, 1979, Seite(n):840 – 848.