Elektronische Struktur und I-V-Eigenschaften von InSe-Nanobändern

Hintergrund

Atomar dünne zweidimensionale (2D) Materialien haben in den letzten zehn Jahren aufgrund ihrer einzigartigen elektronischen Eigenschaften und vielversprechenden Anwendungspotenzials [1,2,3,4] hauptsächlich aufgrund ihrer reduzierten Dimensionalität großes Interesse auf sich gezogen. Eindimensionale (1D) Nanobänder können dann durch Maßschneidern der 2D-Materialien [5] oder durch präzises Anordnen von Atomen von unten nach oben hergestellt werden [6, 7]. In den Nanobändern werden die elektronischen Eigenschaften durch zusätzlichen Einschluss und mögliche Kantenfunktionalisierung weiter moduliert [8, 9]. Zum Beispiel kann ihre Energielücke, ein Schlüsselparameter von Halbleitern, durch ihre Breite kontinuierlich angepasst werden [10,11,12,13,14,15]. Die freien Bindungen der Kantenatome können durch H-Atome in der richtigen Umgebung passiviert werden, und die Hydrierung kann die Kanten vor der strukturellen Rekonstruktion stabilisieren [16, 17].

Vor kurzem wurde ein neues Mitglied, die InSe-Monoschicht, zu den 2D-Materialien hinzugefügt. Bulk-InSe gehört zur Familie der geschichteten Metallchalkogenid-Halbleiter und wurde in den letzten Jahrzehnten intensiv untersucht [18,19,20,21,22]. Jede seiner Vierfachschichten hat ein hexagonales Gitter, das effektiv aus vier kovalent gebundenen Se-In-In-Se-Atomebenen besteht. Die Vierfachschichten werden durch Van-der-Waals-Wechselwirkungen in einem Schichtabstand von etwa 0,8 nm zusammengestapelt. Der Stapelstil definiert seine Polytypen wie β, γ und ε, von denen die β- und γ-Typen direkte Bandlücken aufweisen. Dennoch wurde die einzelne vierfache InSe-Schicht erst in den letzten Jahren erfolgreich durch das mechanische Peeling-Verfahren hergestellt [23, 24]. Seitdem haben die beobachtete außergewöhnlich hohe Elektronenbeweglichkeit und die besonderen physikalischen Eigenschaften von InSe-Monoschichten umfangreiche Untersuchungen zu ihren möglichen Anwendungen in optoelektronischen Geräten [24,25,26] und elektronischen Geräten [27, 28] ausgelöst. Um neuartige funktionelle Eigenschaften zu erforschen, können auch theoretische Studien ein effizienter Ansatz sein. Numerische Simulationen der strukturellen, elektrischen und magnetischen Eigenschaften von InSe-Monoschichten und ihrer Modulation durch Dotierung, Defekte und Adsorption wurden durchgeführt [29,30,31,32,33,34,35,36,37,38]. Die Bandstrukturen von ein- und mehrschichtigem InSe wurden sorgfältig durch Dichtefunktionaltheorie untersucht [29]. Die dominanten intrinsischen Defekte in der InSe-Monoschicht wurden herausgefunden [30] und die Eigenschaften der nativen Defekte und der Substitutionsverunreinigungen in der InSe-Monoschicht wurden durch Berechnung der Bildungs- und Ionisierungsenergien [31] abgeschätzt. Darüber hinaus wurde vorhergesagt, dass eine Substitutionsdotierung von As-Atomen die InSe-Monoschicht von einem nichtmagnetischen Halbleiter auf einen magnetischen Halbleiter/Metall oder Halbhalbmetall übertragen kann [32]. Die Wärmeleitfähigkeit von InSe-Monoschichten kann durch ihre Größe stark moduliert werden [33]. Nach unserem besten Wissen gibt es jedoch bisher nur wenige Studien zu den elektronischen Eigenschaften von eindimensionalen Nanobändern von InSe-Monoschichten.

In diesem Artikel führen wir First-Principles-Simulationen zu den elektronischen Eigenschaften von 1D-freien Zickzack-, Sessel- und Klein-Monoschicht-InSe-Nanobändern und ihren wasserstoffpassivierten Gegenstücken durch. Unsere Studien zeigen den Übergang von Halbleiter zu Metall in wasserstoffpassivierten InSe-Zickzack-Nanobändern und die interessante Energielückenänderung in Sessel-Nanobändern. Die Strom-Spannungs-Kurven zeigen unterschiedliche elektrische Eigenschaften für Nanobänder mit unterschiedlichen Kanten.

Methoden

Dabei werden die drei typischen Kantenmuster Wabengitter, Zickzack (Z), Sessel (A) und Klein (K) berücksichtigt [39]. Wie in Abb. 1 dargestellt, kann ein Nanoband anhand seiner Breitenzahl n . identifiziert werden und die Kombination der Typen seiner beiden Kanten. Es gibt fünf Klassen von nackten Nanobändern:n -ZZ, n -AA, n -KK, n -ZK und n -KZ. Beachten Sie, dass n -ZK ist anders als n -KZ, weil wir annehmen, dass die linke (rechte) Z-Kante mit In (Se)-Atomen endet. Wenn jedes Kantenatom durch ein Wasserstoffatom passiviert wird, bezeichnen wir die passivierten Nanobänder als n -HZZH, n -HAAH, n -HKKH, n -HZKH und n -HKZH bzw. Eine Se-In-In-Se-Vierfachschicht der Gitterkonstanten 4,05 Å mit einem Se-In-Schichtabstand von 0,055 Å und einem In-In-Schichtabstand von 0,186 Å wird verwendet, um Nanobänder vor der Geometrieoptimierung herzustellen [21].

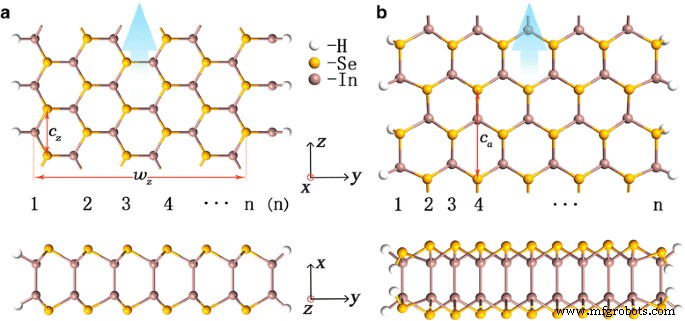
Draufsicht und Seitenansicht von 6-HZKH (a ) und 11-HAAH (b ) InSe-Nanobänder. Anzahl der Nanobandbreite n , Breite w _z , und Gitterkonstanten c _z oder c _a sind markiert

Alle Berechnungen werden mit dem Atomistix ToolKit (ATK) basierend auf DFT mit der Pseudopotentialtechnik durchgeführt. Das Austauschkorrelationsfunktional in der lokalen Spindichte-Approximation mit der Perdew-Zunger-Parametrisierung (LSDA-PZ) wird übernommen. Die Wellenfunktionen werden auf einem Basissatz von Doppel-ζ-Orbitalen plus einem Polarisations-Orbital (DZP) entwickelt. Ein Energiegrenzwert von 3000 eV, ein k -Raummaschengitter von 1 × 1 × 100 und eine elektronische Temperatur von 300 K werden bei der Realachsenintegration für die Nichtgleichgewichts-Green-Funktionen verwendet. Eine 15-Å dicke Vakuumschicht in den Superzellen wird verwendet, um die Nanobänder von ihren Nachbarbildern in beiden x . zu trennen und y Richtungen und die Unterdrückung der Kopplung zwischen ihnen sicherzustellen. Bandstrukturen werden nach vollständiger Geometrierelaxation mit einer Krafttoleranz von 0,02 eV/Å ⁻¹ . berechnet .

Um die elektronische Transporteigenschaft der Nanobänder zu simulieren, verbinden wir jedes einzelne zu einem Schaltkreis mit linkem (rechtem) chemischem Potential μ _L (μ _R ) [40, 41]. Das Nanoband kann dann in drei Regionen unterteilt werden, die linke (rechte) Elektrode L (R) und die zentrale Region C. Der spinabhängige Strom kann durch die Landauer-Büttiker-Formel abgeschätzt werden [42].

mit Spin σ =  ↑ , ↓ und Spannungsvorspannung V _b = (μ _R − μ _L )/e . Hier gilt \( {T}_{\sigma}\left(E,{V}_b\right)=Tr\left[{\Gamma}_L{G}_{\sigma }{\Gamma}_R{G} _{\sigma}^{\dagger}\right] \) ist das Transmissionsspektrum mit G _σ die retardierte Greensche Funktion in Region C und Γ _L (Γ _R ) die Kopplungsmatrix zwischen C und L (R). f _L (f _R ) ist die Fermi-Verteilungsfunktion der Elektronen in L (R).

Ergebnisse und Diskussion

In Abb. 1 zeigen wir die Draufsicht und die Seitenansicht von (a) 6-HZKH- und (b) 11-HAAH-Nanobändern mit Gitterkonstanten c _z = 4.05 Å und c _a = 7,01 Å. Kante K verläuft parallel zu der Richtung von Kante Z. Die Erstreckungsrichtung z des Nanobandes ist durch blaue Pfeile gekennzeichnet. Anders als bei Graphen-Nanobändern [39] wird für die drei Kantenstile sowohl bei bloßen als auch bei H-passivierten InSe-Nanobändern keine Kantenrekonstruktion beobachtet, und unsere Simulation zeigt, dass sie alle energetisch stabil sind.

Nackt n -ZZ-Nanobänder sind magnetische Metalle, mit Ausnahme des 2-ZZ, das eine rekonstruierte Geometrie hat und wie ein Halbleiter aussieht. Sie haben ähnliche Bandstrukturen wie in Fig. 2a dargestellt. Die p Orbitale von Se-Kantenatomen dominieren den Beitrag zu den Zuständen nahe der Fermi-Energie, ähnlich wie im Fall der InSe-Monoschicht [32], aber hier werden mehr Beiträge der In-Atome beobachtet. Die beiden teilweise besetzten Bänder stammen vom linken bzw. rechten Randzustand, wie durch die -Punkt-Bloch-Zustände für 4-ZZ-Nanoband gezeigt. Einer davon ist die Spinaufspaltung und ein magnetisches Nettomoment, z. B. 0,706 μ_B für 4-ZZ-Nanoband, erscheint in jeder primitiven Zelle am linken Rand.

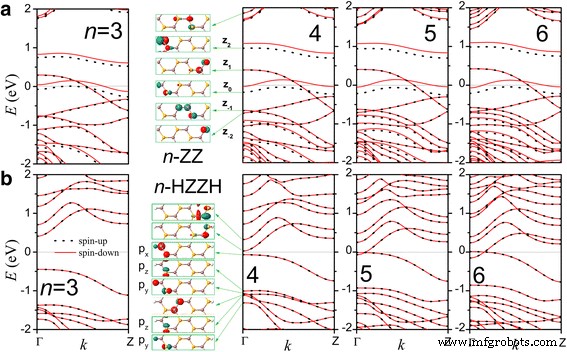
Die Bandstrukturen von a 3-, 4-, 5- und 6-ZZ-Nanobänder und b 3-, 4-, 5- und 6-HZZH-Nanobänder. Г-Punkt-Bloch-Zustände nahe der Fermi-Energie werden für n . gezeigt = 4 Die Bahnen der Zustände unterhalb der Fermi-Energie sind für 4-HZZH-Nanoband angegeben

Wenn die Randatome durch H-Atome passiviert werden, ist n -HZZH-Nanobänder werden für n . zu nichtmagnetischen Halbleitern = 3, 4 und Metall für n> 4 wie in Abb. 2b gezeigt. Beachten Sie, dass die Struktur für n . instabil wird =2. Im 4-HZZH-Nanoband sind die Bloch-Zustände bei Г in Leitungs-(Valenz-)Bändern nahe der Fermi-Energie auf den rechten (linken) Rand beschränkt. Sie haben Komponenten, die denen in 2D-InSe-Monoschichten ähneln, mit Ausnahme der H-Atomorbitalteile. Die höchsten fünf Bänder der linken Randzustände bestehen aus einem p _x , zwei p _y , und zwei p _z Orbitale von Se-Kantenatomen. Die Energiebänder der rechten (linken) Randzustände ähneln den Leitungsbändern (Valenz) in der Γ-K-Richtung der 2D-InSe-Monoschicht [32]. Ihre energetische Trennung hängt stark von n . ab obwohl ihre Dispersionen unempfindlich gegenüber n . sind . Wir definieren E _d als Energiedifferenz zwischen dem Minimum der rechten Randzustände und dem Maximum der linken Randzustände.

In Abb. 3 zeichnen wir E _d gegen n und w _z und fand ungefähr eine inverse Abhängigkeit E _d ≈ E ₀ + a /(w _z − w ₀ ) mit E ₀ =  − 0.45eV, w ₀ = 4Å und a = 4eVÅ. Dieses Verhalten ähnelt der Breitenabhängigkeit der Energielücke in Zickzack-Graphen und B-N-Nanobändern [12,13,14,15, 43,44,45,46,47] mit Ursprung der Elektron-Elektron-Wechselwirkung. Schmale HZZH-InSe-Nanobänder sind Halbleiter, und mit zunehmender Breite tritt ein Übergang von Halbleiter zu Metall auf.

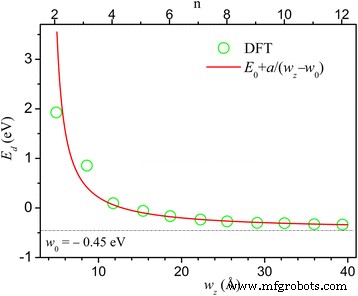
Die minimalen Energieunterschiede E _d zwischen dem rechten und linken Randzustand nahe der Fermi-Energie in n -HZZH-Nanobänder sind gegen n . gezeigt und w _z . Die Fitkurve ist rot

Die Bandstrukturen von n -KK und n -HKKH-Nanobänder reagieren nicht auf die Breitenzahl n wie in Abb. 4a bzw. b veranschaulicht für n =4. Im Vergleich zur Zickzack-Kante hat die blanke Klein-Kante mehr baumelnde Bindungen, was zu einer signifikanten Änderung der Bandstruktur führt. Orbitale von Rand-Se-Atomen haben normalerweise eine niedrigere Energie als die von Rand-In-Atomen, ähnlich dem ZZ-Nanoband. In HKKH-Nanobändern ist die Unterdrückung des p Orbital der Kante In Atomen und der p Orbital des Rand-Se-Atoms durch die Passivierung von H-Atomen ist offensichtlich. Dennoch reicht ein H-Atom nicht aus, um alle baumelnden Bindungen der Randatome zu passivieren. Sowohl KK- als auch HKKH-Nanobänder sind aus Metall.

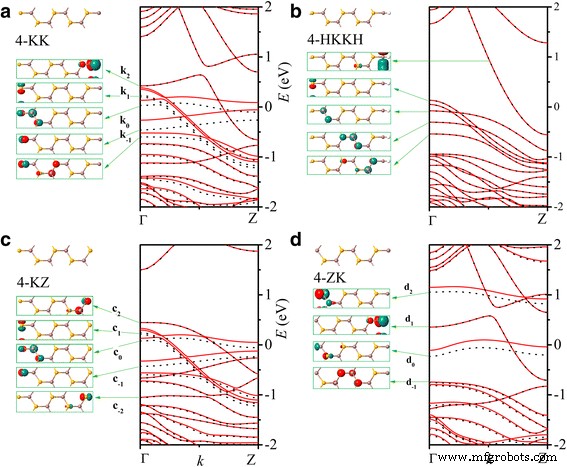
Die Bandstrukturen und Γ-Punkt-Bloch-Zustände von 4-KK (a ), 4-HKKH (b ), 4-KZ (c ) und 4-ZK (d ) Nanobänder

In Nanobändern mit einer Mischung aus Zickzack- und Kleinkanten beobachten wir eine Kombination von Energiebändern der beiden Kantenarten nahe der Fermi-Energie. Wie in Abb. 4c für das 4-KZ-Nanoband gezeigt, sind die Dispersion und die Γ-Punkt-Bloch-Zustände der Bänder c₁ , c₀ , und c₋₁ sind die gleichen wie die von Band k₁ , k₀ , und k₋₁ in 4-KK-Nanoband wie in Abb. 4a aufgetragen, während die Bänder c₂ und c₋₂ sind identisch mit Band z₁ und z₋₂ von 4-ZZ-Nanobändern in Abb. 2a. In ähnlicher Weise besteht die Bandstruktur des 4-ZK-Nanobands, wie in Fig. 4d dargestellt, aus Band d₁ von der rechten Kleinkante und Bänder d₂ , d₀ , und d₋₁ von der linken Zickzackkante. Seit n -ZK- und n-KZ-Nanobänder behalten einen Teil der Energiebänder von n -KK-Nanobänder in der Nähe der Fermi-Energie, sie sind beide aus Metall wie das n -KK Nanobänder. Aus dem gleichen Grund sind auch die Mischkanten Z und K der H-passivierten Nanobänder metallisch.

Sowohl die AA- als auch die HAAH-Nanobänder sind nichtmagnetische Halbleiter, wie in Abb. 5a, b gezeigt, wo die Bandstrukturen für n . aufgetragen sind = 4, 5. Die Passivierung von H-Atomen kann die strukturelle Stabilität energetisch verbessern und die Energielücke vergrößern. Interessanterweise hat die Energielücke eine Zickzack-Abhängigkeit von der Nanobandbreite, was ein ungerad-gerades familienähnliches Verhalten wie bei Graphen- und BN-Nanobändern zeigt [10,11,12,13,14,15, 43,44,45,46, 47]. Wie in Abb. 5c dargestellt, n -AA-Nanobänder haben eine schmalere Lücke (olivfarbenes Quadrat) als die von 2D-InSe-Monoschichten (roter Strich). Die Lücke wächst (verringert) sich monoton mit der Breite für ungerade (gerade) n und konvergiert auf einen Wert von 1,15 eV an der Grenze der großen Breite, wenn die beiden Kanten voneinander entkoppelt sind und ihre Energie stabilisieren [13]. Die Bloch-Zustände des Valenzbandmaximums (VBM) am Г-Punkt und des Leitungsbandminimums (CBM) am Z-Punkt sind auch in Abb. 5c gezeigt. Das Paritätsverhalten wird wieder mit dem symmetrischen (n = 5) oder diagonal (n = 4, 6) Verteilung der Zustände um Rand-Se-Atome bei VBM und um Rand-In-Atome bei CBM.

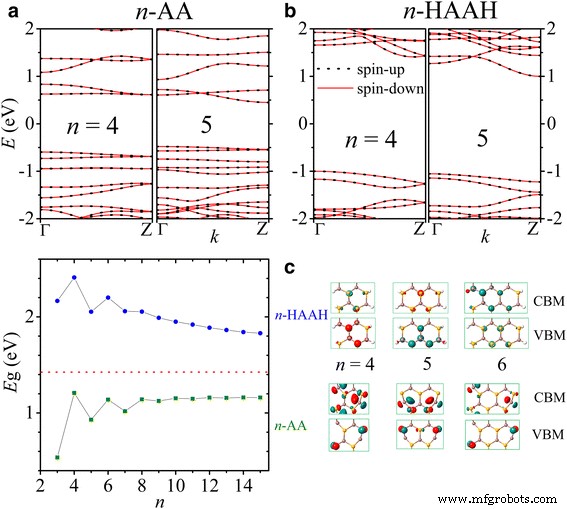
Die Bandstrukturen von 4- und 5-AA-Nanobändern sind in a . gezeigt und die von 4- und 5-HAAH in b . Die Energielücken E g von n -AA (grün) und n -HAAH (blau) Nanobänder sind gegen n . aufgetragen in c wobei die Lücke der InSe-Monoschicht (rot) markiert ist. Die Bloch-Staaten bei CBM und VBM für n = 4, 5 und 6 werden in den rechten Feldern von c . angezeigt

Andererseits sind die Lücken von n -HAAH-Nanobänder (blauer Kreis) sind breiter als ihr 2D-Gegenstück und nehmen mit der Breite sowohl für ungerade als auch für gerade n . ab . In passivierten Nanobändern haben die Bloch-Zustände bei VBM und CBM viel weniger Kantenkomponenten. Die entsprechenden Energielücken sind etwa 1 eV breiter als die der bloßen Nanobänder, und der Unterschied nimmt mit zunehmender Breite ab [13].

In Abb. 6a zeigen wir die Strom-Spannung (I -V ) charakteristisch für die obigen metallischen InSe-Nanobänder 4-ZZ (Quadrat), 4-KK (Kreis) und 4-HKKH (Dreieck). Spin-Up-(Spin-Down-)Kurven sind durch gefüllte (leere) Symbole gekennzeichnet. Zur Berechnung des spinabhängigen Stroms I . wurde die Landauer-Büttiker-Formel verwendet _σ wenn eine Vorspannung V _b wird zwischen den Elektroden L und R angelegt, mit μ _R = eV _b /2 und μ _L =  − eV _b /2 angenommen. Negativer differentieller Widerstand (NDR) und Spinpolarisation werden in 4-ZZ- und 4-KK-Nanobändern unter einer Vorspannung im Bereich zwischen 0,5 und 1,2 V beobachtet. Das Spitze-zu-Tal-Verhältnis von NDR ist größer als 10 für die 4- ZZ-Nanoband aufgrund der transversalen Fehlanpassung von Wellenfunktionen zwischen Energiebändern nahe der Fermi-Energie, wie in Abb. 2a dargestellt und im Folgenden erläutert. Band z₁ ist der dominante Transportkanal unter V _b < 1,2 V, wie durch die Spin-Up- und Spin-Down-Transmissionsspektren in Fig. 6b bzw. c angezeigt. Die Wellenfunktionen von Band z₁ sind orthogonal zu oder räumlich getrennt von denen benachbarter Bänder z₂ , z₋₁ , und z₋₂ . Dies führt zu der Diskrepanz zwischen den Zuständen z₁ an einer Elektrode und solche gleicher Energie an der anderen Elektrode unter V _b . Die Elektronen aus Band z₁ in einer Elektrode haben dann Schwierigkeiten, unter Energieerhaltung zur anderen Elektrode zu transportieren. Als Ergebnis ist das I-V Kurve von Nanoband 4-ZZ zeigt eine Einzelbandcharakteristik mit starkem NDR. Außerdem ist der Spin-Split von Band z₀ führt zur Spinpolarisation im linearen Regime. Im passivierten 4-HKKH-Nanoband sättigt sich der Strom jedoch im obigen NDR-Vorspannungsbereich.

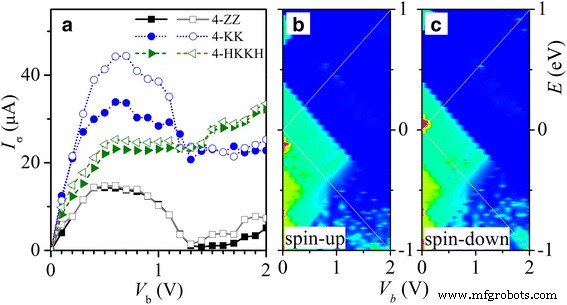
a Das Spin-Up (gefüllt) und das Spin-Down (leer) I -V Eigenschaften von 4-ZZ (Quadrat), 4-KK (Kreis) und 4-HKKH (Dreieck) InSe-Nanobänder werden vorgestellt. Die entsprechenden Transmissionsspektren des Spin-up (b ) und Spin-Down (c ) sind für das 4-ZZ-Nanoband gezeigt. Das Transportfenster zwischen μ _L und μ _R ist durch die weißen Linien gekennzeichnet

Schlussfolgerungen

Wir haben die elektronischen Eigenschaften von InSe-Nanobändern mit Z-, A- oder K-Kanten systematisch untersucht. Die Kanten spielen eine Schlüsselrolle bei der Bestimmung der Eigenschaften, da Elektronenzustände nahe der Fermi-Energie ein großes Gewicht von Kantenatomorbitalen haben. Blanke Z- und K-Kanten sind leitfähig und magnetisch. Starke Kanten-Kante-Wechselwirkung kann zum Übergang von n . führen -HZZH-Nanobänder vom Halbleiter zum Metall als n steigt. Als Ergebnis sind blanke und H-passivierte Nanobänder mit Z- und K-Kanten metallisch, außer sehr schmalen. n -AA und n -HAAH sind nichtmagnetische Halbleiter mit schmaleren bzw. breiteren Energielücken als die von InSe-Monoschichten. Ihre Lücken nähern sich im Zickzack als n . an erhöht und zeigt ein gerade-ungerades Verhalten. Die Strom-Spannungs-Kurven von ZZ- und KK-Nanobändern sind durch eine starke Einband-NDR- und Spin-Polarisation gekennzeichnet.

Abkürzungen

1D:

Eindimensional

2D:

Zweidimensional

A:

Sessel

CBM:

Leitungsband-Minimum

K:

Klein

VBM:

Valenzband-Maximum

Z:

Zickzack