Anisotrope Phasenumwandlung in einer kristallinen B2-CuZr-Legierung

Einführung

Metallische Massengläser (BMGs) haben aufgrund ihrer hervorragenden mechanischen und physikalischen Eigenschaften wie hohe Festigkeit, Elastizität, hohe Härte in Kombination mit ausgezeichneter Korrosionsbeständigkeit usw. große Aufmerksamkeit auf sich gezogen [1,2,3,4]. Dennoch versagen sie meist durch katastrophalen Sprödbruch durch lokalisierte Scherbänder [5, 6]. Dieser Mangel wurde in einigen CuZr-basierten Bulk-Metallic-Glas-Verbundwerkstoffen (BMGCs), die durch duktile B2-Phasen-CuZr-Partikel verstärkt wurden, bis zu einem gewissen Grad überwunden [3, 7,8,9,10,11]. Darüber hinaus würden einige kristalline B2-CuZr-Ausscheidungen von Natur aus durch die Kristallisation in CuZr-Glas unter Belastung gebildet werden und dann Zwillings- und Versetzungsgleiten durchlaufen, was die Änderung der mechanischen Eigenschaften von BMGs induziert, wie im Experiment festgestellt wurde [12]. Um BMGs mit B2-Phasen-CuZr-Ausscheidungen widerstandsfähiger zu machen und Hochleistungs-BMGs zu konstruieren, sollte zunächst das Verformungsverhalten von B2-Phasen-CuZr geklärt werden.

CuZr der B2-Phase ist eine Formgedächtnislegierung, die unter bestimmten thermomechanischen Bedingungen ihre ursprüngliche Form wiedererlangen kann [13, 14], was sich von den traditionellen kristallinen Materialien unterscheidet, die Versetzungsgleiten oder Zwillingsbildung als Hauptdeformationsmechanismus verwenden [15,16,17]. Die First-Principle-Rechnung basierend auf der Theorie der funktionalen Dichte kann verwendet werden, um den Adsorptionsprozess [18,19,20] und die Grenzflächeneigenschaft [21, 22] zu untersuchen, kann jedoch nicht angewendet werden, um die dynamische Entwicklung des Phasenübergangsverhaltens zu untersuchen zur Begrenzung des Berechnungsmaßstabs. Die Simulation der Molekulardynamik (MD) ist eine effektive Methode zur Untersuchung der mechanischen Eigenschaften und des Verformungsverhaltens von Materialien [23,24,25,26,27,28,29,30,31]. Sutrakar und Mahapatra untersuchten die Auswirkungen von Querschnittsabmessungen und Temperatur auf die Phasenumwandlung in Cu-Zr-Nanodrähten sowie die Zug-Druck-Asymmetrie durch MD-Simulation [32,33,34] und erhielten einige wertvolle Ergebnisse. Zum Beispiel wird die anfängliche B2-Phase durch die Keimbildung und Ausbreitung einer {100}-Zwillingsebene in eine körperzentrierte-tetragonale (BCT)-Phase umgewandelt. Amigoet al. verwendeten zwei Arten von Potentialen [35, 36] in ihren MD-Simulationen, um das Phasenumwandlungsverhalten zu untersuchen, und fanden heraus, dass das eine die martensitische Umwandlung von der B2- in die BCT-Struktur ergibt, das andere jedoch nicht [13].

Es ist bekannt, dass die Anisotropie von Kristallen eine wichtige Rolle bei der Verformung von Materialien spielt. Verschiedene Verformungsmechanismen können bei der Verformung eine dominante Rolle spielen, wenn die Last entlang unterschiedlicher Kristallorientierungen aufgebracht wird [37]. Perfektes Versetzungsgleiten und Zwillingsbildung sind beispielsweise die Hauptdeformationsmechanismen für die Nanoindentation auf (001)- und (111)-Oberflächen von Vanadiumnitrid (VN) mit einem zylindrischen Indenter [38, 39], die eine offensichtliche anisotrope Plastizität zeigen. Bei BCC-Eisen-Nanodrähten zeigt die Phasenumwandlung eine komplizierte Abhängigkeit von der kristallographischen Orientierung, entlang derer die Last aufgebracht wird, <001>-orientierter Draht zeigt eine BCC→FCC-Umwandlung, aber <011> und <111>-orientierter Draht folgt einem BCC→ HCP-Transformation [40]. Das Atomverteilungsarray in der B2-Struktur ist analog zu dem in einer BCC-Struktur, aber es gibt zwei Arten von Elementen in der B2-Struktur. Die Kristallorientierung der Verstärkungspartikel in BMGs ist normalerweise gestreut, daher sollte die Belastungsrichtung unterschiedliche Einflüsse auf die Zähigkeitswirkung verschiedener Partikel haben. Daher ist es notwendig, das Deformationsverhalten der Verstärkungspartikel bei Belastung entlang verschiedener Orientierungen zu untersuchen.

Uniaxialer Zug und Druck, als zwei grundlegende Belastungsmodi, die normalerweise verwendet werden, um die grundlegenden mechanischen Eigenschaften von Materialien zu bewerten. In dieser Arbeit wird eine Reihe von MD-Simulationen von einachsigen Zug- und Druckversuchen von kristallinem B2-CuZr entlang der Orientierungen [001], [110] und [111] durchgeführt, um die Abhängigkeit der Phasenumwandlung von der Belastungsorientierung sowie von Zug und Druck zu untersuchen (T/C) Asymmetrie.

Methoden

Die bekannte Embedded-Atom-Methode (EAM) [41] wurde ausgewählt, um die interatomare Kraft des Cu-Zr-Systems zu beschreiben. Das EAM-Potenzial wird häufig verwendet, um das mechanische Verhalten von Metallen und ihren Legierungen zu untersuchen [42,43,44,45,46]. Basierend auf dem EAM-Framework haben Mendelev und seine Kollegen in den Jahren 2007 [35], 2009 [36] und 2016 [47] dreimal die potenziellen Parameter identifiziert und optimiert. In dieser Arbeit werden die Parameter der neuesten Version des interatomaren Potentials für Cu-Zr [47] aus dem Jahr 2016 verwendet. Diese Parameter können eine realistischere stabile und instabile Stapelfehlerenergie im Vergleich zu der 2009 entwickelten [36] ergeben und können die Eigenschaften von kristallinem CuZr besser beschreiben.

Drei Proben mit der Belastungsachse z entlang der [001], [110] bzw. [111] vorbereitet werden, wie in 1 gezeigt. Vor dem Laden wird ein konjugierter Gradienten-(CG)-Algorithmus verwendet, um die Energie des Systems zu minimieren, um einen optimierten stabilen Aufbau. Mechanische Tests werden bei 300 K Raumtemperatur simuliert. Anschließend wird das System mit dem isotherm-isobaren NPT-Ensemble bei T . entspannt =300 K für 20 ps, ​​um einen Gleichgewichtszustand mit druckfreiem Zustand zu erreichen. Es hat sich herausgestellt, dass der Dehnungsrateneffekt des nano-polykristallinen Materials unbedeutend wird, wenn die Dehnungsrate im Bereich zwischen 5 × 10 ⁸ . variiert und 1 × 10 ⁹ s ⁻¹ , daher wird der Dehnungsrate 1 × 10 ⁹ . zugewiesen s ⁻¹ indem sowohl die Genauigkeit als auch die Berechnungseffizienz umfassend berücksichtigt werden [48, 49]. Daher wird jedes Sample im z gestreckt/komprimiert -Richtung bei einer Dehnungsrate von 10 ⁹ s ⁻¹ beim Laden; inzwischen wird das NPT-Ensemble mit Nose/Hoover-Barostat eingesetzt [50] um den Druck in x . frei zu halten - und y -Richtungen. In der Relaxations- und der Belastungsphase werden periodische Randbedingungen in x . angewendet -, y -, und z -Wegbeschreibung.

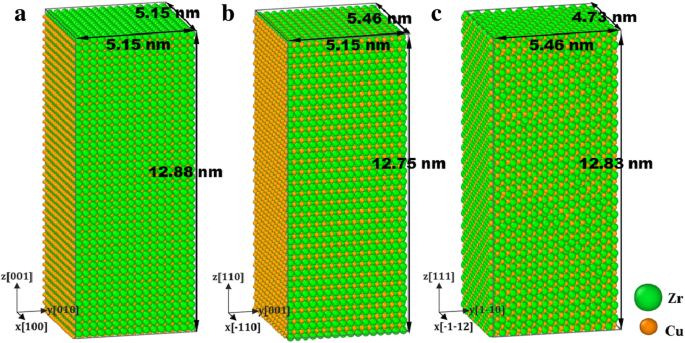
Proben mit axialem z entlang a [001], b [110] und c [111], eingefärbt mit Atomtyp

Die Common Neighbor Analysis (CNA) [51], ein Algorithmus zur Charakterisierung der lokalen strukturellen Umgebung, wird normalerweise als effektive Methode zur Klassifizierung der Atome in einem kristallinen System verwendet. Der zweitnächste Nachbarabstand in einer BCC-Struktur ist nur 15% größer als der nächste; daher würde das CNA-Verfahren bei starken thermischen Schwankungen und Belastungen an Zuverlässigkeit verlieren. Um diesen Mangel zu überwinden, wurde die Methode des polyedrischen Template-Matching (PTM) vorgeschlagen, um die lokale strukturelle Umgebung von Partikeln zu klassifizieren und die lokale kristalline Struktur einfacher kondensierter Phasen (FCC, BCC, HCP usw.) zu identifizieren [52]. Im Vergleich zur CNA [51] verspricht die PTM-Methode eine höhere Zuverlässigkeit bei starken thermischen Schwankungen und Belastungen [52]. B2- und BCC-Strukturen haben eine analoge Atomanordnung; daher ist die durch dieses Verfahren identifizierte BCC-Struktur tatsächlich die B2-Struktur. Nach der lokalen Mikrostrukturanalyse für die durch MD-Simulation mit PTM gewonnenen Daten werden die Atome nach folgenden Regeln eingefärbt:blau für BCC (B2)-Struktur, grün für FCC-Struktur, rot für Stapelfehler oder HCP-Struktur, lila für einfache kubische (SC) und weiß für Korngrenzen oder Versetzungskerne. Es sollte beachtet werden, dass einlagige, doppellagige und kontinuierliche mehrlagige rote Atome als Zwillingsgrenze, Stapelfehler bzw. HCP-Struktur dargestellt werden. Lokale Regionen mit roten, grünen, blauen und weißen Atomen sind amorph.

Als ergänzende Methode der Mikrostrukturanalyse wird der Zentrosymmetrieparameter (CSP) verwendet, um die lokale Unordnung zu beschreiben [53]. Für jedes Atom wird der CSP mit der fließenden Formel berechnet:

wobei N = 12 oder 8 ist die Zahl der ersten nächsten Nachbarn eines Zentralatoms in der FCC- oder B2-Struktur und R _ich und R _i+N/2 sind die Vektoren vom Zentralatom zu einem bestimmten Paar der nächsten Nachbarn. Der CSP ist null für ein Atom, dessen nächste Nachbarn sich an ihren perfekten Gitterplätzen befinden. Wenn ein Defekt wie eine Leerstelle oder eine Versetzung in der Nähe eines Atoms vorliegt, wird der CSP des Atoms viel größer als der durch lokale Atomschwingungen verursachte. Zur Darstellung atomarer Konfigurationen wird die offene Software Ovito von Stukowski [54] verwendet.

Ergebnisse und Diskussionen

Stress-Dehnungs-Kurven

Abbildung 2 zeigt die Spannungs-Dehnung (σ -ε ) Kurven für CuZr der B2-Phase, das einer einachsigen Zug- und Druckbelastung ausgesetzt ist, entlang [001], [110] und [111]. Es kann festgestellt werden, dass die Spannung größer ist als die im Experiment [55], weil (1) die bei der MD-Simulation verwendete Zeitskala sich von der im Experiment verwendeten unterscheidet, was zu einer viel höheren Eindrückgeschwindigkeit als im Experiment führt; und (2) die Fehler einschließlich Punktfehler, Versetzungen und Korngrenzen usw. werden in den Simulationen nicht berücksichtigt. Im Anfangsstadium entwickeln sich diese Kurven linear und zeigen dann unterschiedliche Trends. Nach dem ersten Peak lassen sich diese Kurven in drei Gruppen einteilen. In Gruppe I fallen die Kurven schnell auf niedrige Spannungsniveaus ab, wie z. B. Kompression entlang [110] und [111]. In Gruppe II fallen die Spannungen auf eine Plattform und schwanken mit der Zunahme der Dehnung nach dem ersten Spitzenwert, wie z. B. Zug entlang [001], [110] und Druck entlang [001]. Die Kurven steigen dann zu ihren zweiten Gipfeln an, bevor sie schließlich scharf abfallen. In Gruppe III fällt die Kurve schnell auf niedrige Belastungsniveaus ab und schwankt dann in einem Zickzackmuster, wie z. B. Spannung entlang [111]. Vor dem ersten Peak verbleiben die Proben in der B2-Struktur und es kann kein offensichtliches Versetzungsgleiten und keine Zwillingsbildung beobachtet werden, was als elastische Verformung angesehen werden kann. Im linear-elastischen Stadium ist der Elastizitätsmodul E kann durch Anpassen der Steigung jeder Kurve im Bereich von 0,00 <ε . erhalten werden <0,02, und in Tabelle 1 aufgeführt, wo ersichtlich ist, dass die [001]-Orientierung die weichste und [111] die steifste ist. Dies stimmt mit den Ergebnissen von Bulk-BCC-Eisen überein [40]. Das E der Probe unter Druck ist mit Ausnahme der [001]-Orientierung größer als die unter Spannung, in Übereinstimmung mit der bei Cu-Einkristallen [56] beobachteten, die der höheren Reibung unter Druck zugeschrieben werden sollte [56]. Die übrigen Kurven im elastischen Stadium unter Druck weichen offensichtlich von denen unter Zug ab, was auf die asymmetrische Zug- und Drucknatur des interatomaren Potentials zurückzuführen ist [57]. Nach dem ersten Peak ist unklar, ob die Verformung auf Versetzungsschlupf oder Phasenumwandlung zurückzuführen ist; daher kann diese Region nicht als inelastische oder plastische T/C-Asymmetrie angesehen werden, die sich von Arbeiten anderer unterscheidet [57,58,59]. Im Fließteil werden die Deformationsmechanismen der Probe, die Belastungen in verschiedenen Richtungen ausgesetzt sind, im Detail diskutiert.

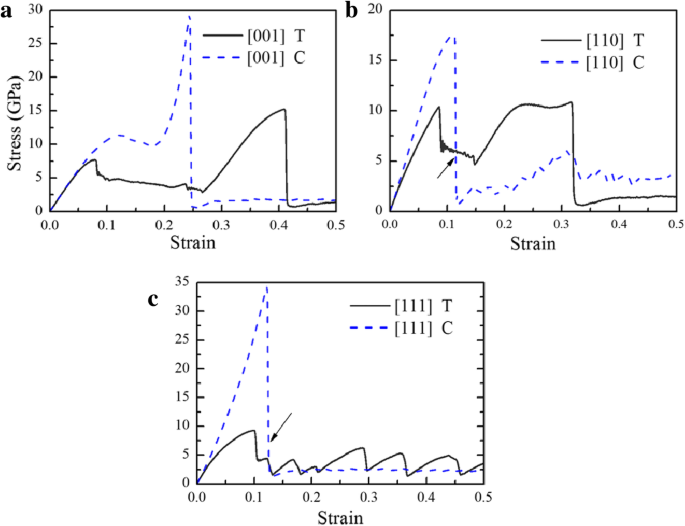
σ -ε Kurven von Proben unter Zug (T) und Druck (C). a [001], b [110] und c [111]

Fehlerverhalten

Abbildung 3 zeigt die atomaren Strukturen und die radialen Verteilungsfunktionen (RDFs) der Proben unter Kompression entlang [110] und [111], deren σ -ε Kurven sind in Abb. 2 zu sehen, die als [110] C und [111] C bezeichnet sind. Abbildung 3a, d zeigt die Anfangsproben [110] und [111] nach Relaxation bei 300 K, wobei zu sehen ist, dass die Atome in der B2-Struktur. Wenn ε auf 0.115 bzw. 0.125 für [110] C bzw. [111] C erhöht wird, erscheint der Bereich mit gemischten Strukturen, wie in Abb. 3b, f. Das Gefüge im Mischbereich wird als Mischphase bezeichnet. Die Nukleation der Mischphase entspricht der Phase der schnellen Tropfen der Kurven [110] C und [111] C in Abb. 2b, c, die mit Pfeilen markiert ist. Daher verursacht die Umwandlung der lokalen Struktur von B2 in eine gemischte Phase den schnellen Spannungsabfall. In der Fließphase ist die Variation des Volumenanteils der Mischphase der Hauptmechanismus, um weitere Verformungen aufzunehmen, die lokalen Strukturen in den Proben unter Kompression entlang [110] und [111] bei ε =0,25 sind in Abb. 3c bzw. g dargestellt. Um die Struktur in der gemischten Region zu spezifizieren, wird die radiale Verteilungsfunktion (RDFs ), g (r ), der Proben unter Kompression entlang [110] und [111] bei verschiedenen Dehnungen sind in Abb. 3d, h gezeigt. Die Gipfel des g (r ) der Proben bei ε =0 und ε =0,25 sind scharf, was darauf hinweist, dass sie immer noch das kristalline Merkmal beibehalten. Während die Gipfel des g (r ) für die gemischten Regionen, d. h. die Probe ohne B2-Regionen, sind mit Ausnahme der ersten stumpf, was darauf hinweist, dass sich die gemischte Region in einem amorphen Zustand befindet. Der Versetzungsextraktionsalgorithmus (DXA) [60] wird auch verwendet, um zu erkennen, ob eine Versetzungsnukleation vorliegt und keine offensichtlichen Versetzungen während des gesamten Verformungsprozesses zu finden. Daher wird die Amorphisierung der B2-Phase als Hauptfehlermodus durchgeführt, was zu einem schnellen Abfall führt, der in Abb. 2b, c mit Pfeilen markiert ist.

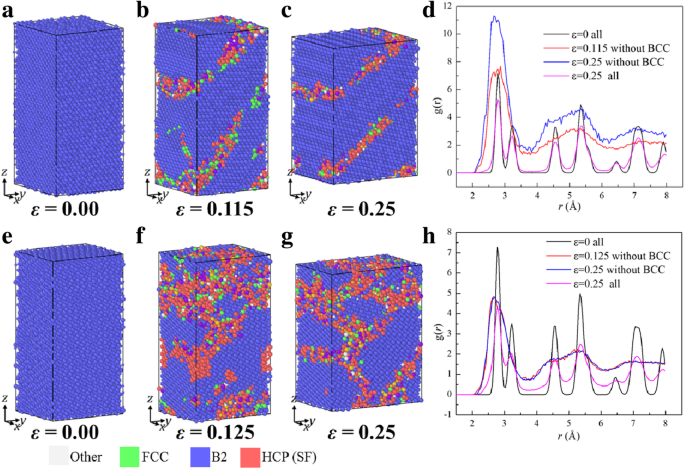
Atomare Konfigurationen und RDFs von Samples unter Kompression. a –d Entlang [110] und e –h entlang [111]

Abbildung 4 zeigt die atomaren Konfigurationen nach der schnellen Falldehnung (Versagensdehnung) der Proben unter Zug entlang [001], [110] und Kompression entlang [001], deren σ -ε Kurven gehören zur Gruppe II. In Abb. 4 ist zu sehen, dass sich gemischte Bereiche bilden, ähnlich denen in Gruppe I, was darauf hinweist, dass Amorphisierung auch der Hauptfehlermodus ist (Abb. 4). Diese gemischten Bereiche sind jedoch von grünen und roten Atomen umgeben (FCC- und HCP-Struktur), was sich von der B2-Struktur in Fig. 3 unterscheidet. Dieser Unterschied zeigt, dass die gemischte Phase von der B2-Struktur unter Kompression in Fig. 3 umgewandelt wird, aber von FCC für Probe [001] unter Zug und Druck und von HCP für Probe [110] unter Zug.

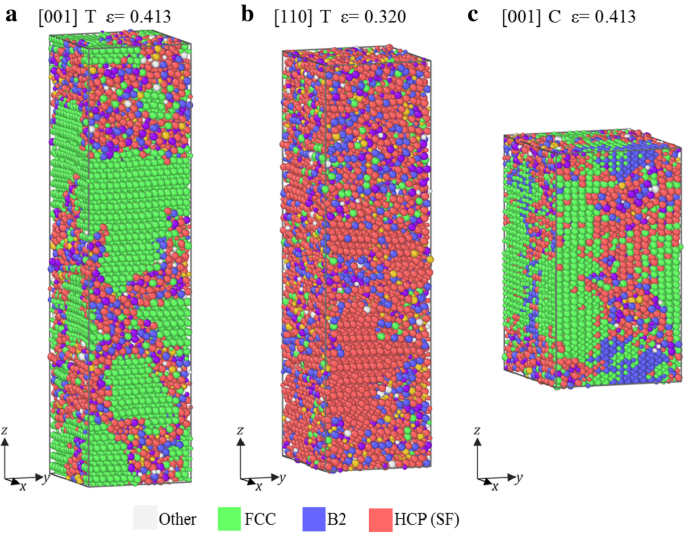
Atomare Konfigurationen in Proben bei Bruchdehnung. a Unter Spannung entlang [001], b unter Spannung entlang [110] und c unter Kompression entlang [111]

Phasentransformationen

Abbildung 5 zeigt die σ -ε Kurve der Probe [001] unter Spannung, wobei auch die Mikrostrukturen an typischen Punkten (gekennzeichnet mit A, B, ..., G) gezeigt werden. Die Atome am Punkt A (ε =0,079) sind in der B2-Struktur, was darauf hinweist, dass vor ε =0,079 ist die Verformung in der Probe elastisch. Es findet jedoch eine lokale Transformation von B2 zu FCC statt, wie im Einschub von ε . gezeigt =0,082 in Abb. 5, was zum ersten schnellen Abfall (A→B) auf ε . führt =0,082, wobei die Freisetzung der elastischen Energie, die aufgrund der Umverteilung der atomaren Konfiguration gespeichert ist, die Energie für die Phasenumwandlung liefert. Im Fließstadium von B→F wird die gespeicherte elastische Energie mit fortschreitender Phasenumwandlung weiter freigesetzt, was zu einer Reduzierung der Spannung führt. Die lokale Struktur der Probe wird bei ε . vollständig FCC =0,242 (Punkt E). Und die Struktur ändert sich zwischen Punkt E und F, aber die Spannung sinkt mit zunehmender Belastung. Um die Änderung der Mikrostruktur aufzuzeigen, ist die Verteilung von g (r ) und die Variation der Atomzahl (N ) gegen CSP (N -CSP ) der Probe bei ε =0,242, 0,254 und 0,267 (zwischen den Punkten E und F) werden berechnet und in Abb. 6a bzw. b gezeigt, wobei die Höhe jedes Peaks mit der Zunahme der Dehnung zunimmt, was darauf hindeutet, dass das System kompakter wird.

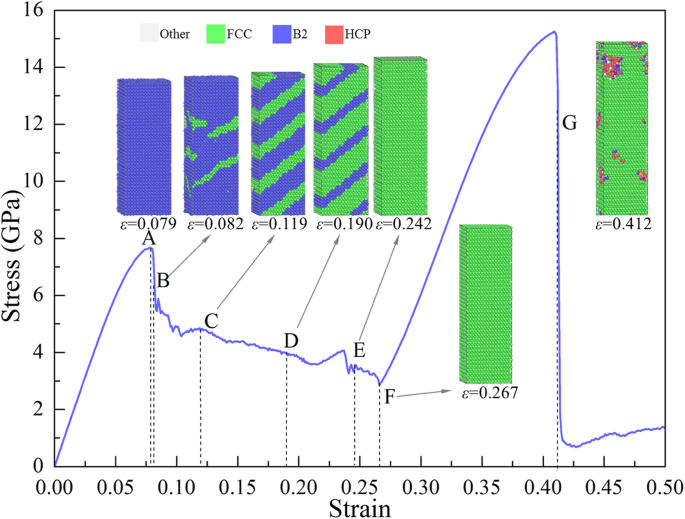
σ-ε Kurve der Probe unter Spannung entlang [001], gefärbt mit lokaler Struktur, wobei Blau, Grün und Rot B2, FCC bzw. amorphe Phasen darstellen

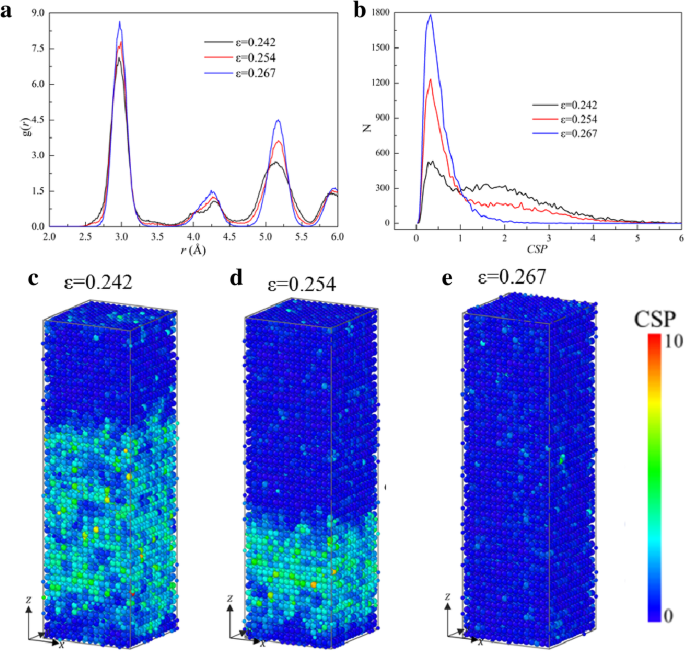
a RDF , b N -CSP Plots der Probe unter Spannung entlang [001]. c –e Verteilung von CSP in Probe bei verschiedenen Belastungen

Um zu charakterisieren, ob ein Atom Teil eines perfekten Gitters oder eines lokalen Defekts ist, z [53] der Atome mit der Anzahl der nächsten Nachbarn der FCC-Struktur (N =12) berechnet, wie in Abb. 6c–e gezeigt. Und ein größerer CSP bedeutet eine größere Abweichung vom perfekten Gitter [17]. In Abb. 6b ist zu sehen, dass die Zahl der Atome mit CSP < 1 mit zunehmender Dehnung zunimmt, was auch an der Verteilung der CSPs der Atome in Abb. 6c–e intuitiver zu erkennen ist. Es unterscheidet sich von den üblichen Ergebnissen, dass das CSP normalerweise mit der Zunahme der Belastung nicht abnimmt. Daher sollte das Hauptverformungsverhalten in dieser Stufe auch der Phasenumwandlung von imperfekter FCC zu perfekter FCC zugeschrieben werden. In der Fließphase wird die Probe mit FCC-Strukturen gedehnt und die Spannung nimmt bis zum Erreichen der zweiten Fließgrenze zu. Dann fällt die Kurve steil ab, was eher einer lokalen Amorphisierung als einer Versetzungs- oder Gleitkeimbildung entspricht.

Zur Veranschaulichung der Phasenumwandlung des Materials während der Verformung zeigt Abb. 7 einige yoz Scheiben der Probe [001] unter Spannung bei unterschiedlichen Dehnungen. Die horizontalen und vertikalen gestrichelten Linien werden als Referenzen verwendet, um zu erkennen, ob sich die atomaren Strukturen drehen und abweichen. Mit der Zunahme von ε von 0,0 bis 0,079 liegen die Atome auf Linien parallel zur horizontalen und vertikalen Achse, was darauf hinweist, dass sie die lokale B2-Struktur aufweisen. Das Atomarray in Abb. 7b ändert sich jedoch zu dem in Abb. 7c als ε von 0,079 bis 0,119, wenn sich einige B2-Strukturen in die FCC-Struktur umwandeln. Der Winkel zwischen den Arrays ändert sich von 90° in Fig. 7b für die B2-Struktur auf ~ 85° in Fig. 7c für die FCC-Struktur, wobei die Gitterorientierung von der vertikalen Achse um 5° im Uhrzeigersinn abweicht, aber die atomare Anordnung der B2-Struktur tut dies nicht ändern sich offensichtlich und hat keine offensichtliche Rotation. Während 0,119 <ε < 0,190, die FCC-Fläche nimmt zu und die Anordnung der grünen Atome dreht sich allmählich gegen den Uhrzeigersinn. Bei ε =0,242, die gesamte B2-Struktur wandelt sich in FCC-Strukturen um, wie in Fig. 7e gezeigt, wo die drei Gitterorientierungen jeweils fast parallel zu den drei Achsen werden, aber es gibt immer noch eine deutliche Abweichung, was anzeigt, dass die FCC-Struktur nicht perfekt ist, was ist in Übereinstimmung mit dem in Fig. 6c gezeigten. Im Fließzustand tendiert die Atomanordnung regelmäßig, wie in Abb. 7f bei ε . gezeigt =0,267, was als {110}-Ebene der FCC-Struktur erkannt wird, wobei ihre Kristallorientierung in horizontaler und vertikaler Richtung von [010] und [001] der B2-Struktur zu <110> und <001> der FCC-Struktur geändert wurde.

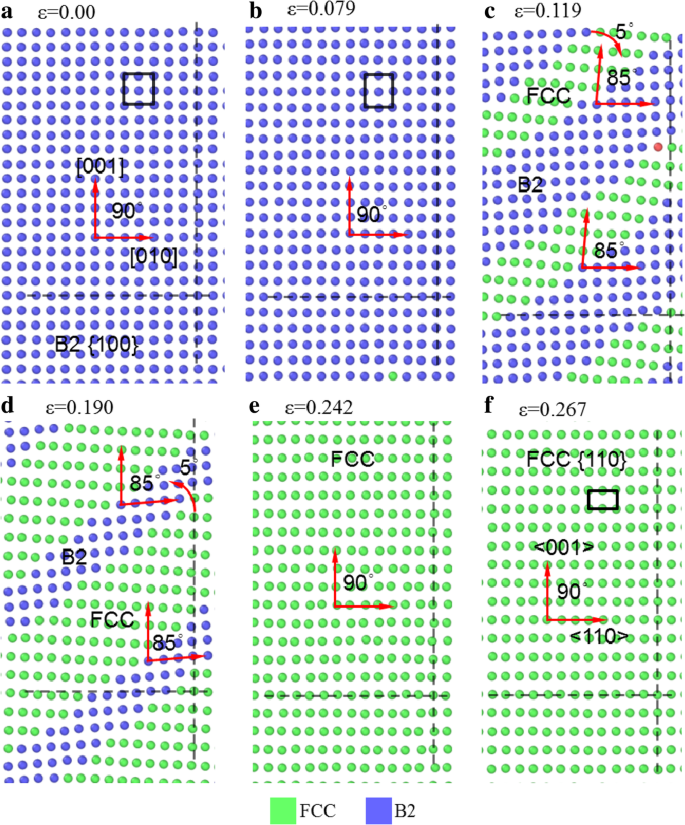
yoz Scheiben der [001]-Probe unter Spannung bei unterschiedlichen Dehnungen, gefärbt mit einer lokalen Gitterstruktur, wobei Blau, Grün und Rot B2, FCC bzw. amorphe Phasen darstellen

Die Simulation für das Verhalten der Probe (100) beim Entladen von verschiedenen maximalen Zugdehnungen (ε _max =0,1, 0,2 bzw. 0,3) werden ausgeführt und die σ -ε Kurven sind in Abb. 8 dargestellt. Es ist zu erkennen, dass die Entlastung σ -ε Kurven zwischen ε =0,266 und ε =0,056 überlappen die Belastungskurve nicht, können aber das elastische σ . treffen -ε Kurve bei ε =0,056 und dann zurück zum Ursprung entlang des elastischen σ -ε Kurve, die die superelastische Charakteristik zeigt. Die Lade- und Entladepfade bilden Hystereseschleifen, die auf die unterschiedlichen Pfade der Vorwärts- und inversen Phasentransformationen zurückzuführen sind.

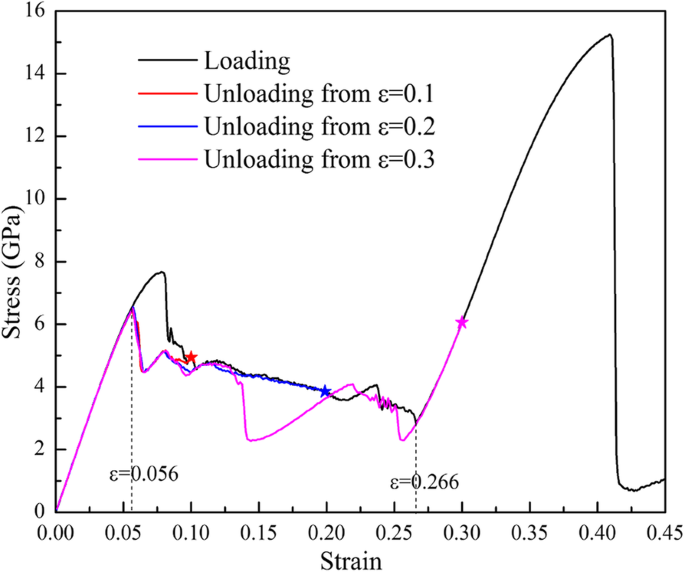
Be- und Entladen σ -ε krümmt Spannung entlang [001] von verschiedenen Dehnungen

Die σ -ε Die Kurve der Probe [001] unter Kompression weist einen ähnlichen Trend auf, wie in 9a gezeigt, der in vier Stufen unterteilt werden kann:(1) σ steigt linear mit der Zunahme der Dehnung an; (2) σ fällt auf ein Plateau; (3) σ steigt mit zunehmender Dehnung linear mit einer größeren Steigung zum zweiten Peak an; (4) σ fällt steil auf das zweite Plateau ab. Durch Analysieren der lokalen Strukturen mit PTM kann man feststellen, dass die meisten Atome als B2-Struktur identifiziert werden, bevor sie den zweiten Peak erreichen, mit Ausnahme einiger verstreuter Atome, die als andere lokale Strukturen identifiziert werden, wie in 9a gezeigt. Nach bisherigem Verständnis ist jedoch eine plötzliche Änderung der σ -ε Kurven entspricht normalerweise der Änderung der Mikrostruktur. Um es weiter zu bestätigen, das N -CSP Diagramme werden berechnet und in Abb. 9b gezeigt, in denen der CSP für jedes Atom bei verschiedenen Dehnungen mit den nächsten Nachbarn der B2-Struktur berechnet wird (N =8). Wenn ε =0, der CSP der Atome ist aufgrund des Temperatureinflusses größer als 0, aber kleiner als 1, was bedeutet, dass die Atome in perfekter B2-Struktur vorliegen. Mit der Zunahme von ε , lassen sich die Atome nach ihren CSPs in zwei Gruppen einteilen:CSP < 1 und 5 ε < 0.121, die CSPs an den zweiten Peaks sind gleich, aber die Anzahl der Atome in diesem CSP Die Reichweite nimmt zu und ist tendenziell stabil, was auf die Bildung neuer Phasen oder Defekte (wie Stapelfehler) hinweist. Der CSP beim zweiten Peak nimmt mit dem weiteren Anstieg von ε . ab , d. h. die zweite Welle bewegt sich nach links. Abbildung 10 zeigt die Entwicklung der Bindungslänge in einer Elementarzelle bei verschiedenen Belastungen. Bei ε =0, acht Cu-Atome an den Ecken und ein Zr-Atom im Körperzentrum bilden die B2-Struktur. Die Beziehung zwischen den Gitterparametern ist a =b =c . Mit der Zunahme von ε , die Länge der Bindung in xoy Ebene zunimmt, aber das in xoz Ebene abnimmt. Durch Berechnung der Dehnung in den anderen beiden Richtungen während der Belastung kann man feststellen, dass die Dehnungen in den anderen beiden Richtungen vor dem zweiten Peak identisch sind. Daher sind die Längen der Bindungen entlang x- und y -Richtungen sollten identisch sein und größer als die entlang der z -Richtung. Die Beziehung zwischen Gitterparametern wird zu a =b> c . Diese Anordnungen von Atomen können als BCT-Struktur erkannt werden. Zusammenfassend lässt sich sagen, dass die Transformation von einer B2-Struktur zu einer BCT-Struktur der Hauptdeformationsmechanismus für Probe [001] unter Kompression ist.

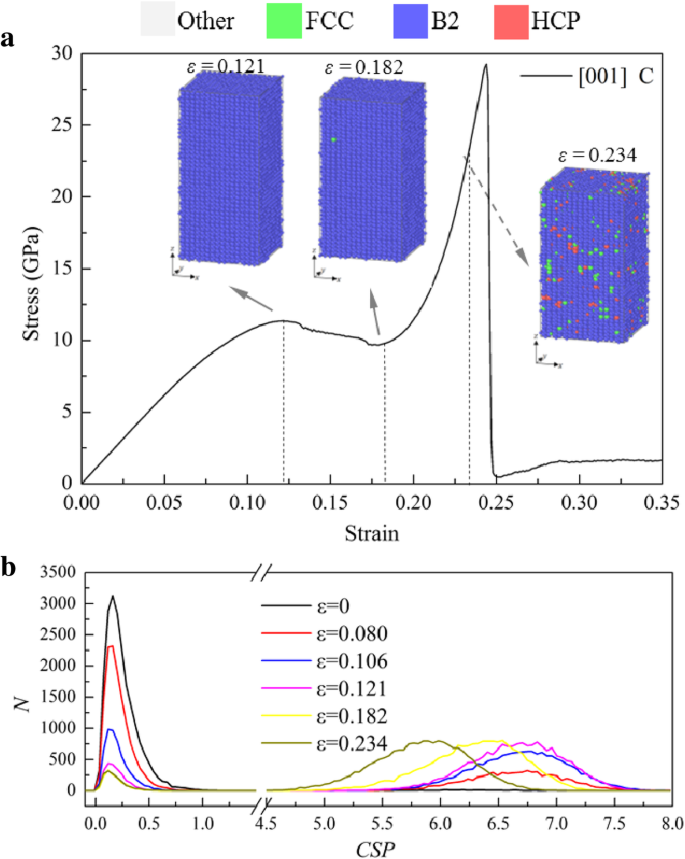
Antworten der Probe [001] unter Kompression. a σ-ε Kurve und typische Atomkonfigurationen, mit Atomen, die mit lokalen Strukturen gefärbt sind, die durch PTM identifiziert wurden. b N -CSP Grundstücke

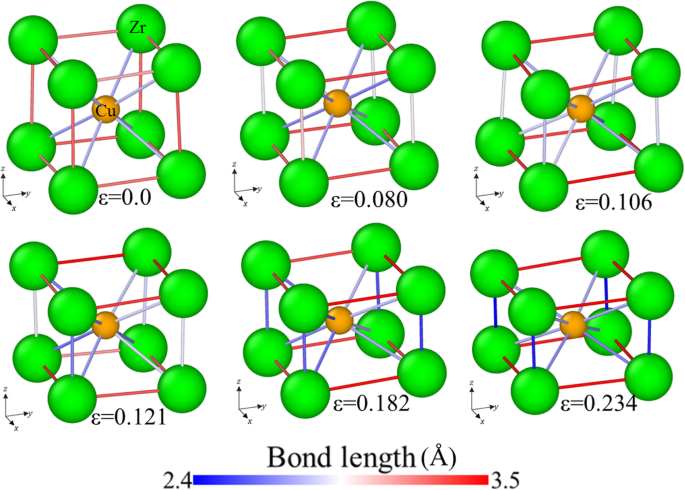
Entwicklung der Bindungslänge für die Probe [001] unter Druck, mit Bindungen, die mit ihrer Länge gefärbt sind

Abbildung 11a zeigt die Reaktion der Probe [110] unter Spannung. Der erste Peak (Punkt A) entspricht der Fließgrenze der B2-Struktur, dann wandelt sich eine lokale B2-Struktur in die HCP-Struktur um, was zu einem starken Abfall führt. Mit der Zunahme von ε , nimmt die Spannung bis zum Punkt C ab, wenn die Probe vollständig in HCP umgewandelt wird. Abbildung 11b, c ist der xoy einschichtige Scheiben bei ε =0 bzw. 0.150, wobei zu erkennen ist, dass sich die Cu- und Zr-Atome im Anfangsstadium in einer identischen Atomschicht befinden (Abb. 11b). Cu- und Zr-Atome werden jedoch bei ε . in benachbarte Schichten getrennt =0,150 (Abb. 11c), was zur Phasenumwandlung von B2 zu HCP führt. Dann mit der Zunahme von ε , σ steigt mit einer geringeren Steigung als in der anfänglichen linearen Phase bis zum Punkt D an, gefolgt von einem scharfen Abfall auf ein niedriges Spannungsniveau, entsprechend einem Versagen aufgrund lokaler Amorphisierung.

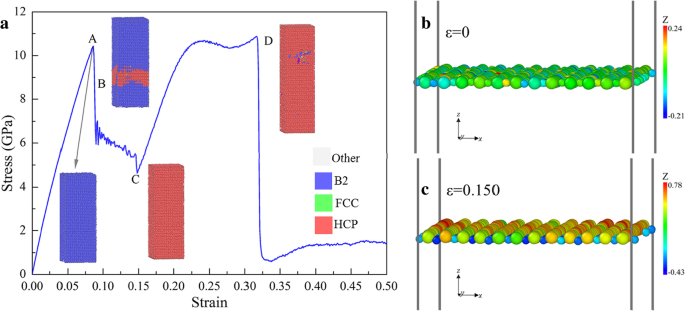
a Verformungsverhalten der Spannung längs [110], eingefärbt mit PTM. b , c Atomscheiben auf xoy Ebene bei ε =0 bzw. 0,150

Schlussfolgerungen

In dieser Arbeit werden die Reaktionen und Phasenumwandlungen von CuZr-Proben, die uniaxialen Zug- und Druckbelastungen entlang der Orientierungen [001], [110], [111] ausgesetzt sind, mit Hilfe von Molekulardynamiksimulationen untersucht, wobei das neueste interatomare Potential genutzt wird, aus dem die folgende Hauptschlussfolgerungen können gezogen werden:

1. 1.

   Die mechanischen Reaktionen der CuZr-Proben unter Zug und Druck zeigen eine offensichtliche Asymmetrie, und ihr Hauptversagensmechanismus sollte die lokale Amorphisierung sein.

2. 2.

   Es gibt drei Arten von Phasentransformationen:B2→FCC, B2→BCT und B2→HCP in Zug und Druck entlang [001] und Zug entlang [110].

3. 3.

   Die Phasenumwandlungen B2→FCC, B2→BCT und B2→HCP werden durch jeweils einzigartige Mechanismen realisiert, die Gitterrotation (~ 5°), gleichmäßige Verformung und Trennung von der Cu- und Zr-Atomschicht für jeden sind.

4. 4.

   Der Phasenumwandlungsbereich kann nach dem Entladen vor der lokalen Amorphisierung wiederhergestellt werden, was die Superelastizität zeigt.

Die Ergebnisse sind wichtig für die Erforschung der mechanischen Eigenschaften und Deformationsmechanismen von nanokristallinem CuZr und für die Anwendung nanokristalliner CuZr-Partikel als Verbesserungsmittel zur Verbesserung der Zähigkeit von metallischem Glas.

Verfügbarkeit von Daten und Materialien

Die in der aktuellen Studie verwendeten bzw. analysierten Datensätze sind auf begründete Anfrage beim entsprechenden Autor erhältlich.

Abkürzungen

BCC:

Körperzentrierter Kubikraum

BCT:

Körperzentriert-tetragonal

BMG:

Bulk-Metallic-Brille

BMGC:

Metallische Glasverbundwerkstoffe in Massen

CG:

Farbverlauf konjugieren

CNA:

Gemeinsame Nachbaranalyse

CSP:

Zentrosymmetrieparameter

Ku:

Kupfer

CuZr:

Kupfer-Zirkonium

DXA:

Algorithmus zur Extraktion von Versetzungen

EAM:

Methode mit eingebetteten Atomen

FCC:

Kubisch flächenzentriert

HCP:

Sechseckig dicht gepackt

MD:

Molekulardynamik

NPT:

Konstante Partikelanzahl, Druck und Temperatur

PTM:

Abgleich von polyedrischen Vorlagen

RDF:

Radiale Verteilungsfunktion

AGB:

Spannung und Kompression

VN:

Vanadiumnitrid

Zr:

Zirkonium

ε :

Stamm

σ :

Stress