atomare Charakterisierung der Schlupfverformung und nanometrische Bearbeitbarkeit von einkristallinem 6H-SiC

Einführung

Als Halbleitermaterial der dritten Generation mit großer Bandlücke hat SiC die Eigenschaften eines hohen Durchbruchfeldes, einer hohen Strahlungstoleranz, einer hohen Ladungsträgersättigungsgeschwindigkeit, einer schnellen Wärmeleitfähigkeit, einer kleinen Dielektrizitätskonstante und einer konstanten chemischen Eigenschaft, so dass es in den Bereichen breite Anwendung findet von optoelektronischen Hochtemperatur-, Hochfrequenz-, Hochleistungs-, Anti-Strahlungs- und Kurzwellenlängen-Bauelementen und optoelektronischer Integration [1].

Die am häufigsten verwendeten Kristalle von SiC sind 3C, 4H und 6H. Bearbeitungsverfahren wie Schleifen/Läppen/Polieren sind nach wie vor die Hauptverfahren bei der Bearbeitung von einkristallinem SiC. Allerdings liegt das Härteverhältnis zwischen Diamant und SiC nahe 2:1 (die Bearbeitungstiefe < 50 nm)), was deutlich unter dem empfohlenen Wert von 5:1 für den Zerspanungsprozess liegt [2]. Starker Verschleiß des Schneidwerkzeugs und Beschädigungen unter der Oberfläche wirken sich direkt auf die Qualität des Wafers aus. Um diese Probleme anzugehen, wurde viel Arbeit geleistet, um das Entfernungsverhalten von SiC auf der Nanoskala zu verstehen. Der Abtragsmechanismus von 3C-SiC und die Beeinflussung der Bearbeitungsfaktoren wurden gründlich untersucht, wie der plastische Verformungsmechanismus beim Zerspanen [3,4,5,6,7], Werkzeugverschleiß [8], Reibungsverhalten [9 ] und Anisotropie von 3C-SiC [10] und Einfluss der Schnitttemperaturen [11].

6H-SiC hat eine komplexere ABCACB-Stapelstruktur. Obwohl der Abtragsmechanismus von 6H-SiC bei der SPDT-Bearbeitung (Single Point Diamond Turning) (wie der Einfluss des Werkzeugspanwinkels auf den Abtragsprozess [12] und der Spröd-Duktil-Übergang [13]) untersucht wird, ist die Forschung offensichtlich weniger als 3C-SiC. Die Bandlücke von 6H-SiC (3 eV) ist offensichtlich höher als die von 3C-SiC (2,3 eV). Gegenwärtig ist das technologische Niveau des 6H-SiC-Stabwachstumsprozesses viel höher als das von 3C-SiC. 6H-SiC wird in industriellen Anwendungen weitaus häufiger verwendet als 3C-SiC. Entsprechende Bauelemente wurden in Hochfrequenz-, Hochleistungs- und Hochtemperaturfeldern eingesetzt, wie beispielsweise Schottky-Gleichrichter, Thyratron und Leistungs-MOSFET (Metall-Oxid-Halbleiter-Feldeffekttransistor). Um die Qualität der bearbeiteten Oberfläche/Untergrund von 6H-SiC zu verbessern, besteht derzeit das effizienteste und effektivste Mittel darin, eine geeignete Kombination aus Kristallebene (Bearbeitungsoberfläche)/Kristallorientierung (Bearbeitungsrichtung) zu finden, die für den Prozess von 6H . besser geeignet ist -SiC.

Scratch-Experimente und Simulationen sind einige der gebräuchlichsten und effektivsten Methoden, um das Abtragsverhalten zu untersuchen [14, 15]. Die Erforschung des Materialabtragsmechanismus beim Ritzprozess hat eine große richtungsweisende Bedeutung für den eigentlichen abrasiven Bearbeitungsprozess. Die Molekulardynamikmethode kann einen Prozess der Schadensbildung und -beseitigung im Nanomaßstab bereitstellen. Daher wurde die molekulardynamische Ritzsimulation verwendet, um das Abtragsverhalten von 6H-SiC unter dem Einfluss der Kristallographie-induzierten Anisotropie zu analysieren.

Methode

Die Schnittsimulationen in diesem Artikel wurden mit einem großskaligen atomaren/molekularen massiv parallelen Simulator (LAMMPS) [16] durchgeführt. OIVTO [17] und die Methode zur Identifizierung der Diamantstruktur [18] wurden in dieser Studie zur Modellvisualisierung und Defektidentifikation verwendet. Die Implementierungen der Werkstück- und Werkzeugmodellierung waren auf LAMMPS ohne Zuhilfenahme anderer Software angewiesen. Wie in Abb. 1a–c dargestellt, wurden sowohl das Werkstück als auch das Werkzeug als verformbare Körper eingestellt und das Verschleißverhalten während der Simulation untersucht. Das Werkzeug- und Werkstückmodell wurde in drei Teile unterteilt:eine atomare Grenzschicht, eine thermostatische Atomschicht und eine Newtonsche Atomzone. Um das Werkstück in der Ausgangsposition zu halten, wurden die Grenzschichtatome am unteren und rechten Ende des Werkstücks fixiert. Atome in der Thermostatschicht und der Newtonschen Schicht folgen dem zweiten Newtonschen Gesetz. Eine periodische Grenze wurde entlang y . angewendet Richtung. Vor der Kratzsimulation wurden die Modelle durch NVE-Ensemble mit Berendsen-Thermostat-Methode entspannt. Vor den Kratzsimulationen wurde eine Relaxationszeit von 50 ps angewendet, um einen stabilen Energiezustand zu erhalten. Die Schleifform ist eine dreieckige Pyramide mit sphärischer Krone mit einem Kantenwinkel von 90°. Wie in Fig. 2 gezeigt, wurden die gemeinsamen Kristallebenen (a-Ebene (Grundebene), m-Ebene (prismatische Ebene) und c-Ebene) für 6H-SiC als Bearbeitungsoberflächen ausgewählt. Unter Berücksichtigung der Symmetrie der Struktur wurden folgende Ebenen-/Orientierungskombinationen als Bearbeitungsfläche/Bearbeitungsrichtung gewählt:\( (0001)/\left[2\overline{1}\overline{1}0\right]\), \( (0001)/\left[10\overline{1}0\right]\), \( \left(01\overline{1}0\right)/\left[2\overline{1}\overline{ 1}0\right] \), \( \left(01\overline{1}0\right)/\left[0001\right] \), \( \left(11\overline{2}0\right) /\left[1\overline{1}00\right]\) und \(\left(11\overline{2}0\right)/\left[0001\right]\). Die Bearbeitungsparameter der Simulation sind in Tabelle 1 aufgeführt. Vor der Ritzsimulation wurden die Schleifmittel auf der linken Seite des Werkstücks platziert und die Schleifspitze befindet sich 50 Å unter der oberen Oberfläche des Werkstücks. Der kleinste Abstand zwischen den Schleifmitteln und dem Werkstück beträgt 30 , was weit vom Grenzbereich des Wechselwirkungspotentials entfernt ist. Das Schleifmittel bewegt sich vom freien Ende des Werkstücks in positiver Richtung von x -Achse und schließen Sie den Ritzvorgang ab.

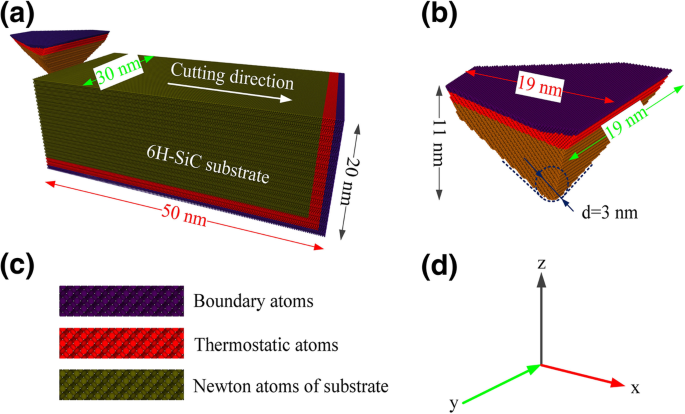
a MD-Modell der Nanoscratching-Simulation. b Die Morphologie des Werkzeugs. c Struktur des Modells. d Achsrichtung

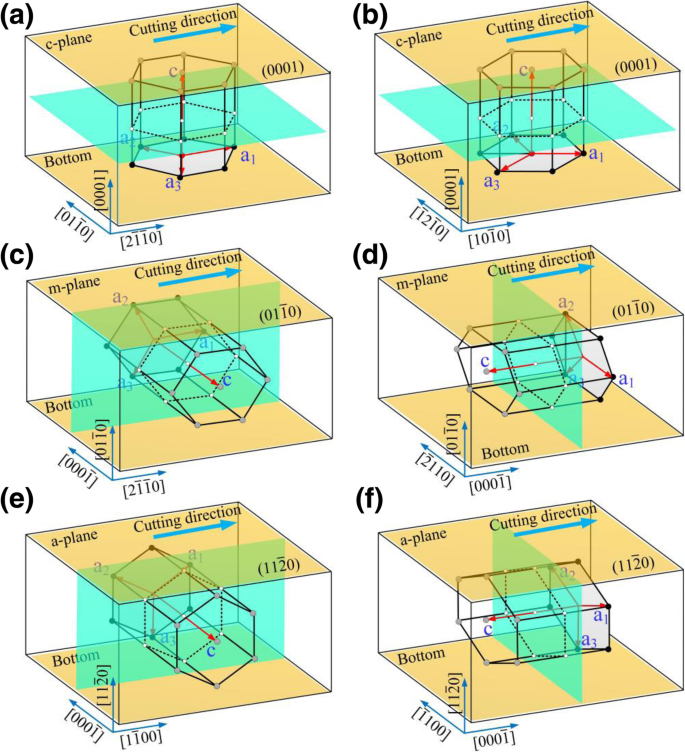
Schematische Darstellung des Ritzvorgangs, wobei a –f sind die entsprechenden Prozessmodi \( (0001)/\left[2\overline{1}\overline{1}0\right]\), \( (0001)/\left[10\overline{1}0\right ] \), \( \left(01\overline{1}0\right)/\left[2\overline{1}\overline{1}0\right] \), \( \left(01\overline{ 1}0\right)/\left[0001\right]\), \(\left(11\overline{2}0\right)/\left[1\overline{1}00\right]\), und \( \left(11\overline{2}0\right)/\left[0001\right] \), bzw.

Die Atompotentialfunktion spielt eine entscheidende Rolle für die Genauigkeit und Zuverlässigkeit der Molekulardynamiksimulation. Nach den bisherigen Tests und Simulationen zu den mechanischen Eigenschaften und Abtragsmechanismen von einkristallinem SiC ist die von Erhart und Albe [19] vorgeschlagene Funktion des analytischen Bindungsordnungspotentials (ABOP) für Wechselwirkungen zwischen Silizium und Kohlenstoff besser geeignet. Die in der Potentialfunktion verwendeten Parameter sind in Tabelle 2 gezeigt [19]. Anstelle der Tersoff-Potentialenergiefunktion [6] wird die ABOP-Potentialfunktion verwendet, um die Si-Si-, CC- und Si-C-Wechselwirkungen in und zwischen Werkzeug und Werkstück während der Bearbeitung zu definieren [2, 7, 8, 10, 11].

Ergebnisse und Diskussion

Nanometrische Zerspanbarkeitsanalyse

Wie in den Abb. 3 und 4 gezeigt, hatte die Anisotropie von 6H-SiC einen signifikanten Einfluss auf die nanometrische Bearbeitbarkeit (bearbeitete Tiefe, Entfernungsmodus, Entfernungsmenge und Tiefe der Beschädigung unter der Oberfläche (SSD) usw.). Entsprechend der Beziehung zwischen Bearbeitungsfläche/Bearbeitungsrichtung und Grundebene/c -Achse (siehe Abb. 3) lassen sich die Materialbearbeitungsmodi in drei Kategorien einteilen:(i) die Grundebene wird als Bearbeitungsfläche gewählt, (ii) die Grundebene steht senkrecht zur Bearbeitungsfläche und c -Achse senkrecht zur Bearbeitungsrichtung steht und (iii) die c -Achse ist parallel zur Bearbeitungsrichtung.

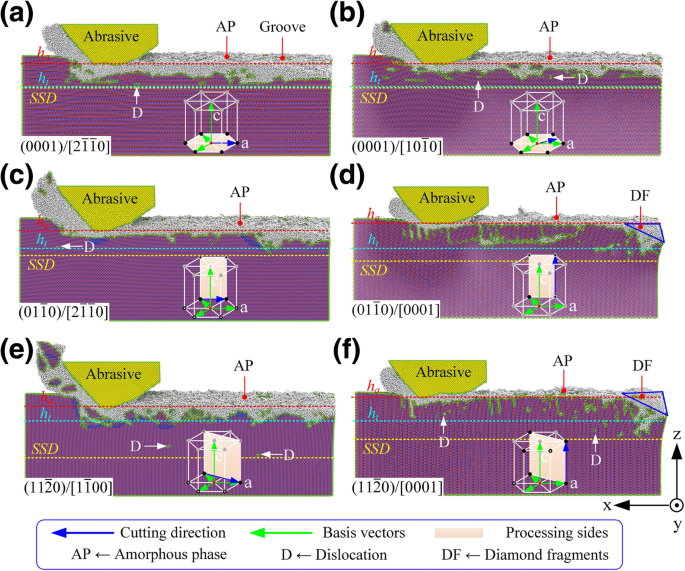
Topographie der bearbeiteten Oberfläche unter verschiedenen Kristallebenen-/Orientierungsbedingungen, wobei a –f sind die entsprechenden Prozessmodi \( (0001)/\left[2\overline{1}\overline{1}0\right]\), \( (0001)/\left[10\overline{1}0\right ] \), \( \left(01\overline{1}0\right)/\left[2\overline{1}\overline{1}0\right] \), \( \left(01\overline{ 1}0\right)/\left[0001\right]\), \(\left(11\overline{2}0\right)/\left[1\overline{1}00\right]\), und \( \left(11\overline{2}0\right)/\left[0001\right] \), bzw.

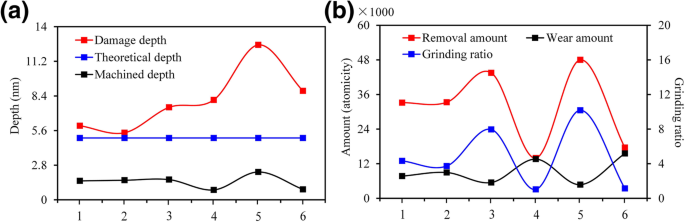
Nanometrische Bearbeitbarkeit unter verschiedenen Kristallebenen-/Orientierungsbedingungen, a der Einfluss der Anisotropie auf die Bearbeitungstiefe und die Schadenstiefe, b den Einfluss der Anisotropie auf Abtragsmenge, Verschleißmenge und Schleifverhältnis. 1, 2, 3, 4, 5 und 6 sind die entsprechenden Prozessmethoden \( (0001)/\left[2\overline{1}\overline{1}0\right]\), \( (0001)/ \left[10\overline{1}0\right]\), \( \left(01\overline{1}0\right)/\left[2\overline{1}\overline{1}0\right] \), \( \left(01\overline{1}0\right)/\left[0001\right] \), \( \left(11\overline{2}0\right)/\left[1\ overline{1}00\right] \) bzw. \( \left(11\overline{2}0\right)/\left[0001\right] \). Die Schadensschichttiefe bezieht sich auf die maximale Tiefe der internen Defekte des Kristalls, die durch das Kratzen verursacht werden. Die theoretische Tiefe bezieht sich auf die voreingestellte Tiefe vor der Bearbeitung. Die Bearbeitungstiefe bezieht sich auf die Resttiefe nach dem Anritzen. Die Abtragsmenge bezieht sich auf die Anzahl der Atome, von denen das Werkstückmaterial abgetragen wird. Der Verschleiß bezieht sich auf den Unterschied in der Anzahl der Atome der Schleifkörner vor und nach dem Kratzen

(i) Wie in Abb. 3a, b gezeigt, war die nanometrische Bearbeitbarkeit von 6H-SiC extrem ähnlich, wenn der Verarbeitungsmodus als \((0001)/\left[2\overline{1}\overline{1}0 . ausgewählt wurde \right] \) und \( (0001)/\left[10\overline{1}0\right] \). Der Entfernungsprozess von 6H-SiC neigte jedoch eher zum Sprödigkeitsmodus, wenn der Verarbeitungsmodus als \((0001)/\left[10\overline{1}0\right]\) ausgewählt wurde. (ii) Wie in Fig. 3c, e gezeigt, wenn die Verarbeitungsmodi als \( \left(01\overline{1}0\right)/\left[2\overline{1}\overline{1}0 . ausgewählt wurden \right] \) und \( \left(11\overline{2}0\right)/\left[1\overline{1}00\right] \), waren die Bearbeitungstiefe und der Materialabtrag deutlich höher als die bei den anderen Verarbeitungsmethoden. Wie in Abb. 4 gezeigt, wird bei gleicher theoretischer Bearbeitungstiefe (h _t =5,0 nm) war der Zeitspan im Bearbeitungsmodus \( \left(11\overline{2}0\right)/\left[1\overline{1}00\right] \) 3,4 mal so hoch wie das im Bearbeitungsmodus \( \left(01\overline{1}0\right)/\left[0001\right] \). Das Materialbearbeitungsverhältnis (Abtragsmenge/Werkzeugverschleiß) betrug 10,1, aber die SSD unter diesem Bearbeitungsparameter war auch viel höher als unter anderen Bearbeitungsbedingungen und erreichte das 2,3-fache von \( (0001)/\left[10\overline{ 1}0\rechts]\). Auf den bearbeiteten Oberflächen und Chips befand sich eine große Anzahl von Nanokristalliten. Unter dieser Bedingung trat eine große Anzahl von spröden Ausfällen auf. Der Bearbeitungsmodus \( \left(11\overline{2}0\right)/\left[1\overline{1}00\right] \) ist nur für die Nanogroove-Bearbeitung geeignet, die eine hohe Bearbeitungseffizienz erfordert, aber unempfindlich gegenüber Schäden unter der Oberfläche. Das Zeitspanvolumen von \( \left(01\overline{1}0\right)/\left[2\overline{1}\overline{1}0\right] \) war ähnlich dem von \( \left (11\overline{2}0\right)/\left[1\overline{1}00\right]\), aber die SSD war nur 50% von letzterem. Außerdem war die Dicke der amorphen Schicht auf der bearbeiteten Oberfläche viel geringer als die von \( (0001)/\left[2\overline{1}\overline{1}0\right]\) und \( (0001) /\left[10\overline{1}0\right] \). Die Phasenverteilung unter der Oberfläche war gleichmäßig und die mechanischen Eigenschaften der gesamten Nut waren besser als bei den anderen Verarbeitungsverfahren. Daher ist der Bearbeitungsmodus \( \left(01\overline{1}0\right)/\left[0001\right] \) die beste Wahl für die Bearbeitung von Mikro-Nano-Rillen auf 6H-SiC-Oberflächen mit hoher Effizienz , hohe Präzision und niedrige SSD. (iii) Wie in den Fign. 3d, f, wenn die Bearbeitungsrichtung parallel zu c . war -Achse wurde die Spitze während der ersten Bearbeitungsphase stark abgenutzt. Obwohl die Bearbeitungstiefe und die Materialabtragsrate viel geringer waren als bei den anderen Bearbeitungsverfahren und das Materialbearbeitungsverhältnis nur etwa 1,0 betrug, wurde die SSD von \( \left(01\overline{1}0\right)/\left[ 0001\right] \) und \( \left(11\overline{2}0\right)/\left[0001\right] \) waren mehr als die von \( \left(01\overline{1} 0\right)/\left[2\overline{1}\overline{1}0\right]\). Es wird daher nicht empfohlen, \( \left(01\overline{1}0\right)/\left[0001\right] \) und \( \left(11\overline{2}0\right)/ \left[0001\right] \) bei der Bearbeitung von Mikro-Nano-Rillen auf der Oberfläche von 6H-SiC. Diese Modi zeigen jedoch eine ausgezeichnete Verschleißfestigkeit; Daher sind sie für die Spanfläche des einkristallinen SiC-Schneidwerkzeugs geeignet, das im Bereich der Ultrapräzisionsbearbeitung von Eisenmetallen breite Perspektiven bietet.

Analyse der Lippenbewegung und der Schadensverteilung unter der Oberfläche

Schmid-Faktoren-Verteilung im Ritzprozess basierend auf einer dreieckigen Pyramidenspitze

Die üblichen Gleitsysteme des hexagonalen Kristallsystems (siehe Fig. 4) umfassen hauptsächlich basales Gleiten, prismatisches Gleiten und pyramidenförmiges Gleiten. Die Rutschfestigkeit steht im Zusammenhang mit der generalisierten Stapelfehlerenergie (GSF) und dE _GSF /dx vs. (x /b ) der Gleitsysteme. Die Gleitbewegung würde auf der dichtesten Ebene und entlang der kürzesten Richtung auftreten [10]. Die bevorzugten Gleitsysteme im Grundschlupf sind Grundschlupf (Shuffle-Sets)/<\( 1\overline{1}00 \)> und Basalschlupf (Shuffle-Sets)/<\( 11\overline{2}0 \)> [20]. Da ersteres kein Zwischenenergieminimum besitzt, hat letzteres in den Simulationen und Experimenten Vorrang [20]. Daher sind die in dieser Arbeit betrachteten Gleitbewegungen wie folgt:basaler Schlupf (Shuffle Sets)/<\( 11\overline{2}0 \)> und prismatischer Schlupf und Schlupf. Abb. 5.

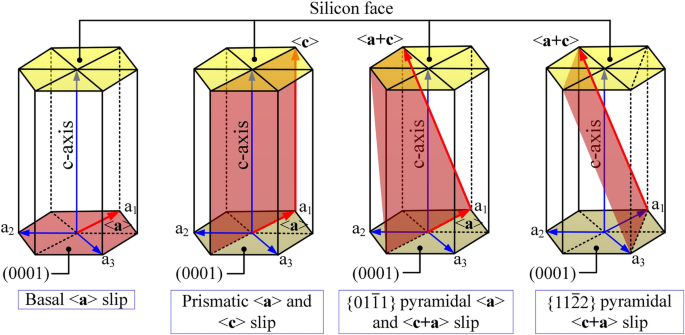
Gleitsysteme des Sechskantsystems

Die Schubspannungskomponente auf der Gleitebene τ _ss kann durch die Beziehung berechnet werden:

$$ {\tau}_{\mathrm{ss}}={\sigma}_{\mathrm{cont}}\mathit{\cos}<\overset{\rightharpoonup }{f},\overset{\rightharpoonup } {n_g}>\cos <\overset{\rightharpoonup }{f},\overset{\rightharpoonup }{t_g}>={\sigma}_{\mathrm{cont}}\bullet m $$ (1)

wo σ _weiter ist die Kontaktspannung, \( \overset{\rightharpoonup }{f} \) ist die Belastungsrichtung, \( \overset{\rightharpoonup }{n_g} \) und \( \overset{\rightharpoonup }{t_g} \) sind die Gleitebenennormale und Gleitrichtung im globalen kartesischen Koordinatensystem und m ist der Schmid-Faktor. Das globale Koordinatensystem wurde fixiert und das lokale Koordinatensystem mit der Richtung des Kristalls gedreht. Das x -Achse des lokalen Koordinatensystems war parallel zum Basisvektor \( \overset{\rightharpoonup }{a_1} \) während die z -Achse war parallel zum Basisvektor \( \overset{\rightharpoonup }{c} \).

Während des Ritzprozesses war die Hauptkontaktfläche der dreieckigen Pyramidenspitze die Spanfläche, aber wenn das Werkzeug stark abgenutzt war, ging die Hauptkontaktfläche in die Verbindung von Spanfläche und Spitzenspitze über. Die entsprechende Belastungsrichtung \( \overset{\rightharpoonup }{f} \) wird dargestellt als

$$ \left\{\begin{array}{c}\overset{\rightharpoonup }{f_1}=\left({f}_{1x},{f}_{1y},{f}_{1z} \right)\kern8em \mathrm{Rechen}\ \mathrm{Gesicht}\ \\ {}\overset{\rightharpoonup }{f_2}=\left({f}_{2x},{f}_{2y}, {f}_{2z}\right)\kern9.75em \mathrm{tip}\ \mathrm{top}\end{array}\right. $$ (2)

wobei \( \overset{\rightharpoonup }{f_1}=\left(1,0,-\sqrt{2}\right)\), \( \overset{\rightharpoonup }{f_2}=\left(0,0 ,-1\right) \) im globalen Koordinatensystem.

Als hexagonales Kristallsystem kann das Gleitsystem von 6H-SiC als {h k i l . ausgedrückt werden }/ < u v t w>. Die Gleitebenennormale \( \overset{\rightharpoonup }{n_c} \) und die Gleitrichtung \( \overset{\rightharpoonup }{t_c} \) im lokalen kartesischen Koordinatensystem sind dargestellt als

$$ \overset{\rightharpoonup }{n_c}=\left(\frac{3}{2}h,\frac{\sqrt{3}}{2}\left(h+2k\right),\frac{ 3 la}{2c}\right) $$ (3) $$ \overset{\rightharpoonup }{t_c}=\left(u-\frac{1}{2}\left(v+t\right),\ frac{\sqrt{3}}{2}\left(vt\right),\frac{c}{a}w\right) $$ (4)

Die Gleitebenennormale \( \overset{\rightharpoonup }{n_g} \) und die Gleitrichtung \( \overset{\rightharpoonup }{t_g} \) im globalen kartesischen Koordinatensystem werden dargestellt als

$$ \overset{\rightharpoonup }{n_g}=T\bullet \overset{\rightharpoonup }{n_c} $$ (4) $$ \overset{\rightharpoonup }{t_g}=T\overset{\rightharpoonup }{\ Kugel {t}_c} $$ (5)

wobei die Rotationsmatrixform vom globalen Koordinatensystem zum lokalen Koordinatensystem und die entsprechenden Rotationswinkel in Tabelle 3 gezeigt sind

Nach den Formeln (1)–(5) sind die Schmid-Faktoren der entsprechenden Gleitsysteme bei den Belastungsrichtungen \( \overset{\rightharpoonup }{f_1} \) und \( \overset{\rightharpoonup }{f_2} \ ) sind in Tabelle 4 gezeigt. (i) Der c/a-Wert von 6H-SiC erreichte 4,901, was viel größer als 1,633 ist. Daher war die erforderliche kritische Schubspannung für den Grundschlupf geringer als für das prismatische Gleitsystem. Wenn die bearbeitete Oberfläche eine Grundebene war, war der Koeffizient des Grundgleitsystems höher als der der anderen Gleitsysteme. Wenn also die Verarbeitungsmodi als \( (0001)/\left[2\overline{1}\overline{1}0\right] \) und \( (0001)/\left[10\overline{1 }0\right]\), fand zuerst die basale -Schlupfbewegung statt. (ii) Wenn die Verarbeitungsmodi als \( \left(01\overline{1}0\right)/\left[2\overline{1}\overline{1}0\right] \) und \( \ left(11\overline{2}0\right)/\left[1\overline{1}00\right]\), nur unter Berücksichtigung der Belastungsrichtungen \( \overset{\rightharpoonup }{f_1} \) und \( \overset{\rightharpoonup }{f_2} \), war der basale Schlupf theoretisch nicht möglich und die prismatische Gleitbewegung hatte Vorrang. (iii) Wenn die Verarbeitungsmodi als \( \left(01\overline{1}0\right)/\left[0001\right] \) und \( \left(11\overline{2}0\right )/\left[0001\right] \), wie in Abb. 4 gezeigt, war die Spitze während der ersten Verarbeitungsphase stark abgenutzt und \( \overset{\rightharpoonup }{f_2} \) spielte eine entscheidende Rolle in den Kratzprozess. Daher würde die Gleitbewegung im prismatischen Gleitsystem symmetrisch zur YOZ-Ebene in den globalen Koordinaten verteilt auftreten.

Oberflächen-/Untergrundschadensverteilung

Wie in Abb. 6a, b gezeigt, wenn \( (0001)/\left[2\overline{1}\overline{1}0\right]\) und \( (0001)/\left[01\overline{1 }0\right]\) gewählt wurden, erfolgte die Schlupfbewegung hauptsächlich auf dem Schlupfsystem \((0001)/<1\overline{2}10>\), was auf das Vorschieben des Werkzeugs zurückzuführen ist. Der entsprechende Gleitbewegungsmodus stimmt mit den Berechnungsergebnissen des Schmidt-Koeffizienten überein. Es gab nanokristalline Körner und Gitterdurchbiegungen im Untergrundbereich und diese Schäden bildeten einige unregelmäßige Gitterverzerrungszonen. Die amorphe Phase bedeckte die gesamte bearbeitete Oberfläche und die Tiefe der Versetzung lag nahe der Tiefe der Gitterverzerrungsschicht.

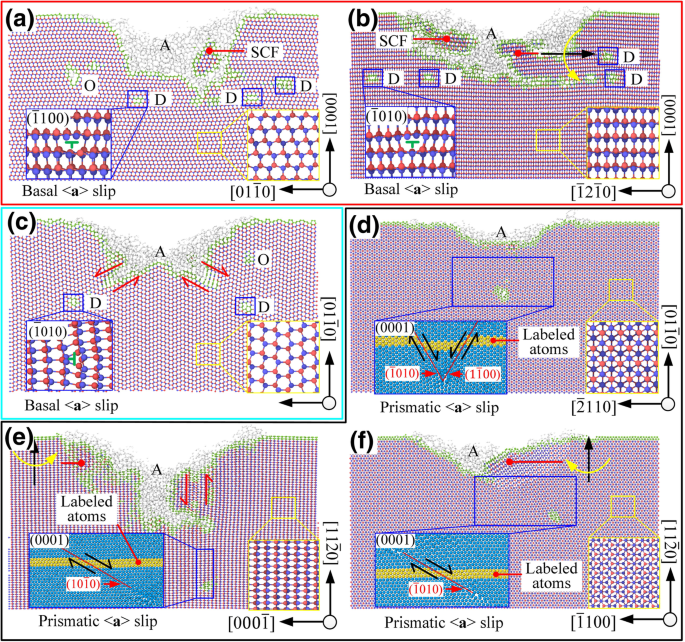
Der Querschnitt der bearbeiteten Fläche, D ist eine Luxation, A ist amorphe Phase, SCF ist einkristalline Form, O ist eine andere Art von Defekt, wobei a –f sind die entsprechenden Prozessmodi \( (0001)/\left[2\overline{1}\overline{1}0\right]\), \( (0001)/\left[10\overline{1}0\right ] \), \( \left(01\overline{1}0\right)/\left[2\overline{1}\overline{1}0\right] \), \( \left(01\overline{ 1}0\right)/\left[0001\right]\), \(\left(11\overline{2}0\right)/\left[1\overline{1}00\right]\), und \( \left(11\overline{2}0\right)/\left[0001\right]\) bzw.

Wenn \( \left(01\overline{1}0\right)/\left[2\overline{1}\overline{1}0\right] \) ausgewählt ist, als Schmidt-Basalkoeffizient < ein> Schlupf ist gleich 0, der Grundwert <a> Schlupf sollte theoretisch nicht vorkommen. Aber der Winkel zwischen Belastungsrichtung \( \overset{\rightharpoonup }{f_1} \) und Gleitrichtung \( \left[11\overline{2}0\right]\) betrug nur 5,3°. Unter der Scherwirkung aufgrund der Relativbewegung zwischen Kontaktfläche und Nichtkontaktfläche (siehe Abb. 6c) wird die basale <a> Schlupf wurde vor dem prismatischen Schlupf im Verarbeitungsmodus von \( \left(01\overline{1}0\right)/\left[2\overline{1}\overline{1}0\right] \) ausgelöst und trat auf beiden Seiten der V-Nut auf. Unter dem Verarbeitungsmodus \( \left(11\overline{2}0\right)/\left[1\overline{1}00\right] \) sind die Winkel zwischen der Belastungsrichtung \( \overset{\rightharpoonup }{f_1} \) und die Gleitrichtungen \( \left[1\overline{2}10\right] \) und \( \left[\overline{1}\overline{1}20\right] \) waren 24,7° bzw. 35,3°. Die Scherwirkung verursachte keine Gleitbewegung der Basalebene. Der entsprechende Schlupfmodus stimmt mit den Berechnungsergebnissen des Schmidt-Koeffizienten überein. Wie in Abb. 6e gezeigt, wenn \( \left(11\overline{2}0\right)/\left[1\overline{1}00\right]\) ausgewählt wurde, das Gleitsystem \( \left[ 1\overline{2}10\right]/\left(\overline{1}010\right)\) hatte einen hohen Schmidt-Koeffizienten unter der gemeinsamen Wirkung von \( \overset{\rightharpoonup }{f_1} \) und \ ( \overset{\rightharpoonup }{f_2} \), was zwangsläufig zu einer großen Tiefe der unterirdischen Schadensschicht führen würde. Die Gitterverzerrung und die amorphe Phase existierten auch, aber im Gegensatz zur Bearbeitung auf der Basisebene war die Versetzungstiefe signifikant größer als die der Gitterverzerrung. Die sp ³ →sp ² Übergangsverhalten trat im Untergrund auf.

Wenn die Verarbeitungsrichtung parallel zum c war -Achse, aufgrund des starken Verschleißes der Spitze, war prismatischer Schlupf, der durch die Abwärtsextrusion verursacht wurde, der primäre Gleitbewegungsmodus in der stabilen Kratzphase. Der entsprechende Schlupfmodus stimmte mit den Berechnungsergebnissen des Schmidt-Koeffizienten überein. Wenn \( \left(01\overline{1}0\right)/\left[0001\right] \) gewählt wurde, mit der Belastungsrichtung \( \overset{\rightharpoonup }{f_2} \), sind die Gleitsysteme \( \left[1\overline{2}10\right]/\left(\overline{1}010\right) \) und \( \left[\overline{1}\overline{1}20\right] /\left(1\overline{1}00\right)\) hatte den gleichen Schmidt-Koeffizienten, Kreuzschlupf trat auf den beiden Gleitflächen mit einem Winkel von 60° auf, und dann trat der Pinning-Effekt auf, der die Gleitbewegung behinderte . Somit ist die maximale Schadenstiefe unter der Oberfläche SSD _max wäre kleiner oder gleich h _t tan θ /2 cot α /2, wobei θ = 101° ist der theoretische Winkel der Nanorille und α = 60° ist der Winkel zwischen der Gleitebene \( \left(\overline{1}010\right) \) und \( \left(1\overline{1} 00\rechts)\). Bei Auswahl von \( \left(11\overline{2}0\right)/\left[0001\right] \) werden die Gleitsysteme \( \left[\overline{2}110\right]/\left( 0\overline{1}10\right)\) und \(\left[1\overline{2}10\right]/\left(\overline{1}010\right)\) hatten ebenfalls denselben Schmidt-Koeffizienten, aber die Rutschbewegung wurde durch den unregelmäßigen Verschleiß der Spitze beeinflusst und es trat nur das Rutschsystem \( \left[1\overline{2}10\right]/\left(\overline{1}010\right)\) auf.

Zusammenfassend waren, wie in Fig. 7 gezeigt, die Schäden in den unterirdischen Bereichen unter verschiedenen Verarbeitungsbedingungen hauptsächlich Versetzungen, Gitterverzerrung (Torsion/relatives Gleiten) und amorphe Phase. Die Verformung von 6H-SiC wurde hauptsächlich durch die Gleitbewegung, Nichtkristallisation von Materialien und unregelmäßige Gitterverzerrung verursacht. Die wichtigsten Gleitverformungsmodi waren der Grundschlupf und der prismatische Schlupf, die eng mit der Bearbeitungsoberfläche/-richtung verbunden sind.

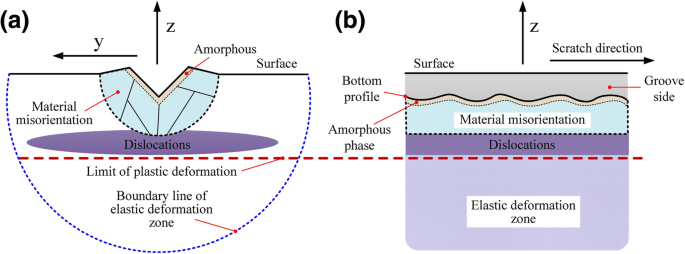
Verarbeitete Oberflächen-/Untergrund-Schadensverteilung. a xy Kreuzung. b xz Querschnitt