Beobachtung von Landau pegelabhängigen Aharonov-Bohm-ähnlichen Schwingungen in einem topologischen Isolator

Einführung

Die Aharonov-Bohm (AB)-Interferenz stammt von der Trägerwellenfunktionsinterferenz in einer Schleife, die ein gemusterter Ring [1, 2], eine geometrische Materialstruktur [3–6, 8–11] oder eine Trägertransporttrajektorie sein kann [12]. Das Magnetfeld, B , durch die Schleife induziert eine Phasenverschiebung der Trägerwellenfunktion, die zu periodischen Wellenfunktionsinterferenzoszillationen führt. Diese Oszillationsperiode ist empfindlich gegenüber den Trägertransporteigenschaften, wie der Trägerkohärenzlänge und -mobilität [3, 12]. Die Quanteninterferenz ist ein hervorragendes Werkzeug, um Materialtransporteigenschaften zu erkennen und intrinsische Mechanismen zu verstehen. Aufgrund der kurzen Trägerkohärenzlänge und des kleinen Flussquants wird die Quanteninterferenz hauptsächlich bei Nanodrähten mit hoher Mobilität oder strukturierten Nanoringen bei niedrigem B . berichtet [3–6, 8–11]. Berichte über ein makroskopisches System bei hohem B sind selten. Die Arbeiten zur AB-Quanteninterferenz bei hohem B weniger erforscht und der zugehörige Mechanismus ist weniger verstanden.

In dieser Arbeit wurden Quantenoszillationen in einem BiSbTe₃ . durchgeführt topologische Isolator-Makroflocke bei hohem B . Neben der Shubnikov-de Haas (SdH) Oszillation wurde die Aharonov-Bohm-ähnliche (ABL) Oszillation beobachtet. Die ABL-Schwingungsperiode beträgt B -abhängig und unterscheidet sich von der traditionellen AB-Schwingung, bei der die Schwingungsdauer unabhängig von B . ist . Die beobachtete ABL-Oszillationsperiode ist auf jedem Landau-Niveau (LL) konstant, das aus der SdH-Oszillation bestimmt wird. Die kürzeren Schwingungsperioden werden bei niedrigeren LLs beobachtet. Die Schwingungsdauer ist bei Temperaturen proportional zur Quadratwurzel der LL. Das Verhältnis der ABL-Schwingungsperiode zur effektiven Masse ist schwach LL-Abhängigkeit. Die LL-abhängige ABL-Schwingung könnte von der LL-abhängigen effektiven Masse herrühren.

Experimentelle Methode

Die Wachstumsbedingungen des BiSbTe₃ Einkristall ist derselbe wie unsere früheren Arbeiten zu den topologischen Isolatoren [13–16]. Unsere früheren Arbeiten haben gezeigt, dass mit der RHFZ-Methode TI mit extrem hoher Uniformität erhalten werden kann [13–16]. Raman-, EDS- und XPS-Spektrum bewiesen, dass es sich bei dem Kristall um BiSbTe₃ handelt . Die BiSbTe₃ Einkristallflocken wurden unter Verwendung des Scotch-Tape-Verfahrens erhalten. Die Geometrie der gespaltenen Flocken ist ungefähr 3 mm lang, 2 mm breit und 170 μ m dick. Magnetotransportmessungen wurden unter Verwendung der Standard-Sechs-Sonden-Technik in einem kommerziellen Gerät (Quantum Design PPMS) mit einem B . durchgeführt von bis zu 14 T. Die B senkrecht zur großen Spaltfläche aufgetragen. Die Datenpunkte werden pro 100 Gauss im Magnetfeldbereich zwischen 6 und 14 T im stationären Magnetfeldmodus statt im Sweep-Magnetfeldmodus aufgenommen.

Ergebnisse und Diskussion

Abbildung 1 zeigt die Magnetowiderstände (MRs) als Funktion von B . Die R (14T)/R (0T) erreicht 10 und ist höher als die meisten gemeldeten Werte in Bi _x Sb _2−x Te _y Se _3−y topologische Isolatoren [17–23, 23–33]. Sowohl theoretische als auch experimentelle Untersuchungen belegen, dass das MR-Verhältnis proportional zur Trägermobilität ist [34]. Das gemessene hohe MR-Verhältnis unterstützt die hohe Qualität unseres BiSbTe₃ Probe. Der Einschub oben links zeigt das d R /d B als Funktion von 1/B . Es zeigt, dass periodische Schwingungen und Schwingungsspitzen und -einbrüche gleich sind B bei 2 und 8 K. Dies wird als SdH-Oszillation bezeichnet, die von einem zweidimensionalen System ausgeht. Die SdH-Schwingungsperiode entspricht dem Fermi-Impulsvektor, k _f . Der Einschub rechts unten zeigt die schnelle Fourier-Transformation (FFT) der SdH-Oszillation. Sowohl für 2 als auch für 8 K wird ein scharfer Peak bei 48 T beobachtet. Nach der Onsager-Beziehung könnte man k . abschätzen _f bis \(F=\frac {\hbar k_{f}^{2}}{2e}\), wobei F ist die SdH-Schwingungsfrequenz. Die F =48 T führt zum k _f =3.8Å ⁻¹ , was mit dem beobachteten Wert von ARPES aus einer anderen Charge des gleichen Kristalls und mit in der Literatur angegebenen Werten übereinstimmt [35]. Das unterstützt die hohe Qualität und Einheitlichkeit unseres BiSbTe₃ Kristall. Neben der SdH-Oszillation zeigt der obere linke Einschub Schwingungen mit kurzer Periode. Um den Einfluss der SdH-Schwingung zu unterdrücken und Schwingungseigenschaften zu extrahieren, wird der d ² R /d B ² durchgeführt wird.

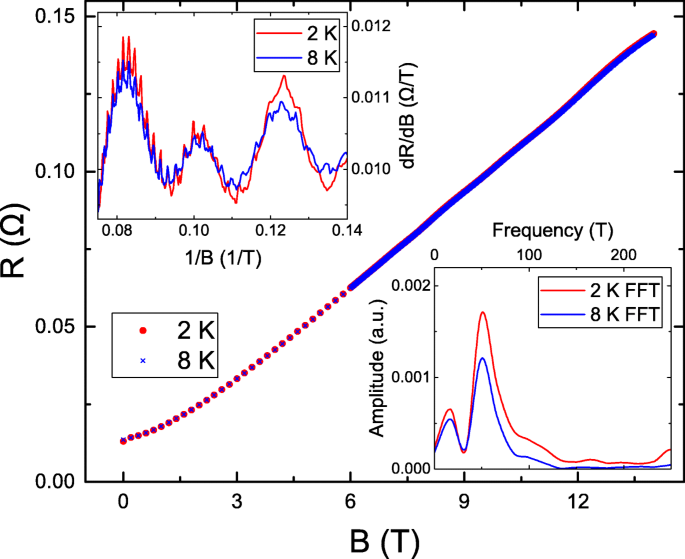
Der Magnetowiderstand als Funktion der Magnetfelder bei 2 und 8 K. Der obere linke Einschub zeigt das d R /d B als Funktion inverser Magnetfelder. Es zeigt eine periodische Schwingung. Der Einschub rechts unten zeigt die schnelle Fourier-Transformation der SdH-Oszillation und einen scharfen Peak bei 48 T sowohl für 2 als auch für 8 K

Abbildung 2 zeigt das d R /d B und d ² R /d B ² als Funktion von B bei 2 und 8 K. Punktlinien kennzeichnen Schwingungsspitzen in d ² R /d B ² , und lange Strichlinien entsprechen B von LLs, die aus der extrahierten SdH-Schwingungsfrequenz bestimmt werden. Die periodischen Schwingungen sind der AB-Schwingung ähnlich. Die AB-Schwingungsperiode wird als \(\Delta B =\frac {\Phi }{A}\) ausgedrückt. Φ ist das Flussquantum, wobei \(\frac {h}{e}\) und A ist der Geometriebereich, der von Taktzähl- und Antitaktzähl-Trägertrajektorien in einer begrenzten Struktur durchgeschleift wird. Aufgrund des kleinen Flussquants wird die AB-Oszillation hauptsächlich im Einschluss durch künstliche Nanostrukturen beobachtet [1, 2], wie Nanoringe und Nanodrähte [3–11]. Kürzlich wurde berichtet, dass die trägerelastische Streutrajektorie eine Reihe verbundener geschlossener Schleifen in einem makroskopischen System bilden könnte. A B Fluss durch diese Schleifen würde eine Phasenverschiebung der Trägerwellenfunktion induzieren und zu periodischen ABL-Oszillationen führen [12]. Die extrahierte elastische Streulänge beträgt ungefähr 150 nm, was der Schwingungsperiode mit 0,02 T entspricht und mit unserer experimentellen Beobachtung übereinstimmt.

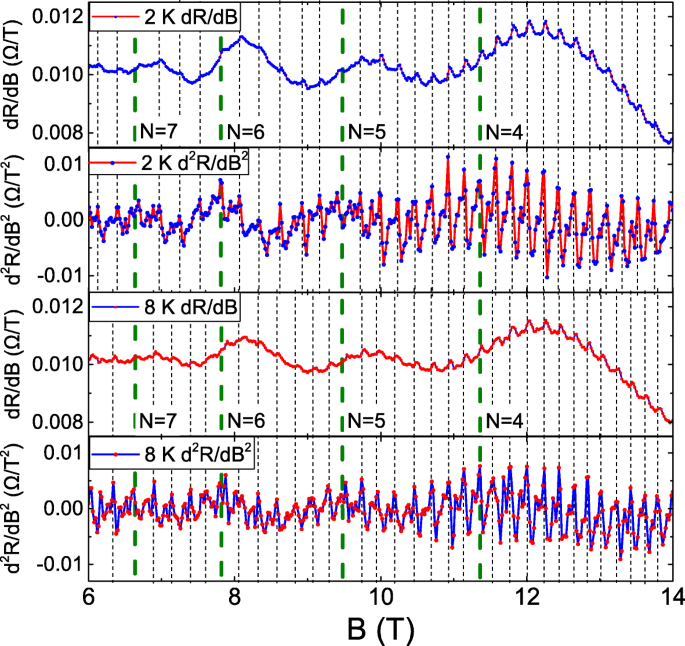
Die d R /d B und d ² R /d B ² als Funktion von B bei 2 und 8 K. Es zeigt periodische Schwingungen und die Schwingungsdauer ist vom Landau-Niveau abhängig

Den gepunkteten Linien in Abb. 2 folgend, könnte man feststellen, dass die Oszillationsperiode bei jeder LL konstant ist und die Oszillationsperiode bei niedrigeren LLs kürzer ist. Dieses Verhalten unterscheidet sich von der traditionellen AB-Oszillation. Um diese Schwingungsperioden zu extrahieren und zu bestimmen, wird FFT an verschiedenen LLs durchgeführt. Abbildung 3 zeigt die FFT bei verschiedenen LLs bei 2 und 8 K und zeigt deutlich die höhere Oszillationsfrequenz bei niedrigeren LLs bei 2 und 8 K.

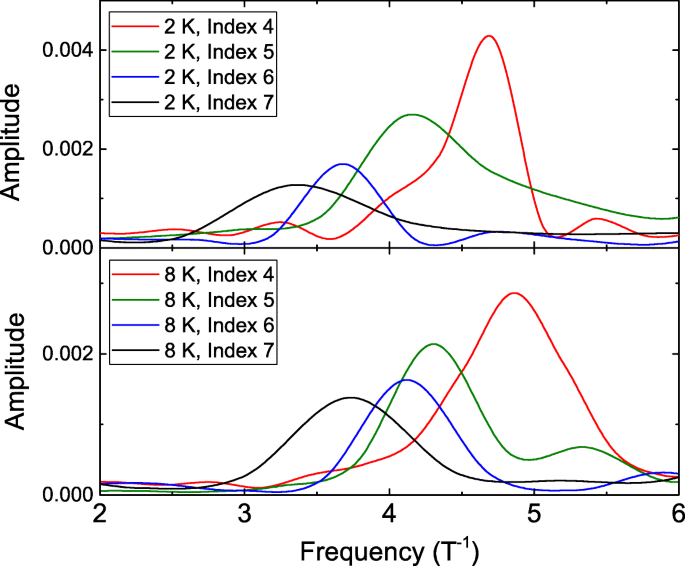
Die schnelle Fourier-Transformation des d R /d B bei unterschiedlichen Landauer Niveaus und Temperaturen. Die höhere Oszillationsfrequenzspitze wird bei niedrigeren Landau-Niveaus beobachtet

Eine ähnliche LL-abhängige ABL-Oszillation wird im ganzzahligen Quanten-Hall-Regime in zweidimensionalem Halbleiter-Elektronengas berichtet [36, 37]. Sie wurde entweder als konstruktive Interferenz eindimensionaler Elektronen, die entlang von Kantenkanälen wandern, oder als Quantenwelleninterferenz von Kantenelektronen interpretiert. Der Trägertransportpfad in verschiedenen Kantenkanälen führt zu unterschiedlichen effektiven Bereichen in einem begrenzten Muster und schließlich zu unterschiedlichen ABL-Oszillationsperioden in Kantenkanälen bei verschiedenen LLs [38–40]. Weitere Studien an elektrischen Fabry-Perot-Interferometern im ganzzahligen und fraktionierten Quanten-Hall-Regime zeigen, dass die ABL-Oszillationsperiode mit der Flussperiode durch \(\frac {\Phi }{f}\) zusammenhängt, wobei f ist das vollbesetzte LL in den Engstellen. Die Schwingungsperiode wird zu \(\frac {\Phi }{A f}\) erwartet, wobei A ist die Geometriefläche der begrenzten Form [41, 42].

Tabelle 1 listet die extrahierten Schwingungsperioden aus der FFT bei verschiedenen LLs und Temperaturen auf. Die Analyse zeigt, dass das Verhältnis der Schwingungsdauer zur Quadratwurzel von LL bei jeder Temperatur konstant ist. Dies unterscheidet sich vom Verhalten des Fabry-Perot-Interferometers, bei dem die Schwingung umgekehrt proportional zu den LLs ist [41, 42]. Andererseits entsteht die elektrische Fabry-Perot-Interferenz aus der Kopplung der Trägertrajektorie zwischen verschiedenen LLs von innerhalb und außerhalb eines begrenzten Musters [37]. Die Schwingung hängt stark von der gemusterten Geometrie ab. Es gibt keine künstlichen Muster auf der Oberfläche unserer Proben und es sollten keine geeigneten Kopplungskanäle zwischen verschiedenen LLs vorhanden sein. Darüber hinaus liegen die Geometriegrößen unserer Proben im Millimeterbereich und die zugehörige AB-Schwingungsperiode wäre zu klein, um erfasst zu werden. Trotz dieser Unterschiede zu bestehenden Arbeiten denken wir, dass neben der geometrischen Fläche und der Trägerkohärenzlänge die intrinsische Trägercharakteristik eine kritische Rolle bei der LL-abhängigen ABL-Oszillation spielen könnte [3, 43].

Der Lifshitz-Kosevich (LK)-Theorie folgend, kann man charakteristische Parameter der Transportträger im Oberflächenzustand des topologischen Isolators extrahieren, und die Temperaturabhängigkeit der Amplitude der SdH-Oszillation wird ausgedrückt als

wobei \(\lambda(T/B) =(2\pi^{2}k_{B}Tm_{cyc})/(\hbar eB)\). Abbildung 4 zeigt die extrahierte normalisierte SdH-Oszillationsamplitude als Funktion der Temperatur bei verschiedenen LLs. Es stimmt gut mit der LK-Theorie überein und zeigt unterschiedliche Tendenzen bei verschiedenen LLs. Die Anpassungsergebnisse belegen, dass die m _zyk =0,152m ₀ ,0,170m ₀ ,0,185m ₀ , und 0,191m ₀ , wo m ₀ ist die freie Elektronenmasse, für N =4, 5, 6 bzw. 7. Diese Werte stimmen mit den berichteten effektiven Massen in topologischen Isolatoren überein [21, 22]. Diese vom Landau-Niveau abhängige effektive Masse wurde kürzlich im 3D-Dirac-Halbmetall ZrTe₅ . beobachtet [44]. Der Ursprung der magnetfeldabhängigen effektiven Masse ist jedoch noch nicht klar. Es bedarf weiterer Untersuchungen, um den intrinsischen Mechanismus zu klären. Die unterschiedliche effektive Masse würde die intrinsische Trägertransportcharakteristik an der Fermi-Oberfläche, wie die Fermi-Geschwindigkeit, die direkt mit der Kohärenzlänge der Trägerphase zusammenhängt, direkt abweichen. Die höhere effektive Masse würde zu einer geringeren Kohärenzlänge führen, die der längeren AB-ähnlichen Schwingungsperiode entspricht. Dies stimmt qualitativ mit unserer experimentellen Beobachtung überein. Wie in Tabelle 1 gezeigt, zeigt das Verhältnis der AB-ähnlichen Oszillationsperiode zur effektiven Masse eine schwache LL-Abhängigkeit. Die vom Landau-Niveau abhängige effektive Masse könnte einer der intrinsischen Effekte sein, der zu der LL-abhängigen Schwingungsperiode führt.

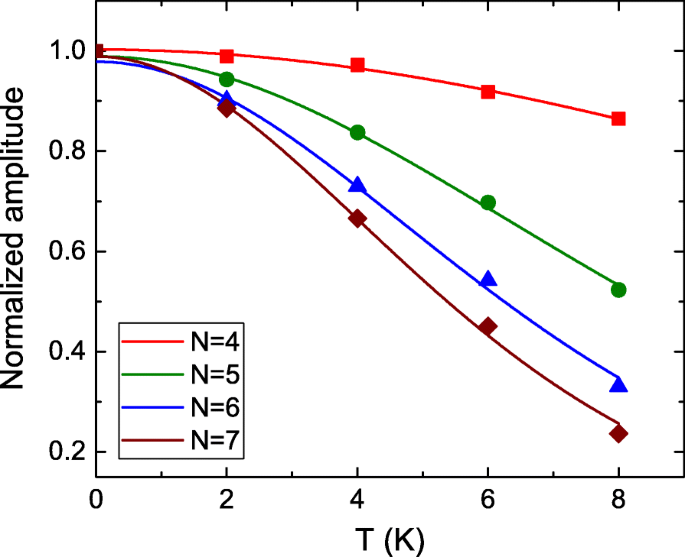
Die extrahierte normalisierte SdH-Schwingungsamplitude als Funktion der Temperatur auf verschiedenen Landau-Niveaus. Es stimmt gut mit der LK-Theorie überein und zeigt unterschiedliche Tendenzen auf verschiedenen Landau-Niveaus

LL ist eine Transportcharakteristik eines zweidimensionalen Systems. Dies deutet darauf hin, dass die LL-abhängige Oszillation möglicherweise vom Oberflächenzustandsträger in TIs stammt. Die Beerenphase ist ein Merkmal von Transportunternehmen. Das Extrahieren der Berry-Phase könnte helfen, die Quelle dieser LL-abhängigen periodischen AB-Oszillationen zu identifizieren. Wir definieren die AB-Schwingungsindexzahl, indem wir das entsprechende B . dividieren von Schwingungsspitzen in d B /d B um die zugehörige Schwingungsdauer im LL. Es zeigt, dass die Indexzahl der Oszillationsspitzen in d B /d B entspricht N +0,25, wobei N ganzzahlig ist, für alle Schwingungen in verschiedenen LLs und Temperaturen. Dies unterstützt weiter, dass die AB-Oszillationsperiode mit LLs zusammenhängt. Abbildung 5 zeigt, dass die AB-Schwingungsindexzahlen proportional zu B . sind bei verschiedenen LLs und Temperaturen. Der Achsenabschnitt beträgt 0,25, was eine Phasenverschiebung von 0,5 in der Auftragung der AB-Oszillation anzeigt. Dies unterstützt die Berry-Phase ist π und die beobachteten AB-Oszillationen könnten die Ladungsträgertransportcharakteristik des Oberflächenzustands in unserem BiSbTe₃ . sein topologischer Isolator [45].

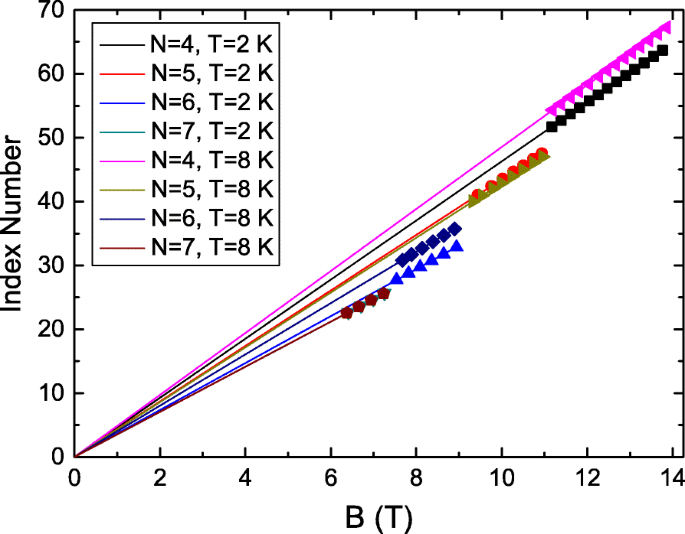
Die AB-Schwingungsindexzahl als Funktion von B bei unterschiedlichen Landauer Niveaus und Temperaturen. Der Achsenabschnitt beträgt 0,25, was eine Phasenverschiebung von 0,5 in der Auftragung der AB-Oszillation anzeigt. Dies unterstützt die Berry-Phase ist π

Schlussfolgerung

Wir haben die Quantenoszillationen in einem BiSbTe₃ . berichtet topologische Isolator-Makroflocke. Neben der Shubnikov-de Haas (SdH) Oszillation zeigt es eine Aharonov-Bohm-ähnliche (ABL) Oszillation. Die ABL-Schwingungsperiode beträgt B -abhängig. Die ABL-Schwingungsperiode ist auf jedem Landau-Niveau (LL) konstant. Die kürzeren Schwingungsperioden wurden bei niedrigeren LLs beobachtet, was durch die SdH-Oszillation bestimmt wurde. Die Schwingungsdauer ist bei verschiedenen Temperaturen proportional zur Quadratwurzel der LL. Das Verhältnis der ABL-Schwingungsperiode zur effektiven Masse ist schwach LL-Abhängigkeit. Die LL-abhängige ABL-Schwingung könnte von der LL-abhängigen effektiven Masse herrühren.

Verfügbarkeit von Daten und Materialien

Die während der laufenden Studie generierten und/oder analysierten Datensätze sind auf begründete Anfrage bei den entsprechenden Autoren erhältlich.

Abkürzungen

EDS:

Energiedispersive Röntgenspektroskopie

XPS:

Röntgenphotoelektronenspektroskopie

ARPES:

Winkelaufgelöste Photoemissionsspektroskopie

SdH:

Shubnikov-de Haas