Halbaddierer
Lassen Sie uns als erstes Beispiel für eine nützliche kombinatorische Logik ein Gerät bauen, das zwei Binärziffern addieren kann. Wir können schnell berechnen, wie die Antworten aussehen sollten:
0 + 0 =0 0 + 1 =1 1 + 0 =1 1 + 1 =102
Wir benötigen also zwei Eingänge (a und b) und zwei Ausgänge. Die Ausgabe niedriger Ordnung wird als Σ bezeichnet, weil sie die Summe darstellt, und die Ausgabe hoher Ordnung wird als Cout . bezeichnet weil es die Durchführung darstellt. Die Wahrheitstabelle ist:
ABΣCout 0000011010101101
Wenn Sie boolesche Gleichungen vereinfachen oder eine Karnaugh-Karte erstellen, erhalten Sie dieselbe Schaltung wie unten gezeigt, aber beginnen Sie mit dem Betrachten der Ergebnisse. Die Spalte Σ ist unser bekanntes XOR-Gatter, während die Cout Spalte ist das UND-Gatter. Dieses Gerät wird aus Gründen, die im nächsten Abschnitt sinnvoll sind, als Halbaddierer bezeichnet.
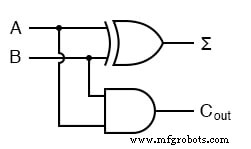
oder in Kontaktplanlogik
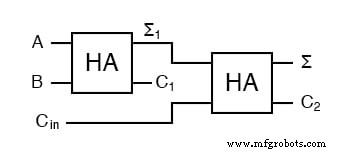
VERWANDTES ARBEITSBLATT:
-
Arbeitsblatt für binäre mathematische Schaltkreise
Industrietechnik



