Einführung in kombinatorische Logikfunktionen

Der Begriff „Kombination“ stammt aus der Mathematik. In der Mathematik ist eine Kombination eine ungeordnete Menge, was formal ausdrückt, dass es niemanden interessiert, in welcher Reihenfolge die Gegenstände eingehen. Die meisten Spiele funktionieren auf diese Weise, wenn Sie nacheinander würfeln und eine 2 gefolgt von einer 3 erhalten, ist dies der Fall das gleiche, als ob Sie eine 3 gefolgt von einer 2 gewürfelt hätten. Mit kombinatorischer Logik erzeugt die Schaltung unabhängig von der Reihenfolge, in der die Eingaben geändert werden, die gleiche Ausgabe.

Es gibt Schaltungen, die davon abhängen, wann sich die Eingänge ändern, diese Schaltungen werden als sequentielle Logik bezeichnet. Auch wenn Sie den Begriff „sequentielle Logik“ nicht in den Kapitelüberschriften finden, werden die nächsten Kapitel die sequentielle Logik behandeln.

Praktische Schaltungen haben eine Mischung aus kombinatorischer und sequentieller Logik, wobei sequentielle Logik sicherstellt, dass alles in der richtigen Reihenfolge passiert, und kombinatorische Logik Funktionen wie Arithmetik, Logik oder Konvertierung ausführt.

Sie haben bereits kombinatorische Schaltungen verwendet. Jedes zuvor diskutierte Logikgatter ist eine kombinatorische Logikfunktion. Lassen Sie uns verfolgen, wie zwei NAND-Gatter funktionieren, wenn wir ihnen Eingänge in unterschiedlicher Reihenfolge bereitstellen.

Wir beginnen damit, dass beide Eingaben 0 sind.

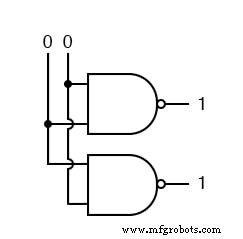
Dann setzen wir einen Eingang hoch.

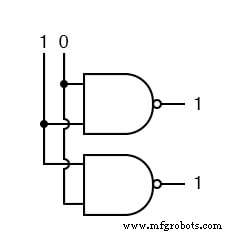
Dann setzen wir den anderen Eingang hoch.

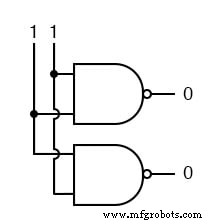
NAND-Gatter kümmern sich also nicht um die Reihenfolge der Eingänge, und Sie werden dasselbe Verhalten wie alle anderen bis zu diesem Punkt behandelten Gatter feststellen (AND, XOR, OR, NOR, XNOR und NOT).

VERWANDTES ARBEITSBLATT:

• Arbeitsblatt zur Booleschen Algebra