Leistung in ohmschen und reaktiven Wechselstromkreisen

Betrachten Sie einen Stromkreis für ein einphasiges Wechselstromsystem, bei dem eine 120-Volt-, 60-Hz-Wechselspannungsquelle Strom an eine ohmsche Last liefert:(Abbildung unten)

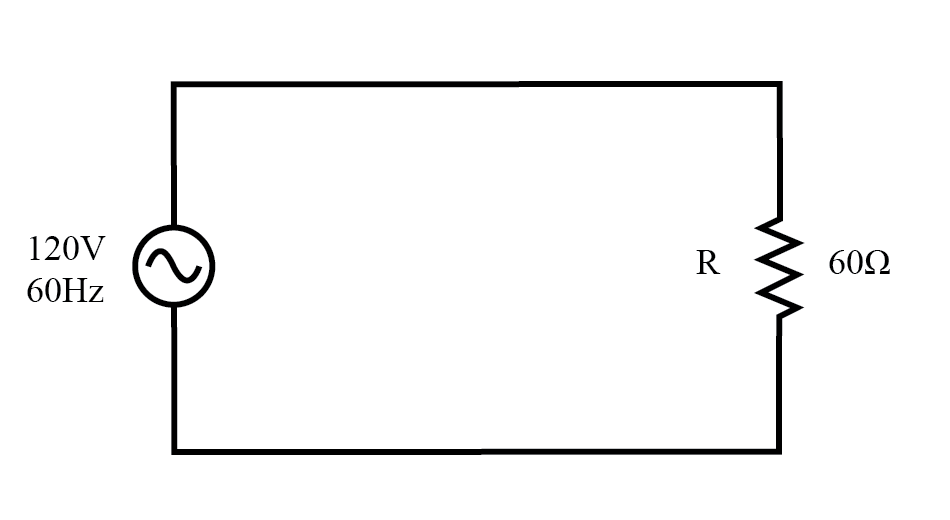
Ac-Quelle treibt eine rein ohmsche Last.

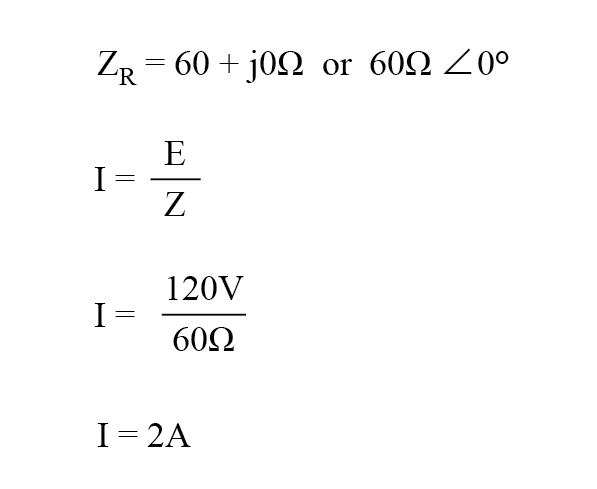
In diesem Beispiel würde der Strom zur Last 2 Ampere RMS betragen. Die Verlustleistung an der Last würde 240 Watt betragen.

Da diese Last rein ohmsch ist (keine Reaktanz), ist der Strom in Phase mit der Spannung, und die Berechnungen ähneln denen in einem äquivalenten Gleichstromkreis.

Wenn wir die Spannungs-, Strom- und Leistungswellenformen für diese Schaltung darstellen würden, würde sie wie in der folgenden Abbildung aussehen.

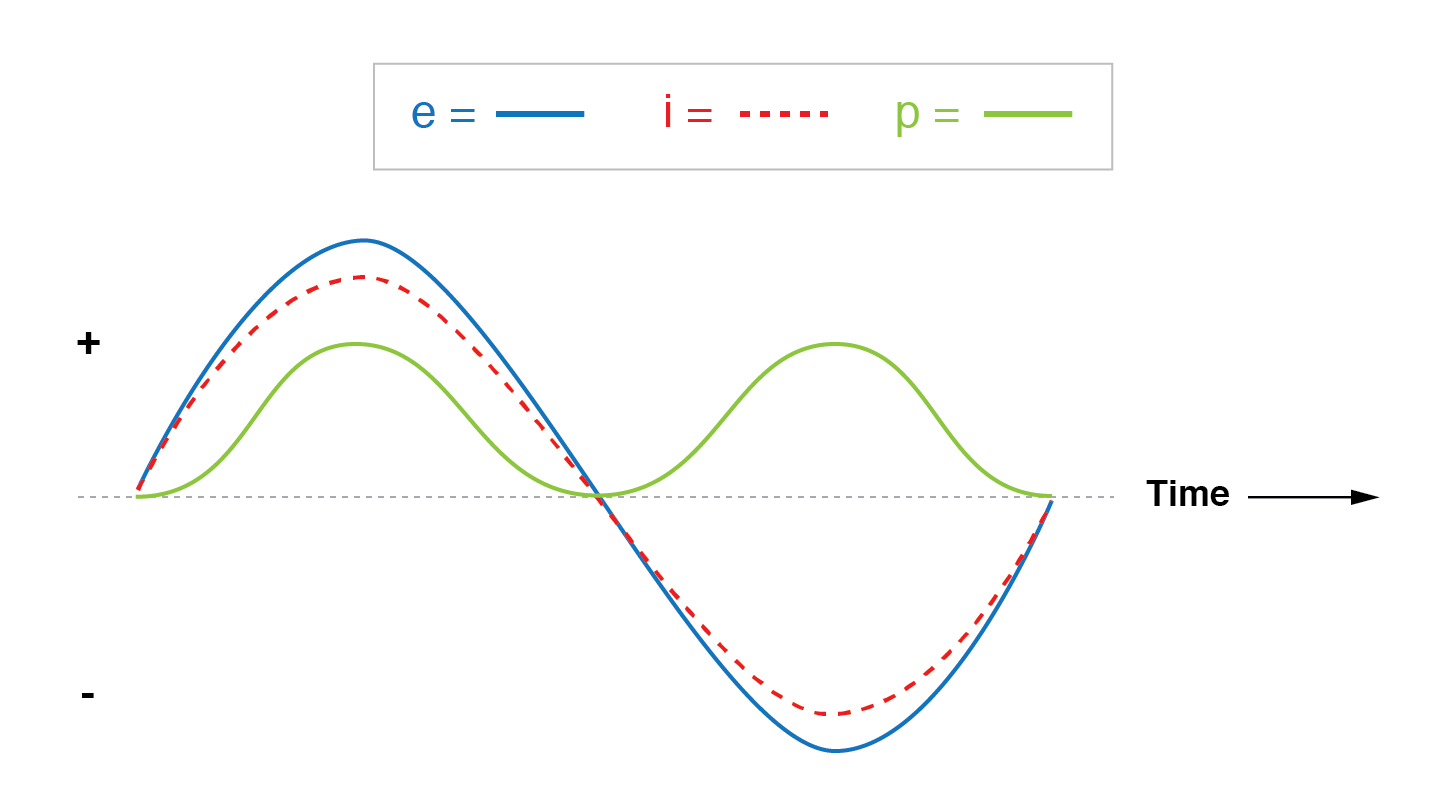
Der Strom ist in einem Widerstandskreis in Phase mit der Spannung.

Beachten Sie, dass die Wellenform für die Leistung bei dieser Widerstandsschaltung immer positiv und niemals negativ ist.

Dies bedeutet, dass Leistung immer von der ohmschen Last abgeführt und nie wie bei Blindlasten an die Quelle zurückgegeben wird. Wenn die Quelle ein mechanischer Generator wäre, würde es 240 Watt mechanischer Energie (etwa 1/3 PS) erfordern, um die Welle zu drehen.

Beachten Sie auch, dass die Wellenform für die Leistung nicht dieselbe Frequenz wie die Spannung oder der Strom hat! Stattdessen ist seine Häufigkeit doppelt die der Spannungs- oder Stromwellenformen.

Diese unterschiedliche Frequenz verbietet unseren Leistungsausdruck in einem Wechselstromkreis mit der gleichen komplexen (rechteckigen oder polaren) Schreibweise wie für Spannung, Strom und Impedanz, da diese Form der mathematischen Symbolik unveränderliche Phasenbeziehungen impliziert.

Wenn die Frequenzen nicht gleich sind, ändern sich die Phasenbeziehungen ständig.

So seltsam es auch erscheinen mag, der beste Weg, um mit der Berechnung der Wechselstromleistung fortzufahren, ist die Verwendung von Skalar Notation und um alle relevanten Phasenbeziehungen mit Trigonometrie zu behandeln.

Wechselstromkreis mit rein reaktiver Last

Betrachten wir zum Vergleich in der folgenden Abbildung einen einfachen Wechselstromkreis mit einer reinen Blindlast.

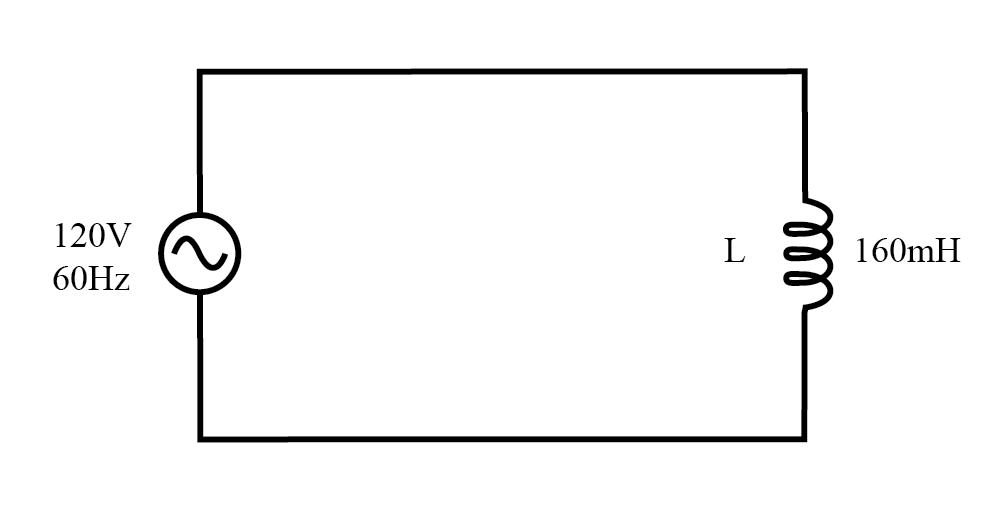
Wechselstromkreis mit rein reaktiver (induktiver) Last.

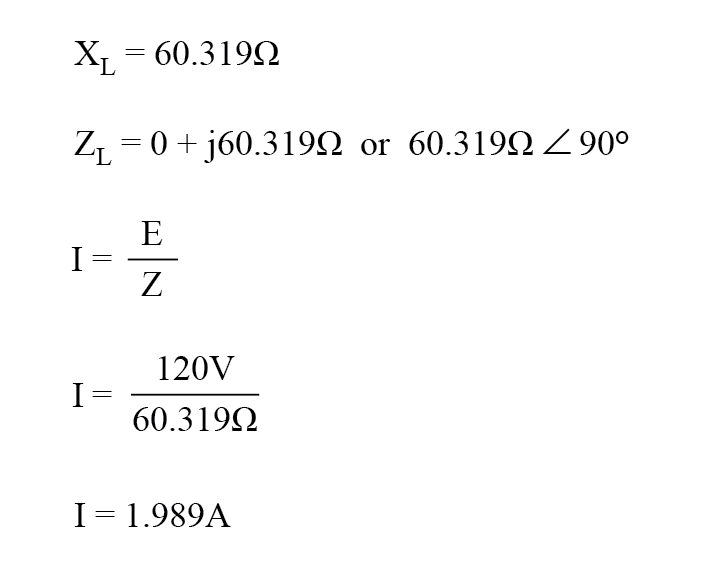
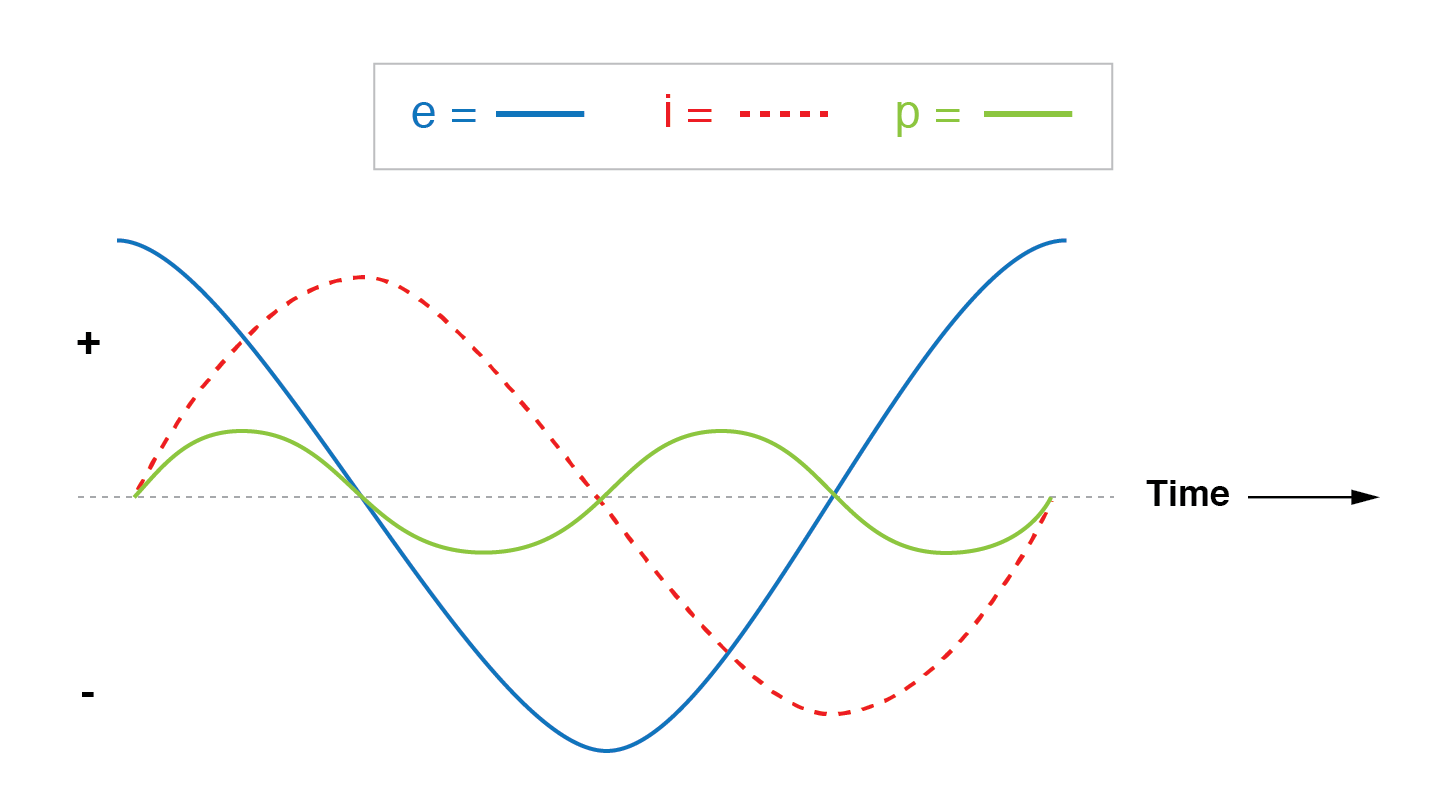
Leistung wird bei einer rein reaktiven Last nicht abgebaut. Obwohl es abwechselnd von der Quelle absorbiert und zu ihr zurückgeführt wird.

Beachten Sie, dass die Leistung zwischen positiven und negativen Zyklen gleichmäßig wechselt. (Abbildung oben) Dies bedeutet, dass Leistung abwechselnd von der Quelle aufgenommen und an sie zurückgegeben wird.

Wenn die Quelle ein mechanischer Generator wäre, würde (praktisch) keine mechanische Nettoenergie benötigt, um die Welle zu drehen, da keine Leistung von der Last verbraucht würde.

Die Generatorwelle wäre leicht zu drehen und der Induktor würde sich nicht wie ein Widerstand erwärmen.

Wechselstromkreis mit ohmscher und rein reaktiver Last

Betrachten wir nun in der folgenden Abbildung einen Wechselstromkreis mit einer Last, die sowohl aus Induktivität als auch aus Widerstand besteht.

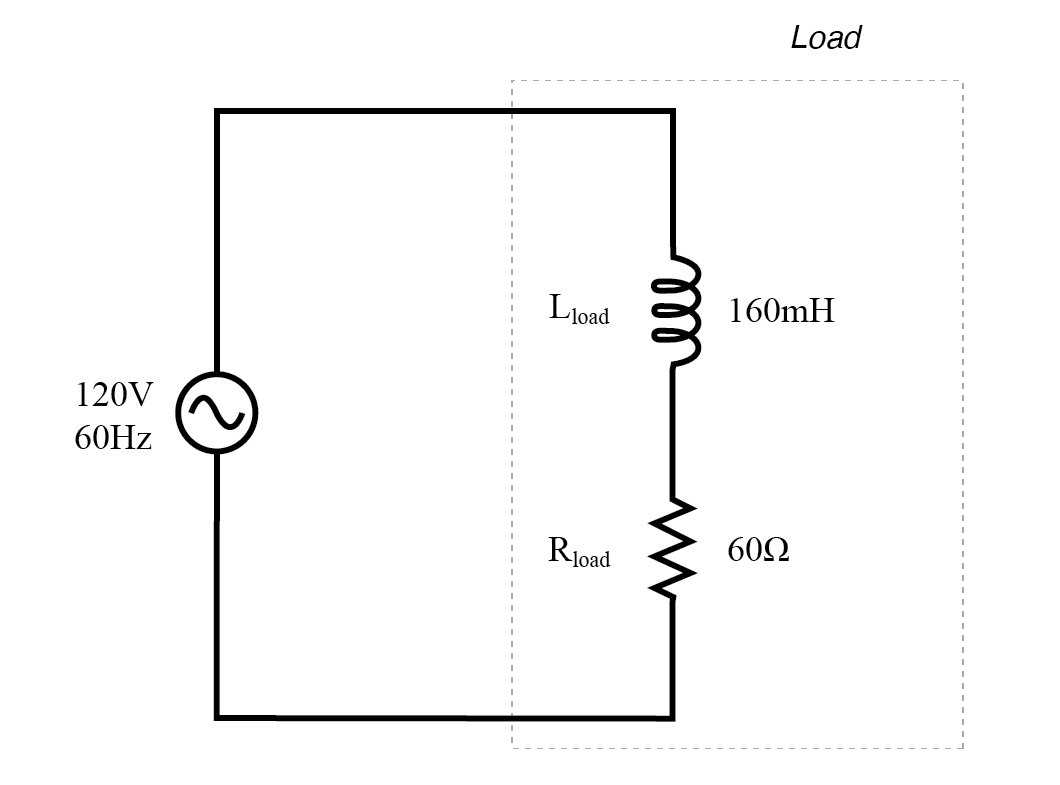
Wechselstromkreis mit Reaktanz und Widerstand.

Bei einer Frequenz von 60 Hz ergeben die 160 Millihenry Induktivität 60,319 Ω induktive Reaktanz.

Diese Reaktanz kombiniert mit dem Widerstand von 60 Ω ergibt eine Gesamtlastimpedanz von 60 + j60,319 Ω oder 85,078 Ω ∠ 45,152 ^o . Wenn wir uns nicht mit Phasenwinkeln beschäftigen (was wir an diesem Punkt nicht tun), können wir den Strom in der Schaltung berechnen, indem wir die Polargröße der Spannungsquelle (120 Volt) nehmen und sie durch die Polargröße der Impedanz dividieren (85.078 ).

Bei einer Versorgungsspannung von 120 Volt RMS beträgt unser Laststrom 1,410 Ampere. Dies ist die Zahl, die ein RMS-Amperemeter anzeigen würde, wenn es mit dem Widerstand und der Induktivität in Reihe geschaltet wäre.

Wir wissen bereits, dass Blindkomponenten keine Leistung verbrauchen, da sie gleichermaßen Leistung vom Rest der Schaltung absorbieren und an sie zurückgeben.

Daher wird jede induktive Reaktanz in dieser Last ebenfalls keine Leistung verbrauchen.

Hier bleibt nur noch der ohmsche Anteil der Lastimpedanz zur Verlustleistung. Wenn wir uns das Wellenformdiagramm von Spannung, Strom und Gesamtleistung für diese Schaltung ansehen, sehen wir in der folgenden Abbildung, wie diese Kombination funktioniert.

Eine kombinierte Widerstands-/Reaktionsschaltung verbraucht mehr Energie, als sie an die Quelle zurückgibt. Die Reaktanz verbraucht keine Leistung; Der Widerstand tut es jedoch.

Wie bei jedem Blindstromkreis wechselt die Leistung mit der Zeit zwischen positiven und negativen Momentanwerten.

In einem reinen Blindstromkreis wird dieser Wechsel zwischen positiver und negativer Leistung gleichmäßig aufgeteilt, was zu einer Nettoverlustleistung von Null führt. In Schaltungen mit gemischtem Widerstand und Reaktanz wie dieser wechselt die Leistungswellenform jedoch immer noch zwischen positiv und negativ, aber die Menge der positiven Leistung wird die Menge der negativen Leistung überschreiten.

Mit anderen Worten, die kombinierte induktive/ohmsche Last verbraucht mehr Strom, als sie zur Quelle zurückgibt.

Wenn man sich das Wellenformdiagramm für die Leistung ansieht, sollte klar sein, dass die Welle mehr Zeit auf der positiven Seite der Mittellinie verbringt als auf der negativen, was darauf hindeutet, dass mehr Leistung von der Last absorbiert als an den Stromkreis zurückgegeben wird.

Die geringe Leistungsrückkehr, die auftritt, ist auf die Reaktanz zurückzuführen; Das Ungleichgewicht zwischen positiver und negativer Leistung ist auf den Widerstand zurückzuführen, da er Energie außerhalb des Stromkreises ableitet (normalerweise in Form von Wärme).

Wenn die Quelle ein mechanischer Generator wäre, wäre die zum Drehen der Welle benötigte Menge an mechanischer Energie die Menge an Leistung, die zwischen den positiven und negativen Leistungszyklen gemittelt wird.

Die mathematische Darstellung von Leistung in einem Wechselstromkreis ist eine Herausforderung, da die Stromwelle nicht dieselbe Frequenz wie Spannung oder Strom hat.

Außerdem bedeutet der Phasenwinkel für Leistung etwas ganz anderes als der Phasenwinkel für Spannung oder Strom. Während der Winkel für Spannung oder Strom eine relative Zeitverschiebung darstellt zwischen zwei Wellen stellt der Phasenwinkel für die Leistung ein Verhältnis . dar zwischen Verlustleistung und zurückgegebener Leistung.

Aufgrund dieser Art und Weise, in der sich Wechselstrom von Wechselspannung oder -strom unterscheidet, ist es tatsächlich einfacher, Zahlenwerte für die Leistung durch Berechnung mit Skalar zu erhalten Größen von Spannung, Strom, Widerstand und Reaktanz, als es ist, sie aus dem Vektor abzuleiten , oder komplex Größen von Spannung, Strom und Impedanz, mit denen wir bisher gearbeitet haben.

RÜCKBLICK:

• In einer rein ohmschen Schaltung wird die gesamte Schaltungsleistung durch den (die) Widerstand(e) abgeleitet. Spannung und Strom sind phasengleich.
• In einem reinen Blindstromkreis wird keine Stromkreisleistung durch die Last(en) verbraucht. Stattdessen wird Leistung abwechselnd von der Wechselstromquelle absorbiert und an diese zurückgegeben. Spannung und Strom sind um 90° phasenverschoben.
• In einer Schaltung bestehend aus gemischten Widerständen und Reaktanzen wird mehr Leistung von den Lasten verbraucht als zurückgegeben, aber ein Teil der Leistung wird definitiv verbraucht und ein anderer Teil wird nur absorbiert und zurückgegeben. Spannung und Strom in einem solchen Stromkreis sind um einen Wert zwischen 0° und 90° phasenverschoben.

VERWANDTES ARBEITSBLATT:

• Wechselstrom-Arbeitsblatt