Harmonische Phasenfolgen

Im letzten Abschnitt haben wir gesehen, wie die 3. Harmonische und alle ihre ganzzahligen Vielfachen (zusammen als Triple . bezeichnet) Harmonische), die durch 120° phasenverschobene Grundwellenformen erzeugt werden, sind tatsächlich in Phase miteinander.

In einem 60-Hz-Drehstromnetz, in dem die Phasen A , B , und C 120° voneinander entfernt sind, fallen die Vielfachen der dritten Harmonischen dieser Frequenzen (180 Hz) perfekt in Phase miteinander.

Dies kann man sich grafisch (Abbildung unten) und/oder mathematisch vorstellen:

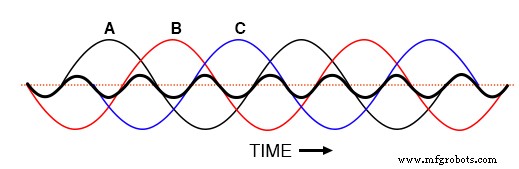
Harmonische Ströme der Phasen A, B, C fallen alle zusammen, dh keine Drehung.

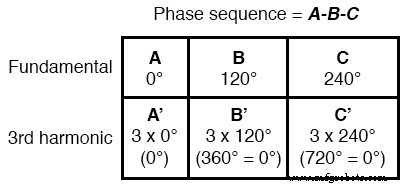
Erweiterte mathematische Tabelle mit ungeradzahligen Oberschwingungen

Wenn wir die mathematische Tabelle um höhere ungeradzahlige Harmonische erweitern, werden wir feststellen, dass sich ein interessantes Muster in Bezug auf die Rotation oder Reihenfolge der harmonischen Frequenzen entwickelt:

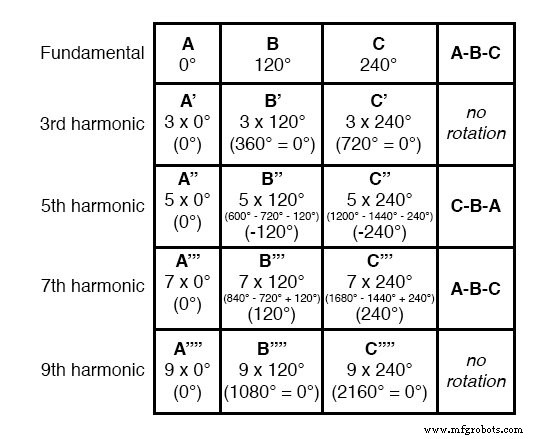
Harmonische wie die 7., die mit der gleichen Folge wie der Grundton „rotieren“, werden als positive Folge bezeichnet .

Harmonische wie die Quinte, die in der entgegengesetzten Reihenfolge wie der Grundton „rotieren“, werden als Negativsequenz bezeichnet .

Triplen-Harmonische (3. und 9. in dieser Tabelle gezeigt), die sich überhaupt nicht „drehen“, weil sie in Phase miteinander sind, werden als Nullfolge bezeichnet .

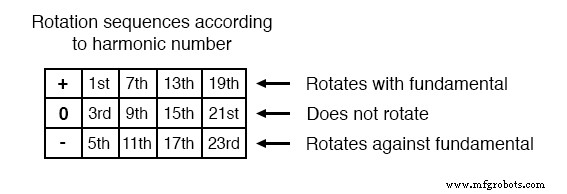
Dieses Muster von positiv-null-negativ-positiv setzt sich für alle ungeradzahligen Harmonischen unbegrenzt fort und eignet sich für den Ausdruck in einer Tabelle wie dieser:

VERWANDTE ARBEITSBLÄTTER:

• Arbeitsblatt für gemischtfrequente Signale