Gekoppelte resonanzverstärkte Modulation für einen Graphen-beladenen Metamaterial-Absorber

Hintergrund

Plasmonische Metamaterial (PM)-Absorber arbeiten mit metallischen Nanostrukturen im tiefen Subwellenlängenbereich. Perfekte Absorptionen können bei bestimmten Wellenlängen erreicht und angepasst werden, was zu einer Vielzahl von Anwendungen führt, einschließlich Lichtemitter/-detektor, Sensor, photothermische Therapie, optisch-mechanische Interaktion und hyperspektrale Bildgebung [1,2,3,4,5,6,7 ]. PM-Absorber bieten auch eine vielversprechende Plattform für die Entwicklung neuartiger funktioneller Bauelemente mit einstellbaren Eigenschaften. Durch die Einführung von Komponenten wie Flüssigkristallen, Halbleitern oder Phasenwechselmaterialien kann die optische Reaktion elektrisch, optisch oder thermisch moduliert werden [8,9,10,11,12,13], was neue Arten von Modulatoren, Schaltern ermöglicht , und multispektrale Detektoren.

In jüngster Zeit hat Graphen aufgrund seiner Hochgeschwindigkeits-Modulationsfähigkeit und -Abstimmbarkeit als plasmonisches Material beträchtliche Aufmerksamkeit erregt [14,15,16,17,18,19,20]. Insbesondere hängt die Graphenleitfähigkeit vom Fermi-Niveau (E _F ), die durch Vorspannung innerhalb von mehreren Nanosekunden kontinuierlich abgestimmt werden kann, was eine hohe Modulationsrate im nahen Infrarot und mittleren Infrarot ermöglicht [17, 19, 20, 21, 22, 23, 24]. Da die einzelne Graphenschicht jedoch nur atomar dick ist, ist die Wechselwirkung zwischen dem einfallenden Licht und der plasmonischen Resonanz recht schwach. Und diese Wechselwirkung wird im mittleren Infrarotbereich durch die Pauli-Blockierung von Interband-Übergängen noch schwächer [22]. Als Ergebnis ist der Wellenlängen-Abstimmbereich sowie die Modulationstiefe ziemlich begrenzt. Die Wellenlängenverschiebung beträgt im Allgemeinen weniger als 10 % der Resonanzwellenlänge [21, 22, 25, 26, 27, 28], was für praktische Anwendungen in der optischen Kommunikation und breitbandigen Spektraldetektionen immer noch eine Herausforderung darstellt. Um eine effiziente elektrooptische Modulation zu erreichen, muss die Graphen-Licht-Wechselwirkung daher stark verstärkt werden. In früheren Studien wurden einige Fortschritte erzielt. Basierend auf dem Design komplexer Nanostrukturen wie Nanoantennen und Split-Ring-Resonatoren [19, 21, 22, 25, 27, 28] wurde die Verstärkung der Graphen-Licht-Wechselwirkung theoretisch und experimentell nachgewiesen. Diese Konstruktionen sind jedoch in der Regel kompliziert oder polarisationsabhängig, der Arbeitsfrequenzbereich ist relativ klein und die Durchstimmbarkeit ist immer noch begrenzt.

In dieser Arbeit haben wir einen Graphen-beladenen Absorber mit einem Modulationsbereich von 9 bis 14 µm vorgeschlagen, der für Anwendungen wie biochemische Sensorik und thermische Bildgebung von großem Interesse ist [5, 29,30,31]. Die gekoppelten Resonanzen innerhalb des kreuzförmigen Schlitzes bieten vier Verstärkungsordnungen für das elektrische Feld, was die Graphen-Licht-Wechselwirkung stark verstärkt und zu einer Verschiebung der zentralen Wellenlänge von bis zu 25% führt. Darüber hinaus schlagen wir ein einfaches LC-Schaltungsmodell vor, das die durch die Spannung und geometrische Parameter gesteuerte Graphen-induzierte Modulation gut erklärt und vorhersagt. Ein so großer Einstellbereich wäre für viele Anwendungen vielversprechend.

Methoden

Wie in Fig. 1a gezeigt, werden gemusterte Metallflecken mit einer Periode von = 8 μm auf dem Metallsubstrat angeordnet, die durch einen dielektrischen Abstandshalter getrennt sind. Zwischen den Patches und dem Spacer liegt eine einzelne Graphenschicht. Das Substrat ist sehr dick und wirkt als Reflexionsspiegel. Die Dicke der Abstandsschicht beträgt t _d = 520 nm und die der metallischen Flecken ist t _m = 100 nm. Abbildung 1b zeigt die Draufsicht einer Elementarzelle. Zwei Untereinheiten sind diagonalsymmetrisch angeordnet, um die Polarisationsunabhängigkeit zu unterstützen. Auf jedem quadratischen Patch ist ein kreuzförmiger Schlitz eingeätzt, der ihn in vier kleine identische teilt. Die Größen der kleinen identischen in S ₁ und S ₂ sind l ₁ = 1.5 μm und l ₂ = 1,7 μm. Die Schlitzbreite für beide Untereinheiten beträgt a = 20 nm. Als metallisches Material wird in unserer Studie Gold (Au) gewählt, dessen optische Eigenschaft durch das Drude-Modell von \(\varepsilon\left(\omega\right)=1-{\omega}_p^2/\left . beschrieben wird (\omega \left(\omega +\tau\right)\right)\) mit ω _p = 1.369 × 10 ¹⁶ Hz und τ = 1.224 × 10 ¹⁴ Hz [32]. Der dielektrische Abstandshalter besteht aus Zinksulfid (ZnS), dessen optischer Index n . ist = 2.2 mit vernachlässigbarem Verlust im mittleren Infrarotbereich [33].

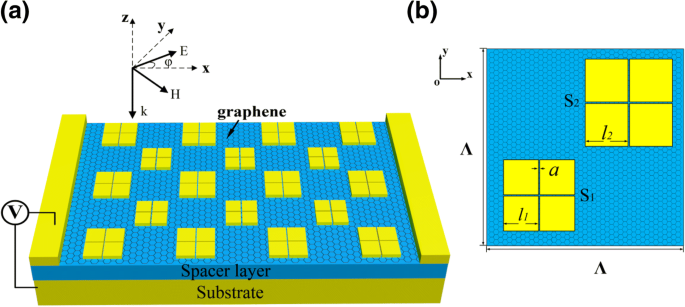
a Schematische Darstellung des vorgeschlagenen Graphen-beladenen Metamaterials. Der kreuzförmige Schlitz in jeder Untereinheit ermöglicht eine starke Verbesserung der Graphen-Licht-Wechselwirkung ohne Polarisationsabhängigkeit. b Draufsicht auf die Struktur in einem Zeitraum. Zwei Untereinheiten sind diagonal mit unterschiedlichen Patch-Größen angeordnet

Die Finite-Difference-Time-Domain-Methode (FDTD; Lumerical FDTD Solutions) wird verwendet, um Reflexionsspektren und elektromagnetische Feldverteilung zu berechnen. Die Simulationen erfolgen mit periodischen Randbedingungen im x und y Richtungen und perfekt angepasste Schichtbedingungen in der z Richtungen. Die einzelne Graphenschicht wird durch den Oberflächenleitfähigkeitsansatz als zweidimensionale Struktur modelliert [34]. Die Oberflächenleitfähigkeit der Graphenschicht σ _g , einschließlich des Interband-Terms σ _inter und der Intraband-Term σ _intra , kann mit der Kubo-Formel [35] berechnet werden.

wo e und ξ sind Ladung und Energie des Elektrons, ℏ ist die reduzierte Plankenkonstante, ω ist die Kreisfrequenz, \({f}_d\equiv 1/\left({e}^{\left(\xi -{E}_F\right)/{k}_BT}+1\right)\) bezieht sich zur Fermi-Dirac-Verteilung, T ist die absolute Temperatur, Γ ist die Streurate, k _B ist die Boltzmann-Konstante und E _F ist das Fermi-Niveau. In unserer Berechnung ist T = 300 K und Γ = 10 meV [28]. Die Maschenweite in der Nähe der Graphenschicht beträgt 0,25 nm und in den Schlitzen 2,5 nm. Die effektive Permittivität von Graphen kann dann ausgedrückt werden als

wo ε ₀ ist die Permittivität des Vakuums und t _g ist die Dicke der Graphenschicht. Gleichungen (1) und (2) zeigen, dass sich die optischen Konstanten von Graphen mit E . ändern _F . Diese Änderung führt zu einer Abstimmbarkeit der Absorptionsfrequenz, deren Bereich durch die gekoppelte Resonanz in den Nanostrukturen stark vergrößert werden kann, wodurch die angelegte Spannung in Geräten erheblich gesenkt wird.

Ergebnisse und Diskussion

Abbildung 2a zeigt die Absorptionsspektren für x -polarisierte Welle (φ = 0) bei senkrechtem Einfall. Wenn das Fermi-Niveau E ist _F = 0eV, bei der Wellenlänge λ . werden zwei Absorptionspeaks beobachtet = 12,4 μm bzw. 13,3 μm. Das einfallende Licht im Bereich von 12,1 bis 13,5 µm wird von der Nanostruktur fast absorbiert. Als E _F erhöht, bewegt sich die Resonanz in Richtung kürzerer Wellenlänge. Bei E _F = 0,2 eV, verschieben sich die Absorptionspeaks zu 11,8 μm und 12,46 μm, was eine relative Verschiebung von 4,8% bzw. 6% anzeigt. Unterdessen nimmt die Absorption von Peak 2 ab, was auf die Impedanzfehlanpassung zwischen dem Metamaterial und Luft bei einem höheren E . zurückgeführt wird _F [28]. Hier ist es interessant, dass sich Peak 2 schneller blau verschiebt als Peak 1, wenn das Fermi-Niveau weiter ansteigt. Dieses beobachtete Verhalten wird später durch ein Schaltungsmodell erklärt.

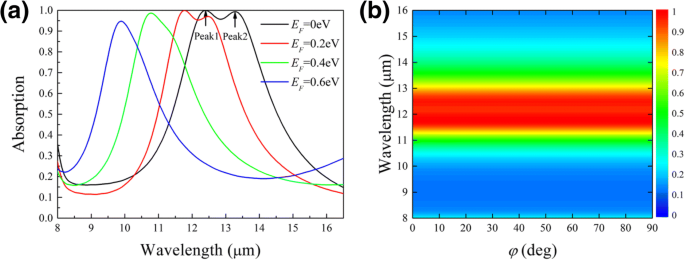
Absorptionsspektren bei senkrechtem Einfall mit verschiedenen E _F bei φ = 0, zeigt eine große Blauverschiebung der Peaks mit zunehmendem E _F (a ) und mit verschiedenen φ bei E _F = 0.2eV, was eine Polarisationsunabhängigkeit demonstriert (b ). Der Polarisationswinkel φ ist definiert wie in Abb. 1a

Die Modulation kann durch einen Parameter M . quantifiziert werden = Δλ /λ ₀ , wobei λ ₀ ist die Resonanzwellenlänge bei E _F = 0 eV und Δλ ist die Wellenlängenverschiebung aufgrund der Änderung von E _F . Abbildung 2a zeigt M ₁ = 20,1 % und M ₂ = 25,5% für Peak 1 bzw. Peak 2, wenn E _F erreicht 0,6 eV. Der Modulationsbereich von Resonanzen ist im Vergleich zu früheren Arbeiten viel breiter [19, 21, 22, 25, 26, 27, 28]. Eine so große Modulation bei einem niedrigen E _F ist für viele Anwendungen sehr wünschenswert. Separate Berechnungen zeigen, dass sich die Absorptionspeaks mit abnehmender Dicke des Spacers blau verschieben (Zusatzdatei 1). Somit können wir die Dicke optimieren, um einen geeigneten Startpunkt der Modulation festzulegen. Darüber hinaus ist die optische Reaktion des vorgeschlagenen Metamaterials polarisationsunabhängig, wie in Abb. 2b gezeigt. Das Absorptionsspektrum bleibt unverändert, wenn der Polarisationswinkel φ variiert aufgrund der Symmetrie des Designs von 0 bis 90°.

Der Mechanismus perfekter Absorptionen wird durch die Feldverteilungen an den Resonanzen deutlich veranschaulicht. Aufgrund der bekannten Metall-Isolator-Metall (MIM)-Struktur [3, 32, 36, 37, 38], die in Abb. 1 gezeigt ist, werden lokalisierte SPPs stimuliert, um in jedem Patch kompakte magnetische Resonanzen zu bilden. Abbildung 3a und b zeigen das normalisierte Magnetfeld |H| ² in der Graphenschicht für E _F = 0.2 eV bei den Resonanzwellenlängen von λ ₁ = 11,8 μm und λ ₂ = 12,46 μm. Da die SPPs stark lokalisiert sind, können zwei Untereinheiten unabhängig voneinander arbeiten. Aufgrund der geringen Breite des Teilungsschlitzes innerhalb jeder Untereinheit sind die Resonanzen der vier identischen Elemente jedoch tatsächlich miteinander gekoppelt. Und diese Kopplung erhöht das elektrische Feld innerhalb des Schlitzes enorm, wie in Abb. 3c und d gezeigt. Nur das E Felder im y -Richtungsschlitz sind hier offensichtlich, da das einfallende Licht im x liegt Polarisation. Die Intensität des E das durch die Resonanzkopplung verstärkte Feld ist vier Größenordnungen größer als das des einfallenden Lichts E _inc . Im Gegensatz dazu befinden sich die intensivsten Felder, die in früheren Arbeiten für die Modulation verwendet wurden, an den Patch-Rändern. Abbildung 3e und f zeigen den scharfen Vergleich der Verbesserungen zwischen den Schlitzen und Kanten entlang der weißen Linie in Abbildung 3c bzw. d.

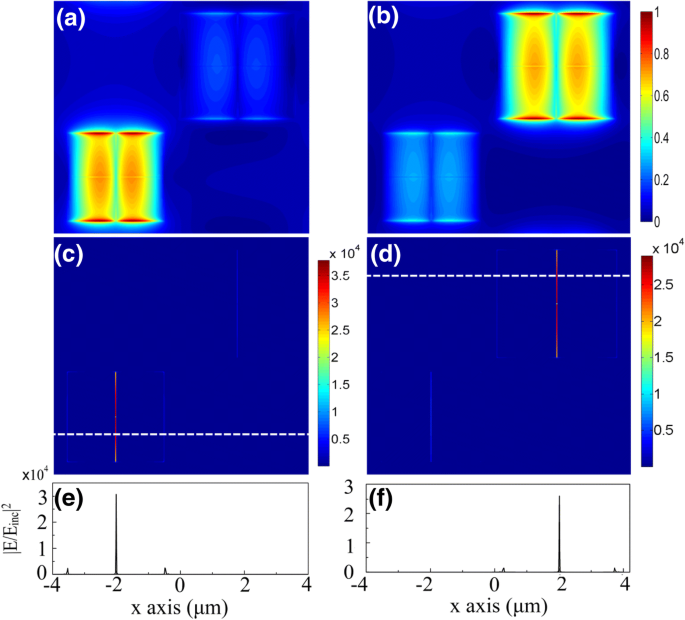
Feldverteilungen in der Graphenschicht bei E _F =0,2 eV für das x-polarisierte Licht bei senkrechtem Einfall, was eine starke Verstärkung im Schlitz zeigt, die durch die gekoppelten Resonanzen verursacht wird. a, b Normalisiertes Magnetfeld |H| ² bei λ ₁ = 11,8 μm (a ) und λ ₂ = 12.46 μm (b ); c , d Die entsprechende Feldverteilung von |E/E_inc | ² ; e , f |E/E_inc | ² entlang der weißen Strichlinie in c und d , bzw. Es ist ein scharfer Kontrast zwischen der Intensität innerhalb des Schlitzes und der an den Kanten des Patches zu sehen, was Hinweise auf einen viel größeren Stimmbereich als in früheren Werken gibt

Solche Feldverteilungen erklären gut den Grund, warum die Modulation in unserem Vorschlag so groß ist. Basierend auf einer Störungstheorie kann die Graphen-induzierte Resonanzverschiebung als Δω . bewertet werden =  − iσ _g ∫_S |E_s | ² dS /W ₀ [22]. Hier, |E_s | ² ist die Intensität des elektrischen Felds in der Graphenschicht, W ₀ ist die gespeicherte Energie und S bezeichnet die vom Graphen bedeckte Fläche. Die spektrale Verschiebung der Resonanz (Re(Δω )) wird durch den Imaginärteil von σ . entschieden _g , der viel größer ist als sein realer Anteil im mittleren Infrarotbereich [22, 28]. Wie in den Abb. 3c–f deutlich zu sehen ist, ist die Verstärkung des elektrischen Feldes innerhalb des schmalen Schlitzes mehr als das Zehnfache derjenigen an den Rändern. Als Ergebnis wird der Integralwert hauptsächlich durch das stark verbesserte E . beigesteuert Feld in den Patch-Slots, was zu einer viel größeren Verschiebung der Peaks führt als in früheren Fällen, die nur das verbesserte E . besitzen Felder an den metallischen Kanten [21, 22, 25, 27, 28].

Entsprechend den Feldverteilungen und den obigen Diskussionen wird ein LC-Schaltungsmodell vorgeschlagen, um das Abstimmverhalten zu untersuchen. Wie in Abb. 4a gezeigt, L _ich und C _ich (ich = 1, 2) sind die Induktivität bzw. die Kapazität für das Patch S _ich in Abb. 1b. Wenn die Schlitzbreite a sehr groß ist und es keine Graphenschicht gibt, können wir die durch die Schlitze und Graphen induzierten Effekte ignorieren. Dann, L _ich und C _ich kann durch separate Berechnungen durch Anpassung an die in Absorptionsspektren erhaltene Resonanzwellenlänge entschieden werden [37, 39, 40]. Die Ergebnisse sind L ₁ = 0.07 pH und C ₁ = 350 aF für Untereinheit S ₁ , während L ₂ = 0.075 pH und C ₂ = 380 aF für Untereinheit S ₂ . Der schlitzinduzierte Kopplungseffekt innerhalb jeder Untereinheit kann durch eine Shunt-Kapazität C . beschrieben werden _c , die mit zunehmender Schlitzbreite kleiner wird a . In unseren Fällen C _c ist 290 aF für a = 20 nm und wird 200 aF, 180 aF und 135 aF mit jedem zunehmenden 10 nm von a . Die Resonanzwellenlänge erhält man, indem man die Impedanz des Schaltkreises gleich null lässt, dh \( {\lambda}_i^0=2\pi {c}_0\sqrt{L_i{\mathrm{C}}_i^0} \). Hier, c ₀ ist die Lichtgeschwindigkeit im Vakuum, „i ” bezieht sich auf die Untereinheit S _ich , und \( {C}_i^0={C}_i+{C}_c \).

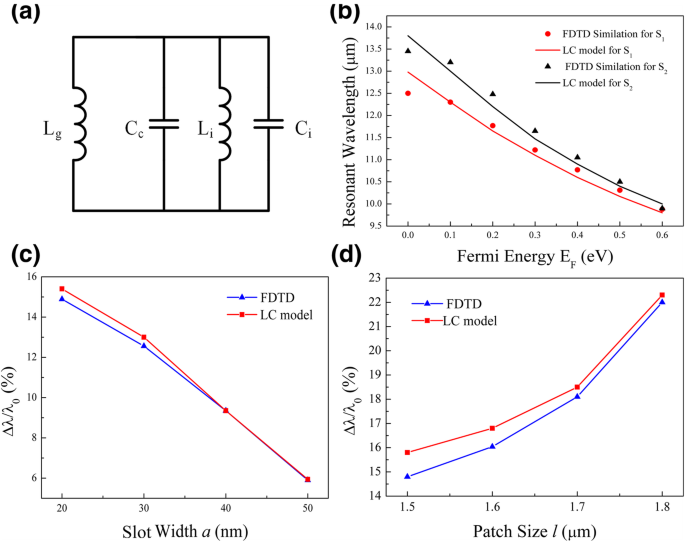
a Ein LC-Schaltungsmodell enthält Beiträge von separaten Patches (L _ich und C _ich ), Steckplatz (C _c ) und Graphen (L _g ). b Vom LC-Modell berechnete Resonanzen im Vergleich zu FDTD-Simulationen. c , d Resonanzverschiebung für einen einzelnen Patch bei E _F = 0.4 eV mit sich änderndem geometrischen Parameter von c Schlitzbreite (l = 1,5 μm) und d Patchgröße (a = 20 nm)

Die zweidimensionale Graphenschicht fungiert im Wesentlichen als Induktor. Wie in Abb. 3 gezeigt, kommt der Hauptbeitrag der Graphenschicht von der Schlitzposition, an der das elektrische Feld verstärkt wird. Da die Schlitzbreite viel kleiner ist als die Betriebswellenlänge und die Wellenlänge des Graphenplasmons, ist die quasistatische Näherung gültig. Die Spannung V und das aktuelle Ich über den Schlitz kann mit V . ausgewertet werden = aE undich = 2l _ich t _g (σ _g − iωε ₀ )E , wobei E ist das elektrische Feld in der Graphenschicht. Wir können also eine Induktivität L . einführen _g =  − 1/ω Im(V/I) [41], das den Beitrag der Graphenschicht beschreibt und als

Dieser Induktor dient als paralleles Element, das in Fig. 4a gezeigt ist. Als Ergebnis erhält man die Gesamtinduktivität eines Patches zu \( 1/{L}_i^{\prime}=1/{L}_i+1/{L}_{\mathrm{g}}\). Die endgültige Resonanzwellenlänge jeder Untereinheit mit der Graphenschicht wird

Da jede Untereinheit unabhängig arbeitet, kann die Gesamtimpedanz des Metamaterials aus der Parallelschaltung der Impedanzen der beiden Untereinheiten erhalten werden.

Dieses LC-Modell sagt eine Blauverschiebung der Resonanz mit zunehmendem E . voraus _F . Abgeleitet aus Gl. (1) und (2) erhalten wir einen größeren Wert von |Re(ε _g )| für das Graphen bei einem höheren E _F , was ein kleineres L ergibt _g in Gl. (3). Durch die Parallelschaltung der Induktivitäten wird die Endinduktivität \({L}_i^{\prime}\) kleiner, was zu einer kürzeren Resonanzwellenlänge in Gl. (4). Das berechnete Ergebnis ist in 4b zusammengefasst und zeigt eine gute Übereinstimmung mit der Resonanzwellenlänge, die durch die FDTD-Simulationen erhalten wurde. Eine kleine Abweichung ist zu sehen, weil unser LC-Modell den Beitrag schwacher Felder an den Rändern jedes Patches ignoriert (Abb. 3c–f). Das LC-Modell zeigt auch, wie die geometrischen Parameter die Blauverschiebung der Resonanz beeinflussen. Ableitung von Gl. (4), wir haben \(\partial{\lambda}_i^{\prime}/\partial{L}_i^{\prime}\propto 1/\sqrt{L_i^{\prime}}\). Es ist offensichtlich, dass ein kleiner Wert von \(\sqrt{L_i^{\prime}}\) bevorzugt wird, um die Empfindlichkeit dieser Blauverschiebung zu erhöhen. Da die Induktivitäten parallel geschaltet sind und L _ich fest ist, bedeutet ein kleiner Wert der Gesamtinduktivität \( {L}_i^{\prime } \) einen kleinen Wert der Grapheninduktivität L _g . Um den Stimmbereich zu erhöhen, muss die Schlitzbreite a sollte klein sein und die Patchgröße l groß sein, nach Gl. (3). Abbildung 4c zeigt, dass die Blauverschiebung der Resonanz bei E _F = 0.4 eV steigt von etwa 6 auf 15%, wenn die Schlitzbreite innerhalb von S ₁ von 50 auf 20 nm abnimmt. Auf der anderen Seite, wenn wir die Schlitzbreite auf a =20 nm, die Resonanz steigt von 15 auf 22% mit einer Änderung der Patchgröße von 1,5 auf 1,8 μm, wie in Fig. 4d gezeigt. Die gute Übereinstimmung mit den FDTD-Simulationen zeigt, dass ein so einfaches Schaltungsmodell eine effiziente Methode zum Studium verwandter Metamaterialbauteile ist.

Schlussfolgerungen

Zusammenfassend haben wir einen polarisationsunabhängigen, breitbandigen Metamaterial-Absorber mit einem großen Modulationsbereich entwickelt. Für beide Resonanzen erreicht der Abstimmbereich bis zu 20,1 % und 25,5% der zentralen Wellenlänge, wenn E _F steigt von 0 auf 0,6 eV. Eine solch große Modulation kommt von der Graphen-Licht-Wechselwirkung, die durch die gekoppelten Resonanzen innerhalb des kreuzförmigen Schlitzes jedes Metallflecks enorm verstärkt wird. Dieser Effekt wird durch einen Graphen-eingeführten Induktor im LC-Modell gut beschrieben. Ein so einfaches Modell sagt das Modulationsverhalten unter verschiedenen geometrischen Parametern voraus, und die Ergebnisse stimmen gut mit den FDTD-Simulationen überein. Unser Vorschlag ist für potenzielle Anwendungen wie optische Kommunikation, Sensorik und Wärmebildgebung von Vorteil.

Abkürzungen

E _F :

Fermi-Niveau

FDTD:

Endlich-unterschiedliche Zeitdomäne

MIM:

Metall-Isolator-Metall

PM:

Plasmonisches Metamaterial

ZnS:

Zinksulfid