Plasmonisch induzierte perfekte Absorption im Graphen/Metall-System

Hintergrund

Plasmonik hat aufgrund ihrer außergewöhnlichen Eigenschaften [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15] und ihres enormen Potenzials in vielen Bereichen, einschließlich integrierter Photonik, Biosensorik, Energieerfassung, Photodetektion. Vor kurzem wurde ein neuartiges plasmonisches Phänomen beobachtet, das als Spoof-Oberflächenplasmonen (SSPs) bekannt ist und sich durch perforierte Metalle ausbreiten und die Beugungsgrenze überwinden kann [16]. SSPs wurden dann im THz-, Mikrowellen- und unteren Frequenzbereich untersucht [17,18,19] und eine Reihe von Geräten mit tiefen Subwellenlängen basierend auf SSPs wurde vorgeschlagen [20, 21]. Die Anwendung solcher Geräte wird jedoch durch die hohe Dämpfungsrate von SPPs ernsthaft behindert. Eine Lösung für dieses Problem ist das Medium künstlicher Plasmonen-induzierter Transparenz (PIT) [22], das ein scharfes Transparenzfenster innerhalb eines breiten Absorptionsspektrums aufweist. Der PIT-Effekt beruht hauptsächlich auf der Kopplung eines strahlenden Elements und eines unterstrahlenden Elements, was umfassend untersucht wurde [23,24,25]. Ein ähnliches Phänomen, die plasmoneninduzierte Absorption (PIA), wurde kürzlich auch gezeigt, die aus der konstruktiven Interferenz heller und dunkler plasmonischer Moden resultiert [26]. Die PIA-Resonanz [27, 28] kann einen bemerkenswert schnellen Lichteffekt aufweisen, der potenzielle Anwendungen beim optischen Schalten und Verarbeiten hat.

Herkömmliche Vorrichtungen, die auf dem PIA-Effekt der Metallstruktur basieren, sind jedoch nur schwer oder gar nicht abstimmbar, was ihre Anwendungen stark einschränkt. Graphen [29, 30], das für seine Halbmetallizität, hohe Mobilität und hohe Abstimmbarkeit bekannt ist, kann ein hervorragender Materialkandidat für abstimmbare plasmonische Infrarotgeräte sein. In diesem Artikel untersuchten wir einen abstimmbaren PIA-Effekt, der durch die konstruktive Interferenz einer F-P-Resonanzmode und einer quasi-geführten Mode, unterstützt durch eine periodische Silberrille bzw. Monolayer-Graphen, erreicht wird. Es zeigt sich, dass Resonanzstärke und Linienbreite stark vom Kopplungsabstand abhängen. Es wird auch gezeigt, dass das Extinktionsverhältnis ~ 99,999 % erreichen kann. Das Extinktionsverhältnis ist definiert als 1-R -T , wobei R und T sind das Reflexionsvermögen bzw. das Transmissionsvermögen. Es ist einfach 1-R in unserem System, da die Transmission hier 0 ist. Als Ergebnis ist ein ultrahohes FOM* von bis zu 10 ⁶ im Graphen/Metall-System erreicht werden und die Resonanzfrequenz kann durch Einstellen der Gatespannung von Graphen dynamisch abgestimmt werden. Diese herausragenden Eigenschaften können in biochemischer Sensorik und dynamischem optischem Schalten angewendet werden.

Methoden

Das Schema unserer Struktur ist in Abb. 1 dargestellt, bestehend aus einem Monolayer-Graphen und einem Al₂ O₃ isolierte Schicht auf einem gerillten Silber. Die Dicke des Al₂ O₃ ist g . Das System wird durch eine normal einfallende ebene Welle mit transversaler magnetischer (TM) Polarisation beleuchtet. Die anderen Strukturparameter werden wie folgt ausgedrückt:d ist die Tiefe der Silberrille; w ist die Breite der Silberrille; P ist die Periode der Elementarzelle. Im mittleren Infrarotbereich dominiert die Intraband-Streuung in hochdotiertem Graphen, und seine Leitfähigkeit nimmt eine Drude-ähnliche Form an σ _g =dh ² E _F /[πħ ² (ω +iτ ^-1 )]. Die Elektronenrelaxationszeit wird als τ . ausgedrückt =μE _F /eυ _F ² , wobei υ _F =c /300 ist die Fermi-Geschwindigkeit, E _F ist die Fermi-Energie und μ =10 m ² /Vs ist die Gleichstrommobilität von Graphen [25, 31, 32]. In den Finite-Difference-Time-Domain-Simulationen (FDTD) werden die optischen Konstanten für Silber und Al₂ O₃ sind aus ref. [33] und Lit. [34]. Die periodischen Randbedingungen werden verwendet, um unendlich periodische Zellstrukturen zu simulieren. Der Einfachheit halber nehmen wir an, dass das Material der Region über der Graphenschicht Vakuum ist (ε ₀ =1).

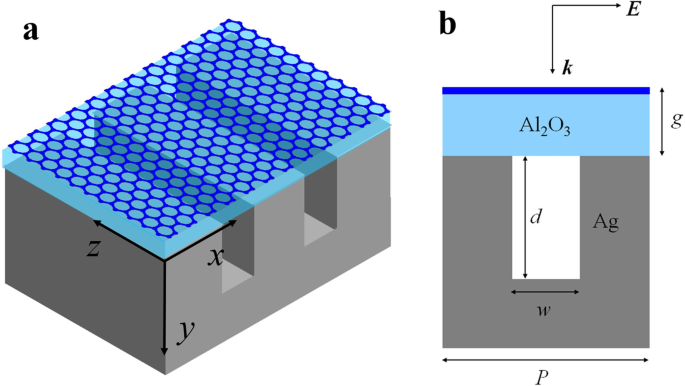
Schematische Darstellung der Graphen-Silber-Rillenstruktur. a Schrägansicht. b Das Querschnittsdiagramm einer Elementarzelle

Ergebnisse und Diskussion

Wir haben das Reflexionsspektrum der Silberrille mit w . simuliert =100 nm, P =250 nm, d =2000 nm, und das Ergebnis ist in Abb. 2a (rote Kurve) dargestellt. Ein breiter Einbruch ist bei ~ 28 THz zu beobachten, mit einem Extinktionsverhältnis von ~ 44% und Q Faktor ~ 0.8, was auf eine F-P-Resonanz zurückzuführen ist, die durch die durch einfallendes Licht angeregte SSP induziert wird [19]. Diese Resonanz hat einen weiten Bereich von Resonanzbändern und somit kann die Resonanzmode als Superradiant Mode in unserem PIA-System dienen. Dann berechneten wir das Reflexionsspektrum des Graphenblechs mit Metallrandbedingungen im unteren Bereich des Simulationsbereichs mit einem Fermi-Niveau E _F =0,3 eV, wie in Abb. 2a (blaue Kurve) dargestellt. Das Reflexionsspektrum zeigt, dass die Graphen-Plasmonenresonanz durch den Einfall bei dieser Frequenz nicht direkt angeregt werden kann. Um die vom Graphen unterstützte Plasmonenmode zu visualisieren und zu optimieren, simulieren wir zunächst die vom Graphen unterstützten Resonanzmoden. Um die potenziellen Auswirkungen der F-P-Resonanz der Silberrille zu eliminieren, gehen wir davon aus, dass die Rille aus Silizium statt aus Silber besteht. Die Reflexionsspektren der Struktur wurden für E . berechnet _F =0,3 eV und verschiedene Elementarzellen P und ist in Fig. 2b gezeigt. Ein Reflexionsabfall bei der Resonanzfrequenz f =32,84 THz kann für P . beobachtet werden =250 nm mit einem Q Faktor ~ 304. Das hohe Q Resonanz mit einem schmalen Resonanzband kann in unserem PIA-System als subradianter (dunkler) Modus dienen. Der Reflexionsabfall ist auf die Resonanz der plasmonischen quasi-geführten Mode in Graphen mit dem senkrechten Einfall zurückzuführen [35], da die Rille die Wellenvektorfehlanpassung basierend auf dem m . kompensieren kann Phasenanpassungsbedingung zweiter Ordnung [36, 37]

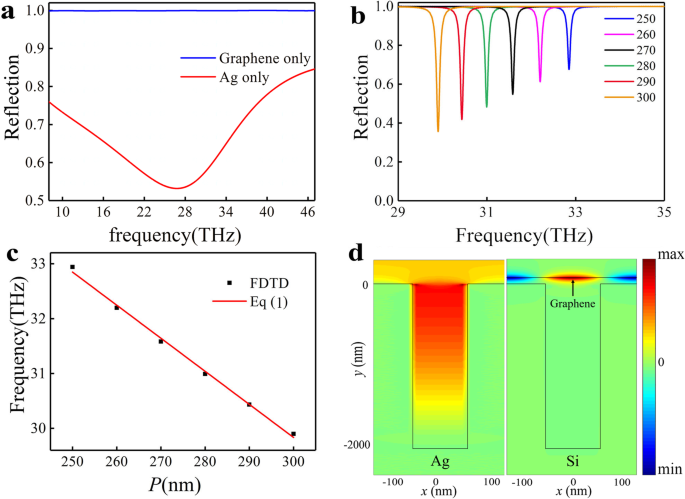
Optisches Verhalten der einzelnen Moden. a Die Reflexionsspektren der Struktur nur von Silberrillen (rote Linie) und nur von Graphen (blaue Linie) bei senkrechtem Einfall. b Die Reflexionsspektren der Struktur der Graphen-Si-Grabe für verschiedene Perioden P der Elementarzelle. c Die numerische Modellierung und analytische Ergebnisse der Resonanzfrequenz f , bzw. d Das elektrische Feld E _x Verteilungen des F-P-Modus (links) und des quasi-geführten Graphen-Resonanzmodus (rechts).

wo k _x =k ₀ Sündeθ , k ₀ =2π /λ ist der Wellenvektor im freien Raum, θ ist der Winkel zwischen dem einfallenden Licht und y -Richtung, n _eff der effektive Brechungsindex des TM-Wellenleitermodus im Graphen ist und G _x ist der reziproke Gittervektor des Gitters (G _x =2π /P ). In der folgenden Diskussion wird der Lichteinfallswinkel von y -Richtung ist null (θ =0°). Die Situation für andere Einfallswinkel wird in Zusatzdatei 1 diskutiert. Die Positionen dieser Reflektanzeinbrüche entsprechen der Resonanzfrequenz der quasi-geführten Mode im Graphen, wie in Abb. 2b gezeigt. Die Simulationsergebnisse stimmen gut mit der Gl. (1), wobei m =1 und der effektive Brechungsindex ~ 33 wird durch FDTD-Lösungen erhalten, wie in Fig. 2c gezeigt. Das elektrische Feld E _x Verteilungen des F-P-Modus und des quasi-geführten Graphen-Modus sind in Fig. 2d gezeigt. Es sei darauf hingewiesen, dass die Energieeinschränkung der SSP-Moden, die von der Si-gerillten Oberfläche aufrechterhalten werden, im Vergleich zu der quasi-geführten Mode von Graphen vernachlässigbar sein kann.

In der Kopplungssituation werden die beiden Eigenmoden stark gekoppelt, wenn sie sich einander nähern, und daher wird das Reflexionsspektrum dramatisch verändert. Ein schmaler Einbruch der Sublinienbreite mit erhöhter Absorption mit einem Extinktionsverhältnis von ~~99,97% wird über dem breiteren Einbruch des Reflexionsvermögens beobachtet, wie in Fig. 3a gezeigt. Beim Erhöhen des vertikalen Abstands g , die Nahfeldkopplung und die quasi-geführte Mode werden schwächer, wenn die Modulation des Reflexionsabfalls kleiner wird. Es gibt zwei Möglichkeiten, die dazu führen, dass der Reflexionsgradeinbruch kleiner wird, nämlich die schwächere Kopplung und die schwächere quasi-geführte Modenanregung. Daher haben wir das gekoppelte Oszillatormodell verwendet, um das PIA-System quantitativ zu verstehen [38].

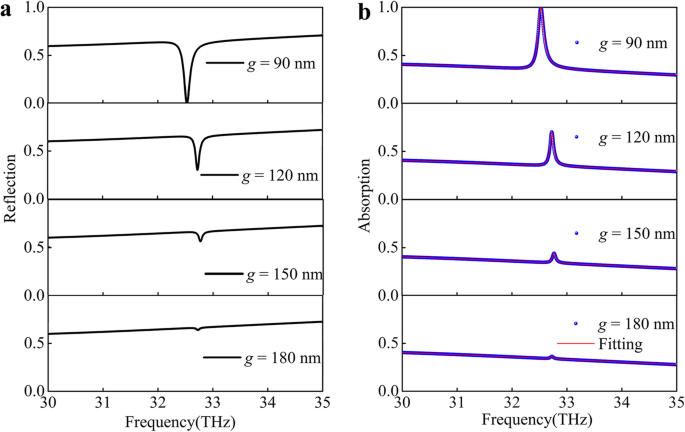
Die optische Reaktion variiert mit dem Kopplungsabstand. a Die Reflektion. b Absorptionsspektren der Struktur der Graphen-Silberfurche bei senkrechtem Einfall für unterschiedlichen Abstand g zwischen dem Graphen und der Silberrille. Die schwarze Kurve/die blauen Kugeln werden nach der FDTD-Methode berechnet und die rote Kurve wird nach Gl. (3) des PIA-Geräts

Wobei \({\tilde{a}}_{1,2}={a}_{1,2}\left(\omega \right){\textrm{e}}^{i\omega t}\) , ω _1,2 und γ _1,2 sind die zeitharmonischen Amplituden, Resonanzfrequenzen und Dämpfungskonstanten des Hellmodus bzw. des Dunkelmodus. b ist der Kopplungskoeffizient, der misst, wie stark die helle Mode mit dem einfallenden elektrischen Feld koppelt. \(\tilde{\kappa}=\kappa{e}^{i\varphi}\) ist ein komplexer Kopplungsparameter, der eingeführt wird, um den Phasenverzögerungseffekt auszudrücken. φ ist eine Phasenverschiebung, die ein Schlüsselkoeffizient ist, um die Form der Interferenz zwischen den beiden kohärenten Pfaden zu bestimmen. Wenn φ =0 ist ein reeller Parameter und das typische Verhalten des PIT-Effekts kann beobachtet werden, und die Interferenz zwischen den beiden kohärenten Pfaden ist destruktiv. Für φ =π/2 ist ein rein imaginärer Parameter und die Interferenz zwischen den beiden kohärenten Pfaden wird von destruktiv in konstruktiv umgewandelt [26]. Die Absorption des Systems kann als dissipierte Energie auf der Grundlage der Formel (2) berechnet werden, die

Dann passen wir die numerischen Absorptionsspektren mit der Gl. (3) für verschiedene g , die in Abb. 3b (rote Kurven) dargestellt sind. Die Simulationsergebnisse stimmen gut mit den analytischen Modellierungsergebnissen auf Basis des gekoppelten Oszillatormodells überein, was das Konstruktionsprinzip unseres PIA-Geräts stark bestätigt. Die Anpassungsparameter κ , φ , γ ₁ , und γ ₂ sind in Abb. 4a–c dargestellt. Die steigenden g ergibt eine Abnahme des Kopplungsparameters κ , wie in Fig. 4a gezeigt. Bei allmählicher Verringerung der Kopplung (Erhöhung von g ), die Phase φ ist unverändert und γ ₂ nimmt allmählich ab, während γ ₁ Änderungen leicht gezeigt in Abb. 4b, c. Der Kopplungsparameter κ überschreiten die Dämpfungskonstanten des Dunkelmodus γ ₂ für den minimalen Spaltabstand, was bestätigt, dass die Kopplung vom hellen Modus in den dunklen Modus stärker ist als die Dissipationsprozesse im Graphenblatt.

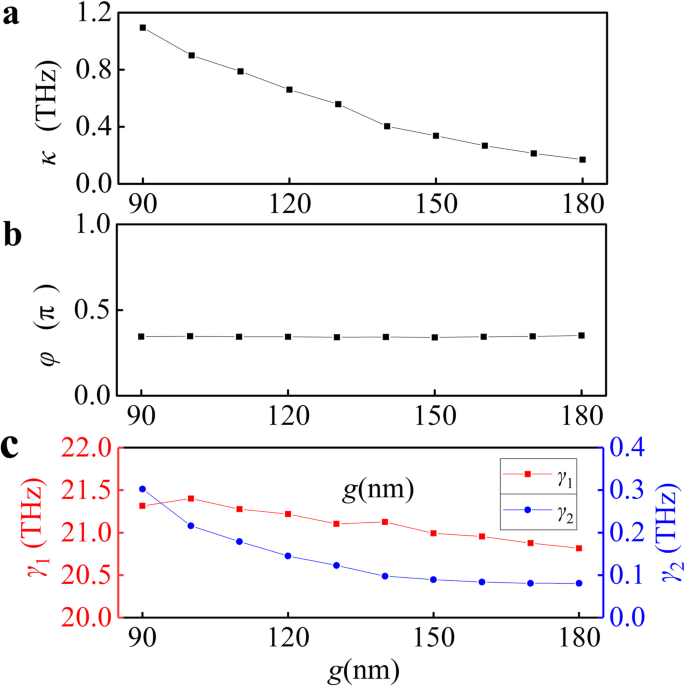
Quantitative Analyse optischer Reaktionen in gekoppelten Systemen. Extrahierte numerische (a ) Kupplung, (b ) Phase und (c ) Dämpfungskoeffizienten als Funktion der Lücke g . Werte von κ , φ , und γ ₁ , γ ₂ wurden durch Anpassen der numerischen Absorptionsspektren extrahiert

Um die konstruktive Interferenz zwischen den hellen und dunklen Moden zu visualisieren, untersuchten wir die Entwicklung des Magnetfelds der Struktur mit der Zeit und zwei H _z Monitore wurden 3 nm vom Zentrum des Graphens bzw. 1000 nm vom Boden der Silberrille entfernt platziert. Die oszillierende Phasendifferenz zwischen den beiden Moden beträgt 0,5 , wie in Fig. 5a angegeben. Die Magnetfeldverteilung zu einem anderen Zeitpunkt wurde in der PIA-Resonanzfrequenz f . berechnet _q =32,5 THz, wobei ω _q t ₁ ~ 2,00  und ω _q t ₂ ~ 2,50π, wie in Abb. 5b, c. Das Maximum des Magnetfelds in der Silberrille kann bei 2.00π beobachtet werden, während das Magnetfeld in Graphen sein Maximum bei 2.50π erreicht, was auf die phasenverschobene Kopplung zwischen den beiden Strukturen hinweist. Daher werden die Entwicklung und Bildung der Resonanz durch konstruktive Interferenz bestimmt [39].

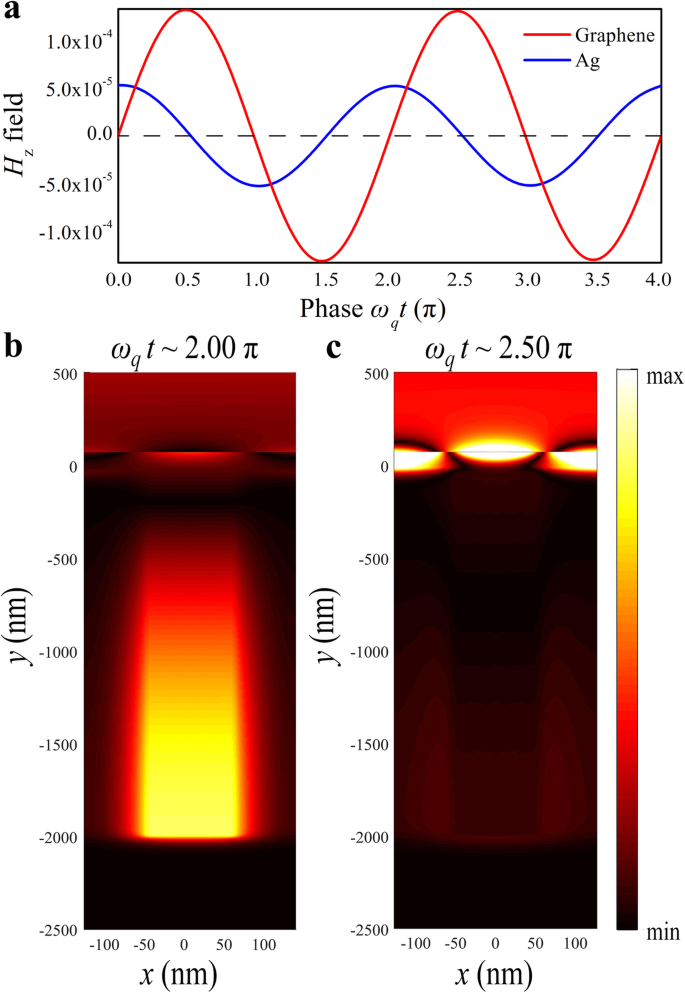
Zeitbereichsentwicklung gekoppelter Moden. a Berechnete zeitliche Entwicklung der magnetischen Feldstärke an Graphen (rote Linie) und Silberrille (blaue Linie). Berechnete z Komponente der Magnetfeldverteilungen für g =90 nm. Die maximale Feldstärke an Silberrille und Graphen wird zu unterschiedlichen Zeiten beobachtet b ω _q t ₁ ~ 2,00π und c ω _q t ₂ ~ 2,50π bzw.

In der praktischen Anwendung sind ein schmales Reflexionsband und ein hohes Extinktionsverhältnis sehr erwünscht. Um diese beiden Bedingungen zu erreichen, können wir den Zeitraum der Einheit P . anpassen und Tiefe der Silberrille d um unsere strukturellen Parameter zu optimieren. Nach Berechnung des Reflexionsspektrums verschiedener Strukturparameter P von 1900 bis 2100 nm und d von 245 bis 265 nm durch FDTD erreichen wir ein sehr hohes Extinktionsverhältnis von ~ 99,999 % in P =254 nm und d =1980 nm. Das Reflexionsspektrum der PIA-Vorrichtung unter verschiedenen Brechungsindexumgebungen ist in Fig. 6a gezeigt. Die Erfassungsfähigkeiten sind definiert als [39]:

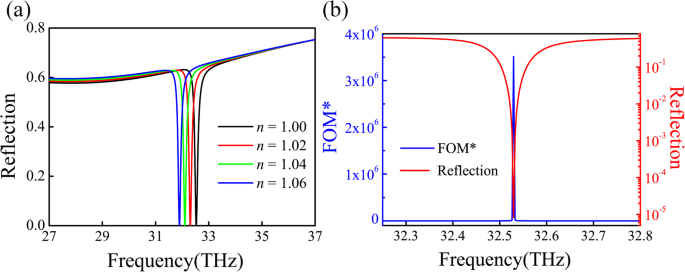
Die Erfassungsleistung des Systems. a Die Erfassungsantwort des PIA-Sensors für unterschiedliche dielektrische Umgebungen. b Die zugehörige FOM*-Kurve und die Reflexionsspektren

wo f und ich sind die Resonanzfrequenz bzw. die spektrale Intensität. Bei der Messung der Reflexionsintensität eines Sensors kann die Empfindlichkeit des Sensors durch den FOM*-Wert quantifiziert werden. Je höher der Wert, desto höher die Empfindlichkeit des Sensors. Aus Abb. 6 a erhalten wir S =11,2 THz/RIU und das zugehörige FOM ~ 94,1 mit der vollen Halbwertsbreite (FWHM) ~ 30 nm (0,12 THz). Dieser FOM ist größer als der Wert in Metamaterial-Absorbern basierend auf der Oberflächengitterresonanz. Außerdem kann unser PIA-Sensor zu einem ultrahohen FOM*-Wert von 3,5 × 10 ⁶ . führen , wie in Fig. 6b angegeben. Wir haben die Leistung der kürzlich untersuchten Sensoren in Zusatzdatei 1:Tabelle S1 verglichen.

Im PIA-System spielt Graphen eine weitere Schlüsselrolle. Die Modulation der Resonanzfrequenz kann durch Abstimmung der Gate-Spannung erreicht werden, um das Fermi-Niveau von Graphen einzustellen. Die simulierten Spektren sind in den Zusatzdateien 2:Abbildung S1 und 3:Abbildung S2 dargestellt. Die frequenzverschiebende aktive Steuerung der PIA-Resonanz ist für Sensor oder Absorber sinnvoll.

Schlussfolgerungen

Zusammenfassend haben wir die perfekte Absorption numerisch demonstriert, die durch konstruktive Interferenz zwischen der F-P-Resonanzmode und der plasmonischen quasi-geführten Graphenmode induziert wird. Durch die Einführung der plasmonischen quasi-geführten Mode von Graphen erhalten wir die Spektrallinie mit einer schmaleren Linienbreite der Silberrillen-F-P-Resonanzmode. Wenn der Abstand g allmählich erhöht wird, nehmen Resonanzstärke und Linienbreite ab. Für die Anwendung kann das FOM* in unserem System 10 ⁶ . erreichen . Darüber hinaus kann das Absorptionsfenster durch Variation der geometrischen Parameter und des Graphen-Fermi-Niveaus eingestellt werden. Diese Ergebnisse könnten einen neuen Weg zur Realisierung einer dynamischen Spektralsteuerung im mittleren Infrarot im Nanobereich und ultraempfindlicher optischer Sensoren eröffnen.

Verfügbarkeit von Daten und Materialien

Alle während dieser Studie generierten oder analysierten Daten sind in diesem veröffentlichten Artikel [und seinen ergänzenden Informationsdateien] enthalten.

Abkürzungen

FDTD:

Zeitbereich mit endlicher Differenz

FOM*:

Verdienstzeichen*

F-P:

Fabry-Perot

FWHM:

Volle Breite auf halbem Maximum

PIA:

Plasmon-induzierte Absorption

PIT:

Plasmoneninduzierte Transparenz

Q Faktor:

Qualitätsfaktor

SSPs:

Oberflächenplasmonen gefälscht

TM:

Quermagnetisch