Weitere Informationen zur Spektrumanalyse

Computergestützte Fourier-Analyse, insbesondere in Form der FFT Algorithmus, ist ein leistungsstarkes Werkzeug, um unser Verständnis von Wellenformen und ihren zugehörigen Spektralkomponenten zu verbessern.

Dieselbe mathematische Routine, die in den SPICE-Simulator wie die .fourier-Option einprogrammiert ist, wird auch in eine Vielzahl von elektronischen Testinstrumenten programmiert, um eine Echtzeit-Fourier-Analyse der gemessenen Signale durchzuführen.

Dieser Abschnitt widmet sich der Verwendung solcher Tools und der Analyse verschiedener Wellenformen.

Zuerst haben wir eine einfache Sinuswelle mit einer Frequenz von 523,25 Hz. Dieser spezielle Frequenzwert ist eine „C“-Tonhöhe auf einer Klaviertastatur, eine Oktave über dem „mittleren C“.

Tatsächlich wurde das für diese Demonstration gemessene Signal von einem elektronischen Keyboard erzeugt, das den Ton einer Panflöte erzeugte, der nächsten Instrumenten-„Stimme“, die ich finden konnte, die einer perfekten Sinuswelle ähnelt. Das folgende Diagramm wurde einer Oszilloskopanzeige entnommen und zeigt die Signalamplitude (Spannung) über die Zeit:

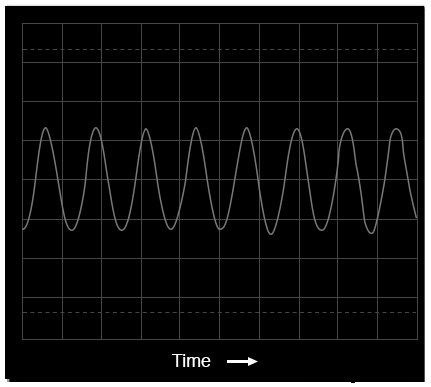
Oszilloskopanzeige:Spannung vs. Zeit

Mit einem Oszilloskop betrachtet, sieht eine Sinuswelle wie eine wellenförmige Kurve aus, die horizontal auf dem Bildschirm gezeichnet wird. Die horizontale Achse dieser Oszilloskop-Anzeige ist mit dem Wort „Time“ und einem in Richtung des Zeitverlaufs weisenden Pfeil gekennzeichnet. Die Kurve selbst stellt natürlich den zyklischen Anstieg und Abfall der Spannung im Laufe der Zeit dar.

Eine genaue Beobachtung zeigt Unvollkommenheiten in der Sinuswellenform. Dies ist leider auf die spezielle Ausrüstung zurückzuführen, die zur Analyse der Wellenform verwendet wird. Eigenschaften wie diese aufgrund von Macken der Testausrüstung werden technisch als Artefakte bezeichnet :Phänomene, die ausschließlich aufgrund einer Besonderheit der zur Durchführung des Experiments verwendeten Ausrüstung auftreten.

Wenn wir dieselbe Wechselspannung auf einem Spektrumanalysator betrachten, sieht das Ergebnis ganz anders aus:

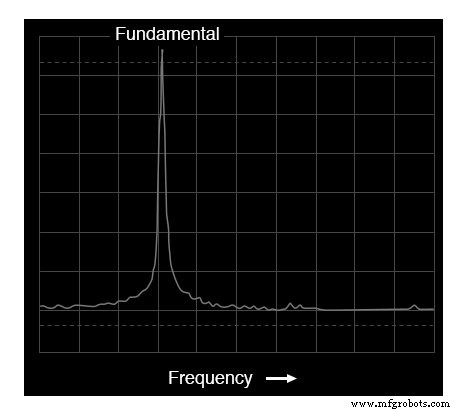
Spektrumanalysator-Anzeige:Spannung vs. Frequenz

Wie Sie sehen, ist die horizontale Achse der Anzeige mit dem Wort „Frequenz“ gekennzeichnet, das den Bereich dieser Messung bezeichnet. Der einzelne Peak auf der Kurve repräsentiert die Dominanz einer einzelnen Frequenz innerhalb des Frequenzbereichs, der von der Breite des Displays abgedeckt wird.

Wenn die Skala dieses Analysegeräts mit Zahlen markiert wäre, würden Sie sehen, dass dieser Peak bei 523,25 Hz auftritt. Die Höhe der Spitze stellt die Signalamplitude (Spannung) dar.

Mischen wir drei verschiedene Sinustöne auf dem elektronischen Keyboard (C-E-G, ein C-Dur-Akkord) und messen das Ergebnis, spiegeln sowohl die Oszilloskop- als auch die Spektrumanalysator-Anzeige diese erhöhte Komplexität wider:

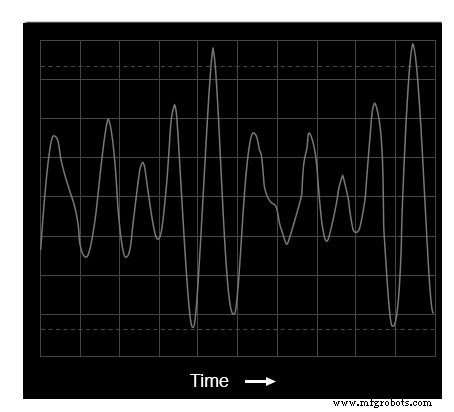
Oszilloscape-Anzeige:drei Töne

Die Oszilloskopanzeige (Zeitbereich) zeigt eine Wellenform mit viel mehr Spitzen und Tälern als zuvor, ein direktes Ergebnis der Mischung dieser drei Frequenzen. Wie Sie feststellen werden, sind einige dieser Spitzen höher als die Spitzen der ursprünglichen Single-Pitch-Wellenform, während andere niedriger sind.

Dies ist das Ergebnis der drei verschiedenen Wellenformen, die sich abwechselnd verstärken und aufheben, wenn sich ihre jeweiligen Phasenverschiebungen mit der Zeit ändern.

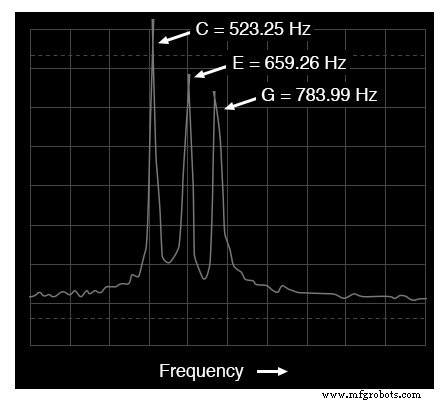
Spektrumanalysator-Anzeige:drei Töne

Die Spektrumdarstellung (Frequenzbereich) ist viel einfacher zu interpretieren:Jede Tonhöhe wird durch einen eigenen Peak auf der Kurve dargestellt. Der Höhenunterschied zwischen diesen drei Spitzen ist ein weiteres Artefakt der Testausrüstung:eine Folge von Einschränkungen innerhalb der Ausrüstung, die zum Erzeugen und Analysieren dieser Wellenformen verwendet wird, und keine notwendige Eigenschaft des musikalischen Akkords selbst.

Wie bereits erwähnt, ist das Gerät zur Erzeugung dieser Wellenformen eine elektronische Tastatur:ein Musikinstrument, das die Klänge vieler verschiedener Instrumente nachahmt.

Die Panflöte „Stimme“ wurde für die ersten Demonstrationen gewählt, weil sie einer reinen Sinuswelle (einer einzelnen Frequenz auf dem Display des Spektrumanalysators) am ähnlichsten war. Die „Stimmen“ anderer Musikinstrumente sind jedoch nicht so einfach wie diese. Tatsächlich ist der einzigartige Ton von any Instrument ist eine Funktion seiner Wellenform (oder seines Frequenzspektrums).

Sehen wir uns zum Beispiel das Signal für einen Trompetenton an:

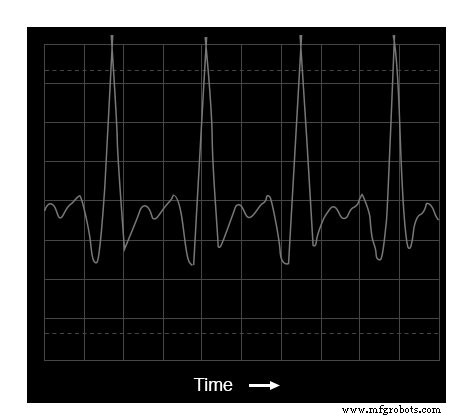
Oszilloskopdarstellung:Wellenform eines Trompetentons

Die Grundfrequenz dieses Tons ist dieselbe wie im ersten Panflötenbeispiel:523,25 Hz, eine Oktave über dem „mittleren C“.

Die Wellenform selbst ist weit entfernt von einer reinen und einfachen Sinuswellenform. Da wir wissen, dass jede sich wiederholende, nicht-sinusförmige Wellenform einer Reihe von Sinuswellenformen mit unterschiedlichen Amplituden und Frequenzen entspricht, sollten wir mehrere Spitzen auf der Anzeige des Spektrumanalysators erwarten:

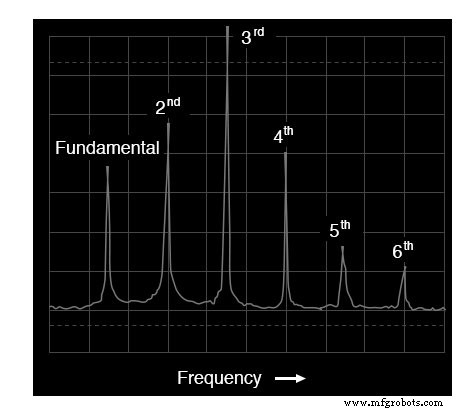
Spektrum eines Trompetentons

Tatsächlich tun wir das! Die Grundfrequenzkomponente von 523,25 Hz wird durch die Spitze ganz links dargestellt, wobei jede nachfolgende Harmonische als ihre eigene Spitze entlang der Breite des Analysatorbildschirms dargestellt wird.

Die zweite Harmonische hat die doppelte Frequenz der Grundwelle (1046,5 Hz), die dritte Harmonische dreimal die Grundfrequenz (1569,75 Hz) und so weiter. Dieses Display zeigt nur die ersten sechs Harmonischen, aber es gibt noch viele weitere, die diesen komplexen Ton umfassen.

Wenn wir eine andere Instrumentenstimme (das Akkordeon) auf der Tastatur ausprobieren, erhalten wir eine ähnlich komplexe Oszilloskop-(Zeitbereichs-)Darstellung und Spektrumanalysator-(Frequenzbereichs-)Anzeige:

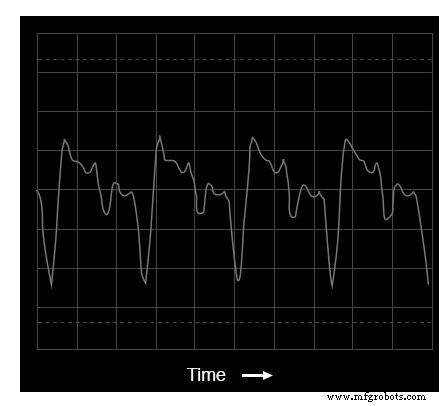
Oszilloskopanzeige:Wellenform des Akkordeontons

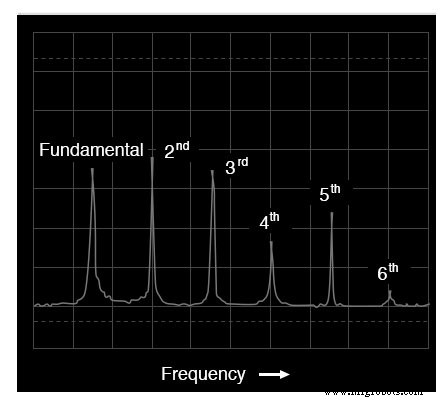
Spektrum des Akkordeonklangs

Beachten Sie die Unterschiede der relativen harmonischen Amplituden (Peakhöhen) in den Spektrumsanzeigen für Trompete und Akkordeon. Beide Instrumententöne enthalten Obertöne von der 1. (Grundton) bis zur 6. (und darüber hinaus!), aber die Proportionen sind nicht die gleichen.

Jedes Instrument hat eine einzigartige harmonische „Signatur“ für seinen Ton. Denken Sie daran, dass sich all diese Komplexität auf eine einzige Note bezieht mit diesen beiden Instrumenten „Stimmen“ gespielt. Mehrere auf einem Akkordeon gespielte Noten würden beispielsweise eine viel komplexere Mischung von Frequenzen erzeugen als hier gezeigt.

Die analytische Leistung des Oszilloskops und Spektrumanalysators erlaubt es uns, allgemeine Regeln über Wellenformen und ihre harmonischen Spektren aus realen Wellenformbeispielen abzuleiten. Wir wissen bereits, dass jede Abweichung von einer reinen Sinuswelle zu einer Mischung mehrerer Sinuswellenformen mit unterschiedlichen Amplituden und Frequenzen führt.

Eine genaue Beobachtung ermöglicht es uns jedoch, genauer zu sein. Beachten Sie beispielsweise die Zeit- und Frequenzbereichsdiagramme für eine Wellenform, die sich einer Rechteckwelle annähert:

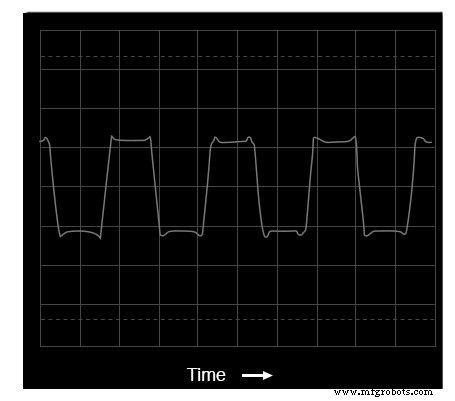
Oszilloskop-Zeitbereichsanzeige einer Rechteckwelle

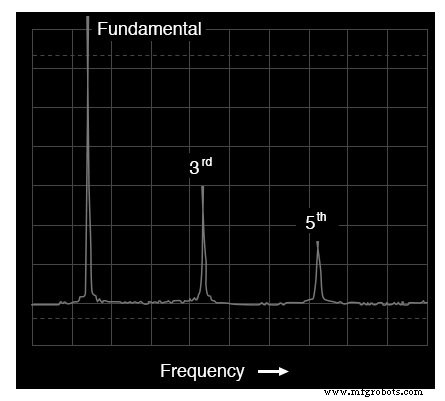
Spektrum (Frequenzbereich) einer Rechteckwelle

Laut Spektrumanalyse enthält diese Wellenform keine gerade Harmonische, nur ungerade. Obwohl diese Anzeige keine Frequenzen jenseits der sechsten Harmonischen anzeigt, setzt sich das Muster der nur ungeradzahligen Harmonischen in absteigender Amplitude unbegrenzt fort.

Dies sollte nicht überraschen, da wir bereits bei SPICE gesehen haben, dass eine Rechteckwelle aus unendlich vielen ungeraden Harmonischen besteht. Die Trompeten- und Akkordeontöne enthielten jedoch beide gerade und ungerade Harmonische.

Dieser Unterschied im harmonischen Gehalt ist bemerkenswert. Setzen wir unsere Untersuchung mit einer Analyse einer Dreieckswelle fort:

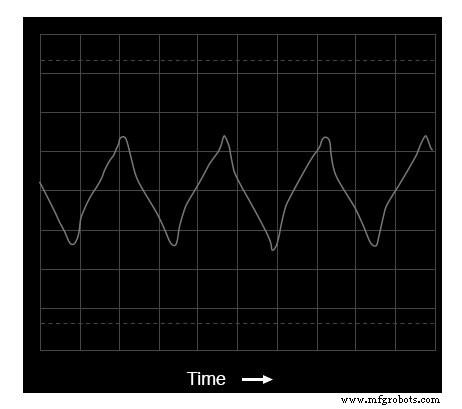
Oszilloskop-Zeitbereichsanzeige einer Dreieckswelle

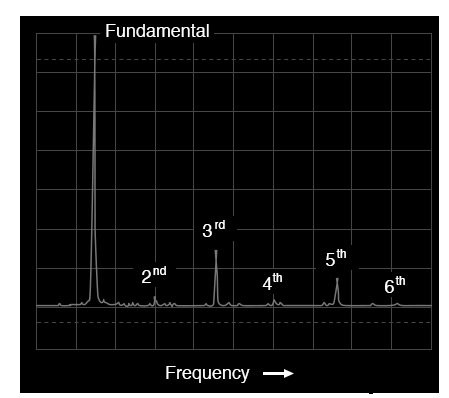
Spektrum einer Dreieckswelle

In dieser Wellenform gibt es praktisch keine geraden Oberwellen:(Abbildung oben) Die einzigen signifikanten Frequenzspitzen auf der Anzeige des Spektrumanalysators gehören zu ungeradzahligen Vielfachen der Grundfrequenz.

Für die zweite, vierte und sechste Harmonische sind winzige Spitzen zu sehen, dies ist jedoch auf Unvollkommenheiten in dieser speziellen Dreieckswellenform zurückzuführen (wiederum Artefakte der in dieser Analyse verwendeten Testausrüstung).

Eine perfekte Dreieckswellenform erzeugt keine gleichmäßigen Oberwellen, genau wie eine perfekte Rechteckwelle. Bei der Betrachtung sollte klar sein, dass das harmonische Spektrum der Dreieckswelle nicht identisch mit dem Spektrum der Rechteckwelle ist:Die jeweiligen harmonischen Spitzen sind unterschiedlich hoch. Die beiden unterschiedlichen Wellenformen sind jedoch insofern gemeinsam, als dass sie keine geraden Oberwellen haben.

Lassen Sie uns eine andere Wellenform untersuchen, die der Dreieckswelle sehr ähnlich ist, außer dass ihre Anstiegszeit nicht mit ihrer Abfallzeit übereinstimmt. Bekannt als Sägezahnwelle , zeigt sein Oszilloskop-Diagramm, dass es einen treffenden Namen hat:

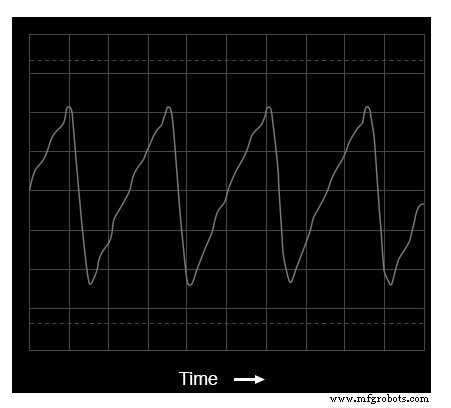
Zeitbereichsanzeige einer Sägezahnwelle

Wenn die Spektralanalyse dieser Wellenform aufgetragen wird, sehen wir ein Ergebnis, das sich stark von dem der regulären Dreieckswelle unterscheidet, denn diese Analyse zeigt das starke Vorhandensein von geradzahligen Harmonischen (zweite und vierte):

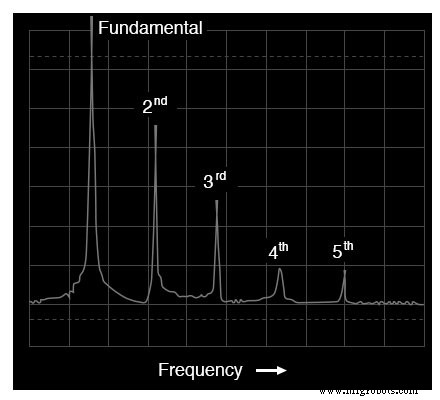
Frequenzbereichsdarstellung einer Sägezahnwelle

Der Unterschied zwischen einer Wellenform mit geraden Oberwellen und keinen geraden Oberwellen liegt im Unterschied zwischen einer Dreieckswellenform und einer Sägezahnwellenform.

Dieser Unterschied ist Symmetrie oberhalb und unterhalb der horizontalen Mittellinie der Welle. Eine Wellenform, die über und unter ihrer Mittellinie symmetrisch ist (die Formen auf beiden Seiten spiegeln einander genau) enthält nein geradzahlige Harmonische.

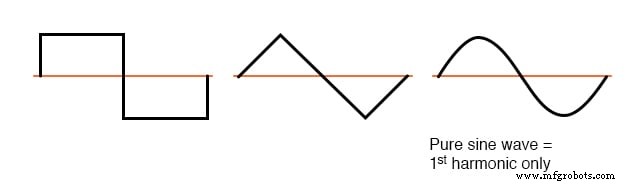
Wellenformen, die symmetrisch zu ihrer X-Achsen-Mittellinie sind, enthalten nur ungerade Harmonische

Rechteckwellen, Dreieckwellen und reine Sinuswellen weisen alle diese Symmetrie auf und alle sind frei von geraden Oberwellen. Wellenformen wie der Trompetenton, der Akkordeonton und die Sägezahnwelle sind um ihre Mittellinien unsymmetrisch und daher tun enthalten gerade Harmonische.

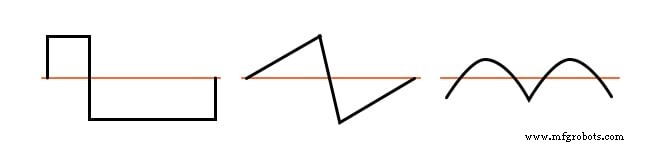
Asymmetrische Wellenformen enthalten gerade Obertöne

Dieses Prinzip der Mittelliniensymmetrie sollte nicht mit der Symmetrie um die Null verwechselt werden Linie. In den gezeigten Beispielen liegt die horizontale Mittellinie der Wellenform im Zeitbereichsdiagramm bei null Volt, dies hat jedoch nichts mit dem Oberwellengehalt zu tun.

Diese Regel des Oberwellengehalts (gerade Oberwellen nur bei unsymmetrischen Wellenformen) gilt unabhängig davon, ob die Wellenform mit einer „Gleichstromkomponente“ über oder unter null Volt verschoben wird. Zur weiteren Verdeutlichung zeige ich die gleichen Sätze von Wellenformen, verschoben mit der Gleichspannung, und beachte, dass ihr harmonischer Inhalt unverändert bleibt.

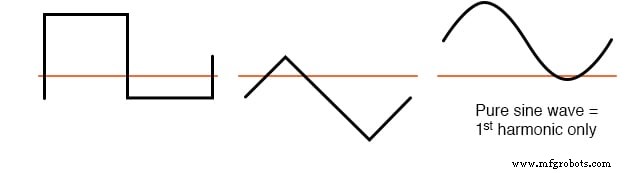
Diese Wellenformen bestehen ausschließlich aus ungeraden Harmonischen

Auch hier hat die Menge der in einer Wellenform vorhandenen Gleichspannung nichts mit dem harmonischen Frequenzgehalt dieser Wellenform zu tun.

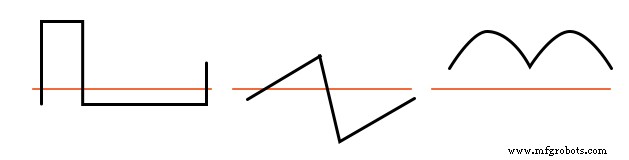
Diese Wellenformen enthalten gerade Obertöne

Warum ist es wichtig, diese harmonische Faustregel zu kennen? Es kann uns helfen, die Beziehung zwischen Oberwellen in Wechselstromkreisen und bestimmten Schaltungskomponenten zu verstehen.

Da die meisten Quellen von Sinuswellenverzerrungen in Wechselstromkreisen dazu neigen, symmetrisch zu sein, treten bei diesen Anwendungen selten geradzahlige Oberwellen auf.

Dies ist gut zu wissen, wenn Sie ein Netzplaner sind und die Reduzierung von Oberwellen vorausplanen:Sie müssen sich nur um die Abschwächung der ungeraden Oberwellenfrequenzen kümmern, da gerade Oberwellen praktisch nicht vorhanden sind.

Auch wenn Sie gerade Oberwellen in einem Wechselstromkreis mit einem Spektrumanalysator oder Frequenzmesser messen, wissen Sie, dass etwas in diesem Stromkreis unsymmetrisch sein muss die Sinusspannung oder den Sinusstrom verzerren, und dieser Hinweis kann hilfreich sein, um die Ursache eines Problems zu lokalisieren (suchen Sie nach Komponenten oder Bedingungen, die eine Halbwelle der AC-Wellenform eher verzerren als die andere).

Da wir nun diese Regel haben, um unsere Interpretation nichtsinusförmiger Wellenformen zu leiten, ist es sinnvoller, dass eine Wellenform, wie sie von einer Gleichrichterschaltung erzeugt wird, so starke gerade Oberwellen enthalten sollte, dass es über und unter der Mitte keinerlei Symmetrie gibt.

RÜCKBLICK:

• Symmetrische Wellenformen oberhalb und unterhalb ihrer horizontalen Mittellinie enthalten keine geradzahligen Harmonischen.
• Der Betrag der vorhandenen DC-"Bias"-Spannung (die "DC-Komponente einer Wellenform") hat keinen Einfluss auf den harmonischen Frequenzgehalt dieser Welle.

VERWANDTE ARBEITSBLÄTTER:

• Arbeitsblatt für die grundlegende Oszilloskop-Bedienung
• Arbeitsblatt für passive Integrator- und Differentiatorschaltungen