Überlagerungssatz – Schaltungsanalyse mit gelöstem Beispiel

Superpositionssatz – Schritt-für-Schritt-Anleitung mit gelöstem Beispiel

Was ist der Superpositionssatz?

Das Superpositionstheorem wird verwendet, um komplexe Netzwerke mit mehreren Energiequellen zu lösen. Es ist ein wichtiges Konzept, Spannung und Strom über die Elemente zu bestimmen, indem die Wirkung jeder Quelle einzeln berechnet wird. Und kombinieren Sie die Wirkung aller Quellen, um die tatsächliche Spannung und den tatsächlichen Strom des Schaltungselements zu erhalten.

Überlagerungssatz besagt, dass;

Mit anderen Worten, wir betrachten jeweils nur eine unabhängige Quelle. Also müssen wir andere Quellen entfernen. Bei idealen Quellen sind die Spannungsquellen kurzgeschlossen und die Stromquellen offen. Wenn der Innenwiderstand von Quellen angegeben ist, müssen Sie die Schaltung berücksichtigen.

Der Superpositionssatz wird nur auf die Schaltung angewendet, die dem Ohmschen Gesetz folgt.

• Verwandter Beitrag:Thevenin’s Theorem. Schritt-für-Schritt-Anleitung mit gelöstem Beispiel

Wann sollte das Superpositionstheorem verwendet werden?

Das Netzwerk muss die folgenden Anforderungen erfüllen, um das Superpositionstheorem anzuwenden.

• Die in der Schaltung verwendeten Komponenten müssen linear sein. Bei Widerständen bedeutet dies, dass der Stromfluss proportional zur Spannung ist; Bei Induktivitäten ist die Flussverkettung proportional zum Strom. Daher sind der Widerstand, die Induktivität und der Kondensator lineare Elemente. Aber die Diode, der Transistor ist kein lineares Element.
• Die Schaltungskomponenten müssen zweiseitige Elemente sein. Das bedeutet, dass die Stärke des Stroms unabhängig von der Polarität der Energiequellen ist.
• Mit Hilfe des Superpositionssatzes können wir den Stromfluss durch ein Element, den Spannungsabfall des Widerstands und die Knotenspannung ermitteln. Aber wir können die vom Element abgegebene Energie nicht finden.

• Verwandter Beitrag:Theorem von Norton. Schritt-für-Schritt-Anleitung mit gelöstem Beispiel

Schritte zum Befolgen des Superpositionssatzes

Schritt-1 Informieren Sie sich über eine Reihe unabhängiger Quellen, die im Netzwerk verfügbar sind.

Schritt-2 Wählen Sie eine beliebige Quelle und eliminieren Sie alle anderen Quellen. Wenn das Netzwerk aus einer abhängigen Quelle besteht, können Sie es nicht eliminieren. Sie bleibt während der gesamten Berechnung unverändert.

Wenn Sie alle Energiequellen als ideale Quellen angesehen haben, brauchen Sie den Innenwiderstand nicht zu berücksichtigen. Und direkt Kurzschlussspannungsquelle und Leerlaufstromquelle. Aber falls der Innenwiderstand der Quellen gegeben ist, müssen Sie den Innenwiderstand ersetzen.

Schritt-3 Nun ist in einem Stromkreis nur noch eine unabhängige Energiequelle vorhanden. Sie müssen eine Antwort mit nur einer Energiequelle im Stromkreis finden.

Schritt-4 Wiederholen Sie die Schritte 2 und 3 für alle im Netzwerk verfügbaren Energiequellen. Wenn es drei unabhängige Quellen gibt, müssen Sie diese Schritte dreimal wiederholen. Und jedes Mal erhalten Sie einen gewissen Wert der Antwort.

Schritt-5 Kombinieren Sie nun alle Antworten durch algebraische Summierung, die von einzelnen Quellen erhalten wurden. Und Sie erhalten einen endgültigen Antwortwert für ein bestimmtes Element eines Netzwerks. Wenn Sie eine Antwort für andere Elemente finden müssen, müssen Sie diese Schritte für dieses Element erneut ausführen.

• Verwandter Beitrag: SUPERMESH-Schaltkreisanalyse – Schritt für Schritt mit gelöstem Beispiel

Beispiel für ein gelöstes Superpositionstheorem

Beispiel:

Lassen Sie uns die Funktionsweise des Superpositionssatzes anhand eines Beispiels verstehen. Finde den Strom (I_L ) durchläuft den 8Ω-Widerstand im gegebenen Netzwerk unter Verwendung des Superpositionssatzes.

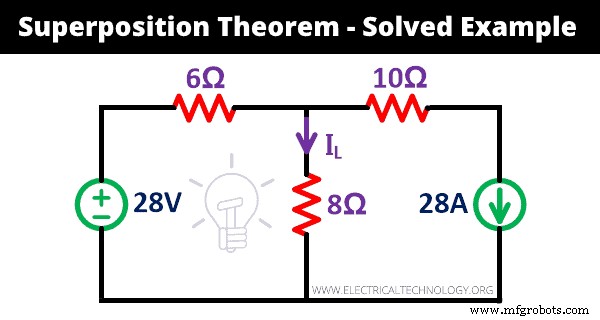
Lösung:

Schritt-1 Wie im obigen Netzwerk gezeigt, ist eine Spannungsquelle und eine Stromquelle gegeben. Daher müssen wir den Vorgang zweimal wiederholen.

Schritt-2 Zuerst betrachten wir eine 28-V-Spannungsquelle im Netzwerk. Sie müssen also die Stromquelle durch offene Klemmen entfernen. Wie hier betrachten wir die Stromquelle als ideale Stromquelle. Also müssen wir den Innenwiderstand nicht anschließen.

Die verbleibende Schaltung ist wie in der folgenden Abbildung dargestellt.

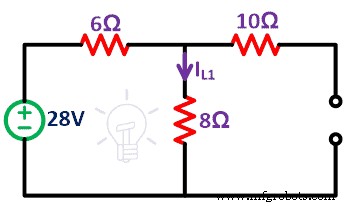
Schritt-3 Finde den Strom (I_L1 ) geht durch 8Ω Widerstand. Es wirkt nur wie eine Spannungsquelle.

Aufgrund des offenen Stromkreises einer Stromquelle fließt kein Strom durch den 10Ω-Widerstand. Das Netzwerk besteht also nur aus einer Schleife.

Wende KVL auf die Schleife an;

28 =6Ich _{L 1} + 8Ich _{L 1}

28 =14I _{L 1}

Ich _{L 1} =28/14

Ich _{L 1} =2A

Schritt-4 Jetzt wiederholen wir das gleiche Verfahren für die aktuelle Quelle. In diesem Zustand entfernen wir die Spannungsquelle durch Kurzschließen. Eine verbleibende Schaltung ist in der folgenden Abbildung dargestellt.

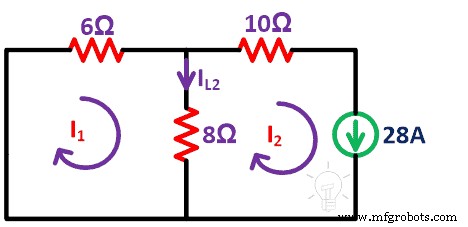
Hier müssen wir zwei Schleifen betrachten. Ich₁ und I₂ Schleifenstrom sind. Und finden Sie den aktuellen I_L2 .

KVL auf Loop-1 anwenden;

0 =6Ich ₁ + 8Ich ₁ – 8Ich ₂

14Ich ₁ – 8Ich ₂ =0

Der Strom fließt durch die Schleife-2 wird aus der Stromquelle berechnet. Und es wird sein;

Ich ₂ =28A

Setzen Sie diesen Wert in die obige Gleichung ein;

14Ich ₁ – 8 (28) =0

Ich ₁ =16A

Jetzt ist der 8Ω-Widerstandszweig in beiden Schleifen gemeinsam. Also müssen wir den resultierenden Strom finden (I_L2 ) geht durch den 8Ω-Widerstand.

Ich _{L 2} =ich ₁ – ich ₂

Ich _{L 2} =16 – 28

Ich _{L 2} =-12A

Schritt-5 Jetzt kombinieren wir die Wirkung beider Quellen durch algebraische Summierung des Stroms. Der Gesamtstrom, der durch den 8Ω-Widerstand fließt, ist also I_L . Hier ist die Richtung des Stroms am wichtigsten. Strom I_L2 hat ein Minuszeichen. Dies bedeutet, dass während der 28A-Quelle der Strom in entgegengesetzter Richtung fließt. Und wir können die Richtung nicht ändern. Das ist der Grund, warum wir beim Kombinieren aller Quellen eine algebraische Summierung durchführen.

Ich _L =I_{L 1} – I_{L 2}

Ich _L =2 + (-12)

Ich _L =-10A

Hier haben wir angenommen, dass der Strom durch den 8Ω-Widerstand in Richtung des in der Abbildung gezeigten Pfeils fließt. Das Minuszeichen zeigt die entgegengesetzte Richtung an. Und die Stromstärke beträgt 8A.

• Verwandter Beitrag:SUPERNODE-Schaltungsanalyse – Schritt für Schritt mit gelöstem Beispiel

Superpositionstheorem-Experiment

Das Superpositionstheorem-Experiment kann mit den folgenden Schritten durchgeführt werden.

Ziel

Bestimmen Sie den Strom, der durch die Widerstände fließt, und verifizieren Sie den Superpositionssatz.

Erforderliche Komponenten

DC-Quelle, Widerstände, DC-Multimeter, Verbindungskabel, Steckbrett usw.

Theorie

Der Superpositionssatz wird in der Schaltungsanalyse verwendet, um den Strom und die Spannung über den Elementen in einer bestimmten Schaltung zu ermitteln. Dieser Satz ist nützlich, wenn die Anzahl der Quellen größer ist.

Gemäß dem Überlagerungssatz ist die Antwort der Elemente eine algebraische Summierung der Antwort der einzelnen Energiequellen.

Zuerst berechnen wir den Stromfluss durch die Widerstände in einem gegebenen Netzwerk. Wenn alle Quellen angeschlossen sind. Danach entfernen wir Quellen und finden Strömungen für einzelne Quellen. Schließlich ist die Summierung des von den einzelnen Quellen gemessenen Stroms ähnlich den Strommessungen mit allen angeschlossenen Quellen.

Vorgehensweise

Wir betrachten die in der folgenden Abbildung angegebene lineare bilaterale Schaltung.

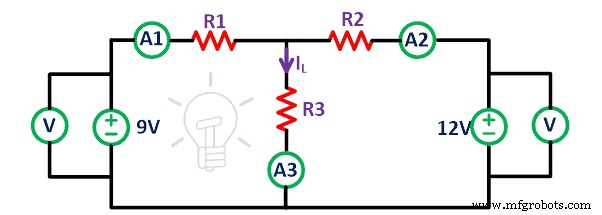
Verbinde alle Elemente auf dem Steckbrett wie in der obigen Schaltung angegeben mit Verbindungsdrähten. Schließen Sie ein Amperemeter an alle Widerstände an, um den Strom zu ermitteln, der durch die Widerstände fließt. Hier haben wir zwei Spannungsquellen.

Messen Sie im ersten Fall den Strom, der durch alle Widerstände fließt, wenn beide Spannungsquellen im Stromkreis vorhanden sind. Der Strom, der durch den Widerstand R₁ fließt , R₂ , und R₃ ist ich ₁ , ich ₂ , und ich ₃ bzw..

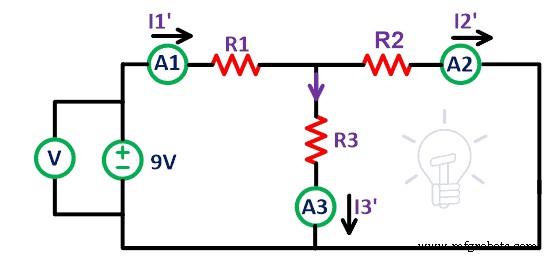
Entfernen Sie nun die 12V-Spannungsquelle vom Stromkreis. Schließen Sie die Klemmen A’ und B’ wie in der obigen Abbildung gezeigt kurz. Hier haben wir angenommen, dass die Spannungsquellen ideal sind. Es muss also kein Innenwiderstand angeschlossen werden. Messen Sie nun den Strom I _1′ , ich _2′ und ich _3′ das ist der Strom, der durch die Widerstände R1, R2 bzw. R3 fließt.

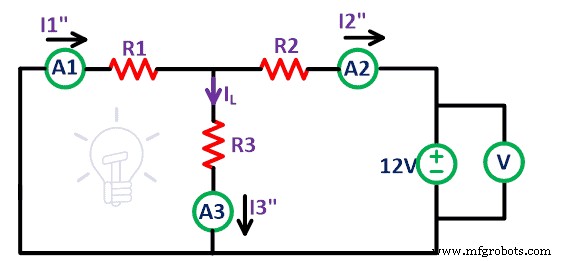
Entfernen Sie auf ähnliche Weise die 9-V-Spannungsquelle und der verbleibende Stromkreis ist wie in der obigen Abbildung gezeigt. Messen Sie wieder den Strom, der durch alle Widerstände fließt, und nennen Sie ihn I _{1 “} , ich _{2 “} , und ich _{3 “} .

• Verwandter Beitrag: Theorem der maximalen Leistungsübertragung für AC- und DC-Schaltungen

Tragen Sie alle Werte in die folgende Beobachtungstabelle ein.

Beobachtungstabelle

Quellverbindung	R1	R2	R3
Beide Quellen sind verbunden	Ich 1	Ich 2	Ich 3
Nur 12V sind angeschlossen	Ich 1′	Ich 2′	Ich 3′
Nur 9V sind angeschlossen	Ich 1″	Ich 2″	Ich 3″

Berechnung :

Ich ₁ =ich _1′ + ich _1″

Ich ₂ =ich _2′ + ich _2″

Ich ₃ =ich _3′ + ich _3″

Um das Superpositionstheorem zu verifizieren, vergleichen wir die algebraische Summierung von Stromflüssen durch Widerstände, wenn eine einzelne Quelle verbunden ist, mit dem Strom, der gemessen wird, wenn beide Quellen in einem Stromkreis verbunden sind.

P>

Wenn die obige Rechnung erfüllt ist, können wir den Superpositionssatz beweisen.

Fazit

In diesem Experiment können wir beweisen, dass der Strom, der durch den Widerstand fließt, eine algebraische Summe des Stroms ist, wenn eine einzelne Energiequelle angeschlossen ist. Und es beweist den Superpositionssatz.

• Verwandter Beitrag:Kirchhoffs Strom- und Spannungsgesetz (KCL &KVL) | Gelöstes Beispiel

Anwendung des Superpositionssatzes

• Der Superpositionssatz kann für AC- und DC-Netze verwendet werden.
• Wenn die Anzahl unabhängiger Quellen größer ist, ist es einfach, eine Antwort des Netzwerks zu finden.
• Es hilft, Stromdurchgänge und die Spannung über dem Element zu berechnen, indem die Wirkung jeder Energiequelle einzeln berechnet wird. Und nachdem wir die kombinierte Wirkung auf Elemente aus allen Quellen bestimmen können.

Nachteil des Superpositionssatzes

• Der Superpositionssatz kann nicht auf Schaltungen angewendet werden, die nur eine abhängige Quelle haben. Es brauchte mindestens zwei unabhängige Quellen.
• Dieses Theorem gilt nur für das Netzwerk, das aus linearen Elementen besteht. Es kann nicht auf nichtlineare Elemente wie Dioden, Transistoren usw. angewendet werden
• Wir können die Leistung nicht mit diesem Theorem berechnen. Da die Leistung proportional zum Quadrat von Spannung und Strom ist, wird sie nichtlinear.
• Dieses Theorem ist nicht anwendbar, wenn der Widerstand mit Spannung und Strom variiert. Bei allen Energiequellen muss der Widerstandswert konstant bleiben.
• Dieses Theorem gilt nur für die bilateralen Elemente. Wenn die Antwort des Netzwerks von der Richtung des Stroms abhängt, ist dieser Satz nicht anwendbar.

Verwandte Tutorials zur Analyse elektrischer Schaltungen:

• Theorem von Tellegen – Gelöste Beispiele &MATLAB-Simulation
• Cramers Rule Calculator – 2- und 3-Gleichungssystem für elektrische Schaltungen
• Wheatstone Bridge – Schaltung, Funktionsweise, Ableitung und Anwendungen
• Rechner für Elektrotechnik und Elektronik
• 5000+ elektrische und elektronische Formeln und Gleichungen