Satz von Tellegen – Gelöste Beispiele und MATLAB-Simulation

Satz von Tellegen – Schritt-für-Schritt-Anleitung mit gelösten Beispielen

Was ist der Satz von Tellegen?

Satz von Tellegen wurde von einem niederländischen Elektroingenieur und Erfinder Bernard D.H. Tellegen veröffentlicht im Jahr 1952. Dieser Satz ist der wichtigste und grundlegendste Satz unter anderen Sätzen in der Netzwerkanalyse. Die meisten anderen Theoreme werden von diesem Theorem abgeleitet.

Der Satz von Tellegen hängt vom Kirchhoffschen Gesetz ab. Daher kann dieser Satz auf das Netzwerk angewendet werden, das dem Kirchhoffschen Gesetz gehorcht. Dieses Theorem kann auf den weiten Bereich des Netzwerks mit linearen oder nichtlinearen, zeitvarianten oder nichtvarianten, passiven oder aktiven Elementen angewendet werden.

Der Satz von Tellegen besagt Folgendes:

Der Satz von Tellegen funktioniert auf der Grundlage des Energieerhaltungssatzes. Dieses Theorem wird in chemischen und biologischen Anwendungen verwendet, um das dynamische Verhalten des physikalischen Netzwerks zu ermitteln. In der Signalverarbeitung wird dieses Theorem zum Entwerfen von Filtern verwendet.

• Verwandter Beitrag:Thevenin’s Theorem. Schritt-für-Schritt-Anleitung mit gelöstem Beispiel

Mathematische Gleichung

Für eine allgemeine Analyse des Theorems betrachten wir die im Netzwerk gegebene Anzahl von n Elementen. Der Momentanstrom, der durch das Element fließt, ist i₁ , i₂ , i₃ , …., i_n . Und die Momentanspannung dieses Zweigs ist v₁ , v₂ , v₃ , …., v_n .

Daher sind der momentane Strom und die Spannung von Element-1 i₁ und v₁ . Die Momentanleistung (p₁ ) von diesem Element verbraucht wird, ist v₁ i₁ .

p ₁ =v ₁ ich ₁

Die Momentanleistung von Element-2 ist (p ₂ );

p ₂ =v ₂ ich ₂

Ähnlich die momentane Leistung von n ^th Element ist (p _n );

p_n =v_n i_n

Nach dem Satz von Tellegen ist die Summe aller Momentanleistungen null. Das bedeutet, dass wir alle Momentanleistungen p₁ summieren müssen , p₂ , p₃ , …., p_n .

p ₁ + p ₂ + p ₃ + … + p_n = 0

v ₁ ich ₁ +v ₂ ich ₂ + v ₃ ich ₃ + … + v_n i_n  = 0

In allgemeiner Form können wir die obige Gleichung für den k ^ten schreiben Zweig;

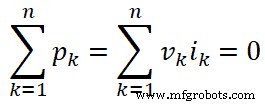
Wo,

• n =Gesamtzahl der Filialen im Netzwerk
• v_k =momentane Spannung von k ^th Filiale
• i_k =momentaner Strom von k ^th Filiale
• p_k =Momentanleistung von k ^th Filiale

Betrachten Sie nun die folgende Abbildung als Zweig AB ist gleich Zweig k.

Also Momentanspannung v_k ;

v_k =v_ein – v_b

Und der momentane Strom, der durch den Zweig (a nach b) fließt, ist i_k ;

i_k =i_ab

Also die Momentanleistung p_k ist;

p_k =v_k i_k =(v_a –v_b ) i_ab ….. (1)

Jetzt betrachten wir die entgegengesetzte Richtung des Momentanstroms (b nach a);

i_ab =– i_ab

Momentanspannung;

v_k =v_b – v_a

Die Momentanleistung p_k ist;

p_k =v_k i_k =(v_b –v_a ) i_ba ….. (2)

Summierung von Gleichung 1 und 2;

2v_k i_k =(v_a –v _b )ich _ab + (v_b – v_a ) i_ba

v_k i_k =1/2 [(v_a –v _b )ich _ab + (v_b – v_a )i_ba ] ….. (3)

Diese Gleichung kann wie folgt für n-Zweige geschrieben werden;

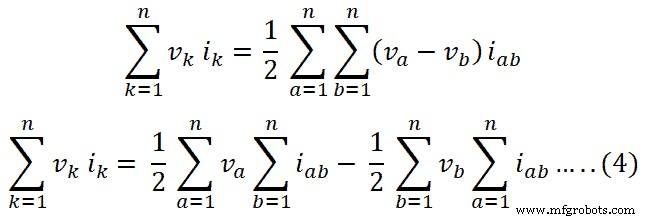
Nach dem aktuellen Gesetz von Kirchhoff ist die algebraische Summe des Stroms an einem Knoten der Schaltung null.

Daher

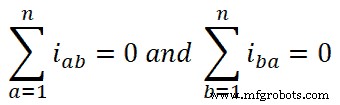
Wenn wir diesen Wert in die Gleichung-4 einsetzen, erhalten wir;

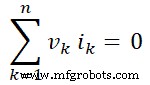
Damit ist bewiesen, dass die Summe der an das Netz gelieferten Leistung Null ist. Damit ist der Satz von Tellegen bewiesen. Es wird auch beschrieben, dass die Summe der von den Elementen des Netzes aufgenommenen Leistung gleich der Summe der von den Quellen gelieferten Leistung ist.

• Verwandter Beitrag:Theorem von Norton. Schritt-für-Schritt-Anleitung mit gelöstem Beispiel

Zu befolgende Schritte für den Satz von Tellegen

Wir müssen die folgenden Schritte befolgen, um jedes elektrische Netzwerk nach dem Satz von Tellegen zu lösen.

Schritt-1: Wir müssen eine Reihe von Abzweigungen in dem gegebenen Stromnetz finden. Finden Sie dann die Verlustleistung über jeden Zweig. Um die Leistung zu finden, müssen wir die Spannung oder den Strom dieses Zweigs mit einer herkömmlichen Analysemethode ermitteln.

Schritt-2: Ermitteln Sie die Momentanleistung jedes Zweigs.

Schritt-3: Der Zweig, der eine Energiequelle hat, die als stromliefernder Zweig betrachtet wird. Und der Zweig hat andere Elemente und wird als stromabsorbierender Zweig betrachtet. Identifizieren Sie nun den Strom abgebenden Zweig und den Strom aufnehmenden Zweig.

Schritt-4: Nehmen Sie ein positives Vorzeichen im leistungsliefernden Zweig und einen negativen Spannungsabfall im leistungsabsorbierenden Zweig an. Sie können auch umgekehrte Vorzeichen annehmen. Kann sich aber im gesamten Beispiel nicht ändern.

Schritt-5: Um den Satz von Tellegen zu rechtfertigen, müssen wir alle aus allen Zweigen berechneten Leistungen addieren. Und diese Summe ist immer Null.

• Verwandter Beitrag: SUPERMESH-Schaltkreisanalyse – Schritt für Schritt mit gelöstem Beispiel

Lass es uns anhand eines Beispiels verstehen.

Beispiel für das gelöste Theorem von Tellegen

Beispiel #1

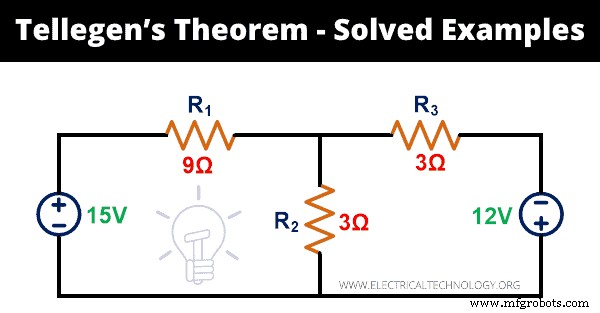
Begründen Sie den Satz von Tellegen für das folgende Netzwerk.

Lösung:

Schritt-1: Das gegebene Schaltungsnetz hat 5 Zweige. Um die Momentanleistung zu berechnen, müssen wir die Stromdurchgänge durch jeden Zweig finden. Dafür werden wir KVL auf das Netzwerk anwenden.

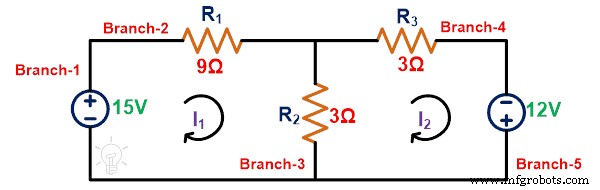
KVL auf Loop-1 anwenden;

15 =12Ich ₁ – 3ich ₂

KVL auf Loop-2 anwenden;

12 =– 3Ich ₂ + 6Ich ₂

Durch Lösen der obigen Gleichungen können wir die Werte des Schleifenstroms I₁ finden und I₂ . Und diese Werte sind:

Ich ₁ =2A

Ich ₂ =3A

Schritt-2: Strom, der durch den Zweig-3 fließt, ist;

Ich _{1 2} =ich ₂ – ich ₁ =3 – 2 =1A

Wir haben Stromfluss durch alle Zweige. Finden Sie jetzt die Stärke jedes Zweigs heraus.

P ₁ =V I ₁ =15 x 2 =30 W

P ₂ =R ₁ Ich ₁ ² =9 x 4 =36 W

P ₃ =R ₁ Ich ₁₂ ² =3 x 1 =3W

P ₄ =R ₃ Ich ₂ ² =3 x 9 =27 W

P ₅ =V I ₂ =12 x 3 =36 W

Schritt-3: Es gibt zwei Zweige mit Quellen. Diese Zweige sind stromliefernde Zweige und die anderen drei Zweige sind stromabsorbierende Zweige.

Hier nehmen wir für dieses Beispiel an, dass das Vorzeichen des leistungsabgebenden Zweigs positiv und das Vorzeichen des leistungsaufnehmenden Zweigs negativ ist. Daher sind Zweig 1 und 5 stromliefernde Zweige und andere Zweige sind stromabsorbierende Zweige.

Schritt-4: Das Zeichen der Leistung P₁ und P₅ positiv ist (Strom liefernde Zweige) und das Vorzeichen von P₂ , P₃ , und P₄ ist negativ (Strom absorbierende Zweige).

Schritt-5: Jetzt müssen wir eine Summe der von allen Zweigen verbrauchten Leistung finden.

P ₁ – P ₂ – P ₃ – P ₄ + P ₅ =30 W – 36 W – 3 W – 27 W + 36 W =0 W

Die Summe der Momentanleistung ist also Null. Und damit ist dieser Satz bewiesen.

• Verwandter Beitrag:SUPERNODE-Schaltungsanalyse – Schritt für Schritt mit gelöstem Beispiel

Beispiel Nr. 2

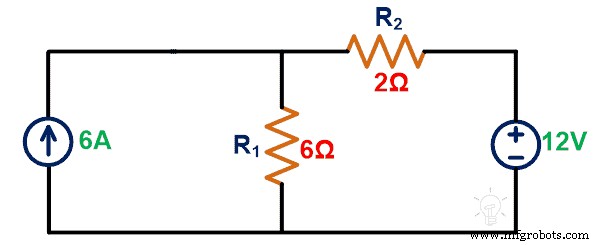
Finden Sie die Spannung über einer 6-A-Stromquelle mithilfe des Satzes von Tellegen.

Lösung:

Schritt-1: Wir müssen die Spannung oder den Strom berechnen, der durch das Element fließt. Dafür wenden wir KCL oder KVL auf das angegebene Netzwerk an.

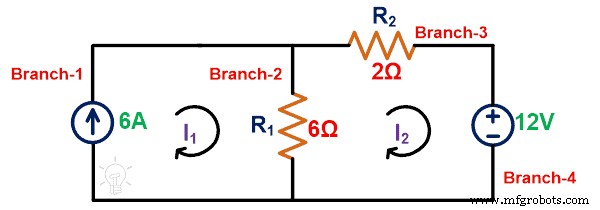
KVL auf Loop-2 anwenden;

-12 =8I ₂ – 6ich ₁

Aktueller Durchgang durch den Zweig mit aktueller Quelle ist I ₁;

Ich ₁ =6A

Setzen Sie diesen Wert in die obige Gleichung ein;

-12 =8I ₂ – 6(6)

-12 =8I ₂ – 36

36 – 12 =8I ₂

24 =8Ich ₂

Ich ₂ =3A

Schritt-2: Strom fließt durch den Zweig-2 ist;

Ich ₁₂ =ich ₁ – ich ₂ =6 – 3 =3A

Finden Sie jetzt die Kraft jedes Zweigs heraus;

P ₁ =V I ₁ =V x 6 =6 x V

P ₂ =R ₁ Ich ₁₂ ² =6 x 9 =54 W

P ₄ =R ₂ Ich ₂ ² =2 x 9 =18 W

P ₄ =V I ₂ =-12 x 3 =-36 W

Schritt-3: Hier zwei Äste mit Energiequellen. Daher müssen wir diese Zweige als stromliefernde Zweige betrachten. Und setze das positive Vorzeichen auf die Momentanleistung.

Die anderen beiden Zweige haben nur Widerstände. Diese Zweige sind also leistungsabsorbierende Zweige und setzen der Momentanleistung das negative Vorzeichen.

Schritt-4: Leistung P₁ und P₄ haben ein positives Vorzeichen und eine Potenz P₂ und P3 haben ein negatives Vorzeichen.

Schritt-5: Jetzt müssen wir die gesamte Momentanleistung zusammenfassen.

P ₁ – P ₂ – P ₃ + P ₄ =0W

P ₁ – 54 – 18 + 36 =108 W

Die von der 6-A-Stromquelle gelieferte Leistung beträgt 108 W. Daher wird die Spannung über der Stromquelle berechnet durch;

P ₁ =V I

108W =V x 6A

V =18V

Daher beträgt die Spannung über der Stromquelle 18 V.

• Verwandter Beitrag: Theorem der maximalen Leistungsübertragung für AC- und DC-Schaltungen

Analyse und Simulation des Satzes von Tellegen mit MATLAB  

Ziel:

Beweise den Satz von Tellegen für den im obigen Beispiel angegebenen Schaltplan.

Anforderung: MATLAB

Theorie:

Gemäß dem Satz von Tellegen ist die summierte Momentanleistung aller Zweige gleich Null. Um dieses Theorem zu beweisen, müssen wir die Momentanleistung aller Zweige berechnen.

Um die momentane Leistung zu finden, müssen wir die Spannung oder den Strom aller Zweige berechnen. Dafür können wir KCL- oder KVL-Theoreme verwenden. Aber hier werden wir das MATLAB Simulink-Modell verwenden, um den Strom und die Spannung zu finden.

Wir können auch andere Software wie Multisim, Psim usw. verwenden. Wir werden einen Schaltplan im Simulink-Modell erstellen. Durch das Simulink-Modell können Sie die Spannung und den Strom von jedem Zweig finden.

Danach können Sie die Momentanleistung aus Spannung und Strom ermitteln. Sie können die Momentanleistung direkt von einer Software finden.

MATLAB-Simulink-Modell

Die folgende Abbildung zeigt den Schaltplan des obigen Beispiels.

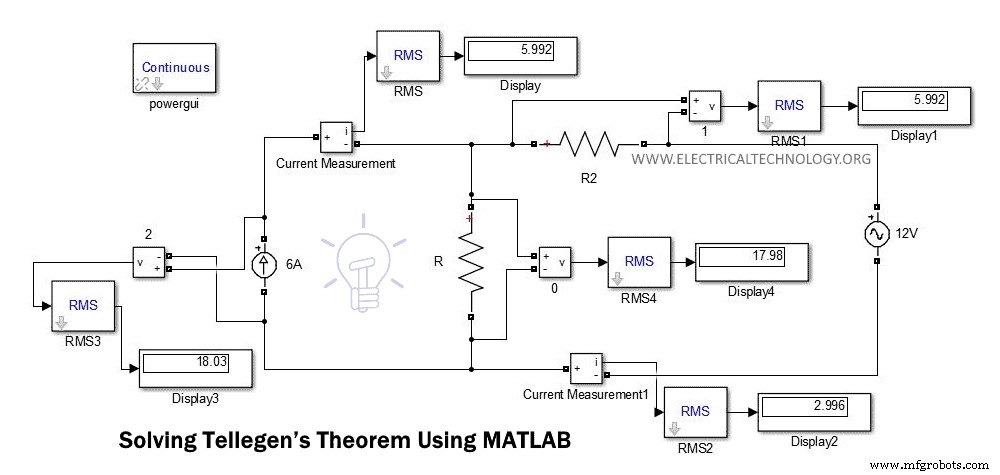
In dieser Abbildung können wir die Spannung und den Strom direkt auf dem Display finden. Sie können diese Werte vergleichen, indem Sie die Spannung und den Strom mit Hilfe von KCL oder KVL berechnen.

Berechnung

Nachdem Sie Spannung oder Strom berechnet haben, können Sie die Momentanleistung finden. Oder Sie können die Momentanleistung direkt aus der Software ermitteln. Alles, was wir brauchen, ist sofortige Energie. Und danach müssen wir alle Kräfte hinzufügen.

Die Summierung der Leistung ist immer Null. Für dieses Beispiel vergleichen wir den in Simulink gefundenen Spannungs- und Stromwert mit denselben Werten, die im vorherigen Beispiel unter Verwendung von KVL und KCL berechnet wurden. Diese Werte sind identisch.

Diese Werte werden auch von den Anschlusswiderständen und Quellen auf dem Steckbrett berechnet. Und wir können die Spannung und den Strom, der durch alle Zweige fließt, mit Hilfe eines Voltmeters und eines Amperemeters messen.

Daher ist der Satz von Tellegen bewiesen.

• Verwandter Beitrag:Kirchhoffs Strom- und Spannungsgesetz (KCL &KVL) | Gelöstes Beispiel

Anwendung des Satzes von Tellegen

Dieses Theorem ist sehr grundlegend und wird häufig in der Schaltungsanalyse verwendet. Es gibt viele Anwendungen dieses Theorems. Einige Anwendungen sind unten aufgeführt.

• Für den Entwurf der Filter ist dieses Theorem sehr nützlich in den Anwendungen der digitalen Signalverarbeitung.
• Um die Stabilität chemischer Anlagen zu bestimmen, wird dieser Satz in der chemischen Verfahrenstechnik verwendet.
• Dieses Theorem gilt für das konzentrierte System mit linear-nichtlinearen, aktiv-passiven, zeitvarianten/zeitinvarianten Elementen.
• Dieses Theorem wird im biologischen Prozess verwendet.
• Es wird in der Topologie und Analyse von Strukturreaktionen verwendet.
• Es wird auch verwendet, um das dynamische Verhalten des physischen Netzwerks zu finden.

Verwandte Tutorials zur Analyse elektrischer Schaltungen:

• Superpositionssatz – Schaltungsanalyse mit gelöstem Beispiel
• Cramers Rule Calculator – 2- und 3-Gleichungssystem für elektrische Schaltungen
• Wheatstone-Brücke – Schaltung, Funktionsweise, Ableitung und Anwendungen
• Rechner für Elektrotechnik und Elektronik
• 5000+ elektrische und elektronische Formeln und Gleichungen