So trainieren Sie ein mehrschichtiges neuronales Perceptron-Netzwerk

Wir können die Leistung eines Perceptrons erheblich verbessern, indem wir eine Schicht versteckter Knoten hinzufügen, aber diese versteckten Knoten machen das Training auch etwas komplizierter.

Bisher haben Sie in der AAC-Serie über neuronale Netze etwas über die Datenklassifizierung mit neuronalen Netzen gelernt, insbesondere vom Typ Perceptron.

Informieren Sie sich über die untenstehende Serie oder tauchen Sie in diesen neuen Eintrag ein, der die Grundlagen des neuronalen Mehrschichtnetzwerks Perceptron (MLP) erklärt.

1. Wie man eine Klassifikation mit einem neuronalen Netzwerk durchführt:Was ist das Perzeptron?
2. So verwenden Sie ein einfaches Beispiel für ein neuronales Perceptron-Netzwerk zum Klassifizieren von Daten
3. Wie man ein grundlegendes neuronales Perceptron-Netzwerk trainiert
4. Einfaches neuronales Netzwerk-Training verstehen
5. Eine Einführung in die Trainingstheorie für neuronale Netze
6. Lernrate in neuronalen Netzen verstehen
7. Fortgeschrittenes maschinelles Lernen mit dem mehrschichtigen Perzeptron
8. Die Sigmoid-Aktivierungsfunktion:Aktivierung in mehrschichtigen neuronalen Perzeptronnetzwerken
9. Wie man ein mehrschichtiges neuronales Perceptron-Netzwerk trainiert
10. Verstehen von Trainingsformeln und Backpropagation für mehrschichtige Perzeptronen
11. Neurale Netzwerkarchitektur für eine Python-Implementierung
12. So erstellen Sie ein mehrschichtiges neuronales Perceptron-Netzwerk in Python
13. Signalverarbeitung mit neuronalen Netzen:Validierung im neuronalen Netzdesign
14. Trainings-Datasets für neuronale Netze:So trainieren und validieren Sie ein neuronales Python-Netz

Was ist ein mehrschichtiges neuronales Perceptron-Netzwerk?

Der vorherige Artikel hat gezeigt, dass ein einschichtiges Perceptron einfach nicht die Leistung erbringen kann, die wir von einer modernen neuronalen Netzwerkarchitektur erwarten. Ein System, das auf linear separierbare Funktionen beschränkt ist, wird die komplexen Input-Output-Beziehungen, die in realen Signalverarbeitungsszenarien auftreten, nicht annähernd abbilden. Die Lösung ist ein mehrschichtiges Perceptron (MLP), wie dieses hier:

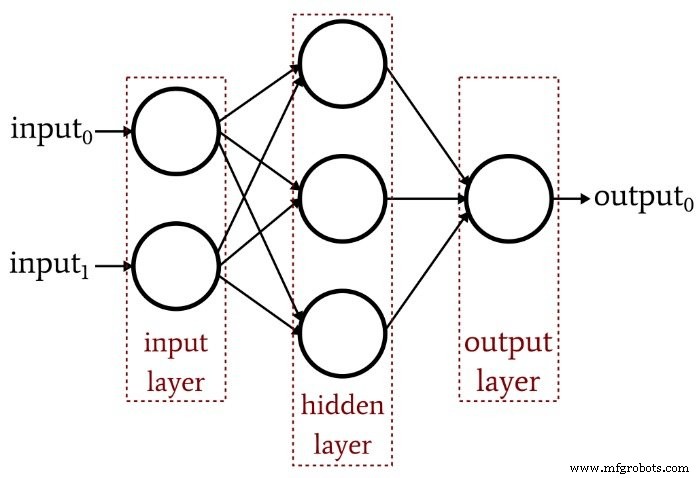
Indem wir diese versteckte Schicht hinzufügen, verwandeln wir das Netzwerk in einen „universellen Approximator“, der eine äußerst anspruchsvolle Klassifizierung erreichen kann. Aber wir müssen immer daran denken, dass der Wert eines neuronalen Netzes vollständig von der Qualität seines Trainings abhängt. Ohne reichhaltige, vielfältige Trainingsdaten und ein effektives Trainingsverfahren wird das Netzwerk nie „lernen“, wie man Eingabestichproben klassifiziert.

Warum erschwert die versteckte Schicht das Training?

Schauen wir uns die Lernregel an, mit der wir in einem früheren Artikel ein einschichtiges Perceptron trainiert haben:

\[w_{new} =w+(\alpha\times(output_{expected}-output_{berechnet})\times input)\]

Beachten Sie die implizite Annahme in dieser Gleichung:Wir aktualisieren die Gewichtungen basierend auf der beobachteten Ausgabe, damit dies funktioniert, müssen die Gewichtungen im einschichtigen Perceptron den Ausgabewert direkt beeinflussen. Es ist, als ob Sie die Temperatur des Wasserhahns auswählen, indem Sie die beiden Knöpfe für heiß und kalt drehen. Die Beziehung zwischen Gesamttemperatur und Drehknopfaktion ist ziemlich einfach, und selbst Leute, die keine Mathematik mögen, können die gewünschte Wassertemperatur finden, indem sie eine Weile an den Drehknöpfen herumfummeln.

Aber jetzt stellen Sie sich vor, dass der Wasserfluss durch die heißen und kalten Rohre auf komplexe, hochgradig nichtlineare Weise mit der Knopfposition zusammenhängt. Sie drehen den Drehknopf für Warmwasser stetig und langsam, aber die resultierende Durchflussmenge variiert unregelmäßig. Sie versuchen den Drehknopf für kaltes Wasser und er tut das gleiche. Die Einstellung auf die ideale Wassertemperatur unter diesen Bedingungen – zumal die „Leistung“ durch eine Kombination zweier verwirrender Regelbeziehungen erreicht werden muss – wäre deutlich schwieriger.

So verstehe ich das Dilemma der Hidden Layer. Die Gewichtungen, die die Eingabeknoten mit den versteckten Knoten verbinden, sind konzeptionell analog zu diesen mechanisch unberechenbaren Knöpfen – da die Gewichtungen von der Eingabe zu den versteckten Knoten keinen direkten Weg zur Ausgabeschicht haben, ist die Beziehung zwischen diesen Gewichten und der Ausgabe des Netzwerks so komplex, dass die oben gezeigte einfache Lernregel nicht effektiv ist.

Ein neues Trainingsparadigma

Da die ursprüngliche Lernregel von Perceptron nicht auf mehrschichtige Netzwerke angewendet werden kann, müssen wir unsere Trainingsstrategie überdenken. Was wir tun werden, ist den Gradientenabstieg und die Minimierung einer Fehlerfunktion zu integrieren.

Zu beachten ist, dass dieses Trainingsverfahren nicht spezifisch für mehrschichtige neuronale Netze ist. Der Gradientenabstieg stammt aus der allgemeinen Optimierungstheorie, und das Trainingsverfahren, das wir für MLPs verwenden, ist auch auf einschichtige Netzwerke anwendbar. Wie ich es verstehe, ist der Gradientenabstieg im MLP-Stil jedoch (zumindest theoretisch) für ein einschichtiges Perceptron unnötig, da die oben gezeigte einfachere Regel die Aufgabe letztendlich erledigen wird.

Das Ableiten der tatsächlichen Gewichtungs-Aktualisierungs-Gleichungen für ein MLP erfordert einige einschüchternde Mathematik, die ich an dieser Stelle nicht versuchen werde, intelligent zu erklären. Mein Ziel für den Rest dieses Artikels ist es, eine konzeptionelle Einführung in zwei Schlüsselaspekte des MLP-Trainings zu geben – den Gradientenabstieg und die Fehlerfunktion – und dann werden wir diese Diskussion im nächsten Artikel fortsetzen, indem wir eine neue Aktivierungsfunktion integrieren.

Gefälleabstieg

Wie der Name schon sagt, ist der Gradientenabstieg ein Mittel, um zum Minimum einer auf der Steigung basierenden Fehlerfunktion abzusteigen. Das Diagramm unten zeigt, wie ein Gradient uns Informationen darüber gibt, wie man Gewichte ändert – die Steigung eines Punktes auf der Fehlerfunktion sagt uns, in welche Richtung wir gehen müssen und wie weit wir vom Minimum entfernt sind.

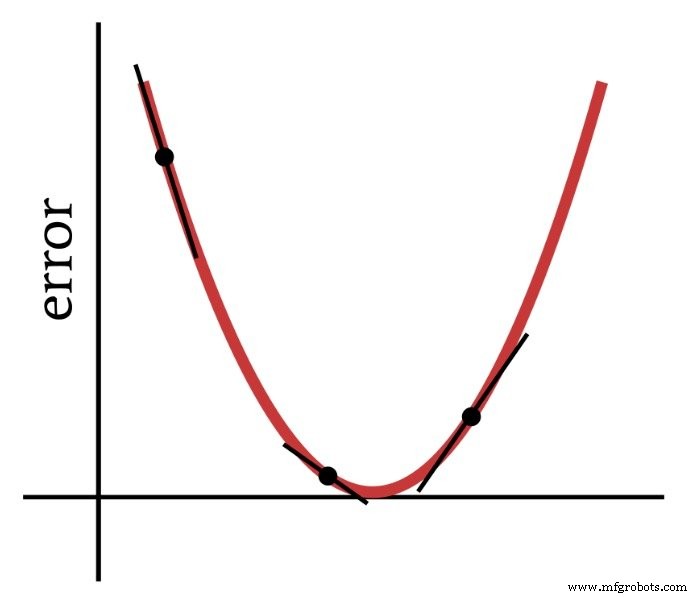
Somit ist die Ableitung der Fehlerfunktion ein wichtiges Element der Berechnungen, die wir verwenden, um ein mehrschichtiges Perzeptron zu trainieren. Eigentlich brauchen wir teilweise Derivate hier. Wenn wir einen Gradientenabstieg implementieren, machen wir jede Gewichtsänderung proportional zur Steigung der Fehlerfunktion in Bezug auf das geänderte Gewicht.

Die Fehlerfunktion (AKA Verlustfunktion)

Eine gängige Methode zur Quantifizierung des Fehlers eines neuronalen Netzes besteht darin, die Differenz zwischen dem erwarteten (oder „Ziel-“) Wert und dem berechneten Wert für jeden Ausgangsknoten zu quadrieren und dann alle diese quadrierten Differenzen zu summieren. Sie können dies „Summe of Squared Difference“ oder „Summed Squared Error“ oder vielleicht verschiedene andere Dinge nennen, und Sie werden auch die Abkürzung LMS sehen, die für Least-Mean-Square steht, da das Ziel des Trainings darin besteht, den Mittelwert zu minimieren quadratischer Fehler. Diese Fehlerfunktion (bezeichnet mit E) kann mathematisch wie folgt ausgedrückt werden:

\[E=\frac{1}{2}\sum_k(t_k-o_k)^2\]

wobei k den Bereich der Ausgabeknoten angibt, t der Zielausgabewert ist und o der berechnete Ausgabewert ist.

Schlussfolgerung

Wir haben den Grundstein für das erfolgreiche Training eines mehrschichtigen Perceptrons gelegt und werden dieses interessante Thema im nächsten Artikel weiter untersuchen.