Dualband-Fano-Resonanzen mit hohem Qualitätsfaktor, induziert durch duale Bindungszustände im Kontinuum unter Verwendung einer planaren Nanolochplatte

Einführung

Die Verbesserung der Wechselwirkung zwischen Licht und Materie, die für die Verbesserung der Leistung optischer Geräte von Bedeutung ist, kann durch die Verwendung hochwertiger (Q)-Faktor-Antworten realisiert werden [1]. Die Fano-Resonanz, die durch die asymmetrische Linienform und das scharfe Spektralprofil gekennzeichnet ist, bietet einen effektiven Ansatz zum Erreichen des hohen Q-Faktors in optischen Metamaterialien und hat große Aufmerksamkeit erfahren [2]. In den letzten zehn Jahren wurde über Fano-Resonanz in vielen nanoskaligen Oszillatorsystemen berichtet, die durch plasmonische Nanostrukturen ermöglicht werden [3, 4], bei denen die Fano-Resonanz durch die Oberflächenplasmaresonanz an der Metall-Dielektrikum-Grenzfläche angeregt wird. Obwohl metallische Metamaterialien vielversprechende Kandidaten für die Lichtmanipulation sind, leidet die Fano-Resonanz in plasmonischen Metamaterialien aufgrund der inhärenten ohmschen Verluste im Metall typischerweise unter einem niedrigen Q-Faktor im sichtbaren bis nahen Infrarot (NIR) Spektralbereich.

Auf der anderen Seite bieten volldielektrische Metamaterialien starke Mie-Typ-Resonanzen mit induzierten Verschiebungsströmen, die denen von plasmonischen Metamaterialien ähneln, weisen jedoch weniger dissipative Verluste im sichtbaren bis NIR-Bereich auf [5]. Die Energie des einfallenden Lichts kann aufgrund der Anregung der elektrischen und/oder magnetischen Dipolresonanzen in den dielektrischen Nanostrukturen stark lokalisiert werden, was die dissipativen Verluste reduziert und eine große Resonanzverstärkung sowohl der elektrischen als auch der magnetischen Felder erreicht. In den letzten Jahren haben sich gebundene Zustände im Kontinuum (BICs) als das vielversprechendste Schema herausgestellt, um Antworten mit hohem Q-Faktor in volldielektrischen Metamaterialien zu erreichen [6, 7]. BICs befinden sich innerhalb des kontinuierlichen Spektrums ausgedehnter Zustände, bleiben jedoch kontraintuitiv im Raum mit theoretisch unendlicher Lebensdauer perfekt lokalisiert [8, 9]. Obwohl BICs aufgrund der nicht strahlenden Eigenschaft nicht aus dem kontinuierlichen Spektrum beobachtbar sind, können Fano-Resonanzen mit hohem Q-Faktor erreicht werden, wenn BICs in Quasi-BICs (QBICs) umgewandelt werden [10, 11], potenzielle Anwendungen umfassen z Laser [12], optische Filter [13], nichtlineare Frequenzumwandlung [14], hochempfindliche Sensoren [15, 16] und optische Wirbelstrahlen [17].

Im Allgemeinen hängt die Bildung von BICs aufgrund ihrer interferenziellen Natur stark mit den Symmetrien (in Ebenen- und Vertikalsymmetrie) der photonischen Struktur zusammen. Insbesondere können BICs durch schrägen Einfall oder symmetriegebrochene Nanostrukturen gestört werden, und die QBICs können realisiert werden, indem der Strahlungskanal zwischen den Eigenzuständen und dem freien Raum geöffnet wird [18, 19]. Die meisten dielektrischen Nanostrukturen, die zur Anregung von QBICs mit hohem Q-Faktor verwendet werden, sind jedoch kompliziert, wie asymmetrische Nanokreuze [20], asymmetrische Nanoringe [21], asymmetrische Nanobarren [22,23,24] und asymmetrische Nanostäbe [25,26, 27,28]. Andere Nanostrukturen wie die umgeformten rechteckigen Stäbe [29, 30] haben die größeren scharfen Kanten, was es schwieriger macht, sie mit herkömmlichen lithographischen Techniken genau herzustellen, was den Q-Faktor und die Resonanzlebensdauer der Bauelemente aufgrund der Öffnung von . verringert zusätzliche undichte Kanäle [31, 32]. Darüber hinaus haben die geneigten Nanobarren [33, 34], eine andere Art von Strukturen, Schwierigkeiten bei der genauen Steuerung der Ausrichtung der Nanobarren, da die tiefen Subwellenlängenräume zwischen den Resonatoren im Nanofabrikationsprozess beibehalten werden. In Anwendungen ist es sinnvoll, BICs und Fano-Resonanzen mit hohem Q-Faktor unter Verwendung volldielektrischer Metamaterialien mit einfacheren Architekturen wie den nanostrukturierten planaren Slabs zu realisieren [35,36,37,38]. Außerdem sind mehrere Fano-Resonanzen in Anwendungen wie der Verbesserung der Mehrband-Oberwellenerzeugung [39], der Mehrkanal-Erfassung [40] und der Lichtemission [41] sehr nützlich. Daher besteht ein erheblicher Vorteil darin, mehrere Fano-Resonanzen mit hohem Q-Faktor unter Verwendung einer vergleichsweise einfachen Architektur basierend auf der Anregung von QBICs zu erreichen.

In dieser Arbeit wird eine neuartige planare Nanolochplatte (PNS) vorgeschlagen, die aus tetramerisierten Löchern besteht, um Dualband-Fano-Resonanzen mit hohem Q-Faktor zu erreichen. Durch das Schrumpfen oder Expandieren der tetramerisierten Löcher des PNS entlang der Diagonalen des Übergitters werden zwei QBICs angeregt und die Lage der beiden Fano-Resonanzen sowie deren Q-Faktoren können flexibel abgestimmt werden. Mehrfachzerlegungen im Fernfeld und Nahfeldverteilungen des Übergitters werden durchgeführt, um die Resonanzeigenschaften des PNS aufzudecken, was darauf hindeutet, dass die Dualband-Fano-Resonanzen aus den Resonanzkopplungen zwischen den elektrischen toroidalen Dipolen oder den magnetischen toroidalen Dipolen resultieren. Die Dualband-Fano-Resonanzen des PNS besitzen eine polarisationsunabhängige Eigenschaft, und sie können überlebt werden, selbst wenn die geometrischen Parameter des PNS erheblich verändert werden, wodurch es für potenzielle Anwendungen besser geeignet ist.

Methoden

Gitterstruktur und -design

Abbildung 1 zeigt die schematische Geometrie des vorgeschlagenen PNS und seine Transmissionsspektren. Das PNS besteht aus vier Nanolöchern, die mit einem Verschiebungsabstand von Δ entlang der Diagonalen des Übergitters geschrumpft (Δ < 0) oder erweitert (Δ > 0) werden können, und Δ = 0 entspricht einem einfachen Gitter mit auf die Hälfte reduzierter Periode, wobei jedes Nanoloch befindet sich in der Mitte eines Viertelbereichs des Übergitters. Die Periode und die Höhe des PNS sind bzw. H; der Radius des Nanolochs ist r . Der Brechungsindex des PNS beträgt n _s = 3,2, und der Hintergrund ist Luft mit dem Brechungsindex von n _a = 1. Abbildung 1c zeigt die Spektren des PNS als Funktion der Verschiebungsstrecke von Δ, wobei das PNS von einem normal einfallenden x . beleuchtet wird -polarisiertes Licht. Die in diesem Artikel vorgestellten Spektren sowie die elektromagnetischen Feldverteilungen des PNS werden mit der kommerziellen Finite-Elemente-Methode von COMSOL Multiphysics berechnet. Wie in Abb. 1c gezeigt, gibt es keine Fano-Resonanz für das nicht geschrumpfte PNS mit Δ = 0. Jedoch können zwei Fano-Resonanzen mit 100% Modulationstiefen (definiert als die Transmissionsunterschiede zwischen Fano-Spitzen und Fano-Einbrüchen) erhalten werden durch leichtes Schrumpfen oder Ausdehnen der Nanolöcher. Im Vergleich mit der Sendeantwort des nicht geschrumpften PNS variiert die Sendeantwort des geschrumpften PNS abrupt, während die Seitenbänder fast gleich gehalten werden.

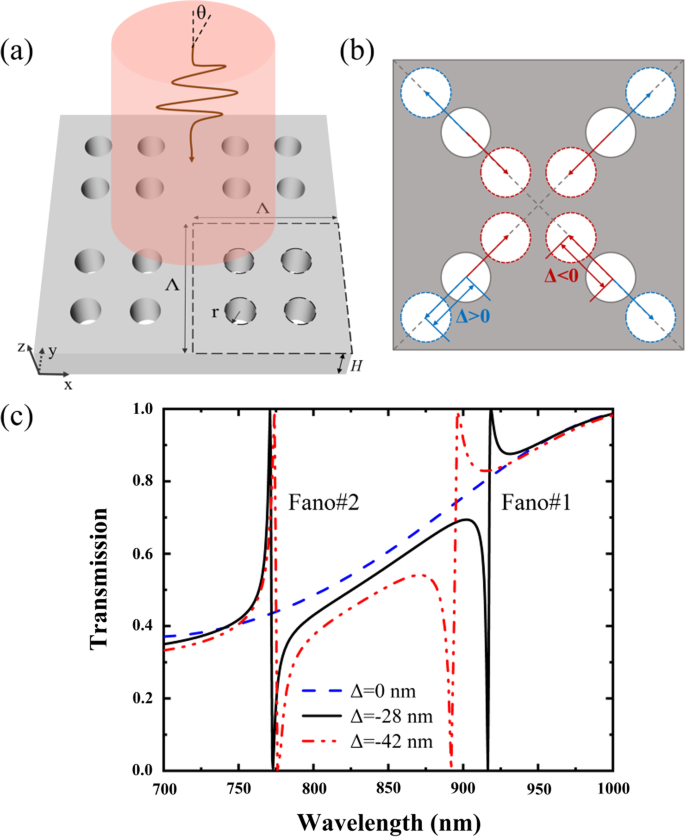
a Perspektivische Ansicht des PNS. b Vertikale Ansicht des PNS, während vier Nanolöcher entlang der Diagonalen des Übergitters schrumpfen (Δ < 0) oder sich ausdehnen (Δ > 0). c Transmissionsspektren des PNS als Funktion der Verschiebungsstrecke von Δ. Das PNS steht unter der Beleuchtung des x -polarisierte einfallende Welle mit dem Einfallswinkel von θ = 0. Die Parameter des PNS sind:Λ = 350 nm, r = 35 nm und H = 175 nm

Um die Entwicklung der Dualband-Fano-Resonanzen, die durch das Schrumpfen oder Ausdehnen der tetramerisierten Löcher entstehen, deutlich zu zeigen, ist in Abb. 2a eine 2D-Transmissionskarte des PNS als Funktion des Verschiebungsabstands von Δ gezeigt. Wie in Abb. 2a gezeigt, treten zwei BICs im interessierenden Wellenlängenbereich mit Δ = 0 auf, und ein ähnliches Phänomen von dualen BICs wurde zuvor in den Strukturen von Dual-Grating-Metamembranen [13] und Split-Ring-Resonator [21] berichtet. Im Fall von Δ ≠ 0 werden Dualband-Fano-Resonanzen realisiert, da BICs zu QBICs aufgrund der Symmetriebrechung des PNS induziert werden, dh von der Zentrosymmetrie des einfachen Gitters zur vierzähligen Rotation (C_{4 ) Symmetrie des Übergitters. Außerdem, weil der C4 Symmetrie des PNS kann aufrechterhalten werden, da die tetramerisierten Löcher entlang der Diagonalen des Übergitters geschrumpft oder erweitert werden, die Transmissionsspektren des PNS sind für denselben Absolutwert von |Δ| gleich. Im Prinzip reduziert die Schrumpfung oder Ausdehnung der tetramerisierten Löcher die Fläche der ersten Brillouin-Zone des PNS, wenn sich die Elementarzelle des PNS vom einfachen Gitter zum Übergitter ändert, und symmetriegeschützte BIC können bei senkrechtem Einfall aufgrund der Einführung von Oberflächenstörung sowie Brillouin-Zonenfaltung des PNS [42, 43]. Im Allgemeinen zeigt der Q-Faktor eines symmetriegeschützten BIC eine inverse quadratische Abhängigkeit vom Grad der Asymmetrie δ basierend auf der Störungstheorie [21]:}

$$Q_{fit} =\kappa\cdot\frac{cS}{{\omega \cdot\delta^{2} }},$$ (1)

wo ĸ ist eine Proportionalitätskonstante, S ist die Fläche eines Übergitters, ω ist die Kreisfrequenz und der Asymmetrieparameter ist \(\delta { =}\sqrt 2 \Delta /\Lambda\).

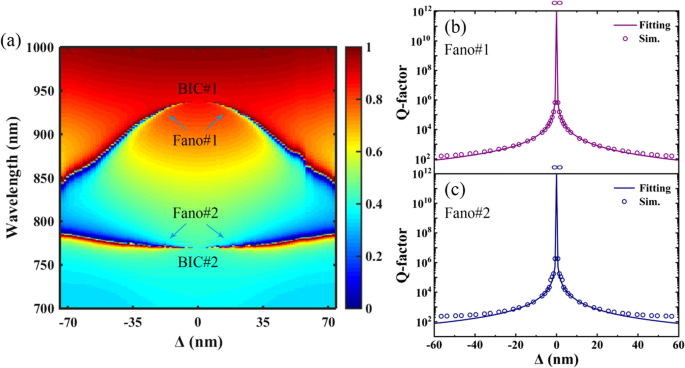
a Transmission 2D-Karte des PNS als Funktion der Verschiebungsdistanz von Δ entlang der Diagonalen des Übergitters. b und c Q-Faktor und das Anpassungsergebnis von Fano#1 bzw. Fano#2. Andere Parameter sind dieselben wie in Abb. 1c

Abbildung 2b, c zeigt den Q-Faktor und das Anpassungsergebnis von Fano#1 bzw. Fano#2. Der Q-Faktor des PNS wird als Verhältnis zwischen der Resonanzwellenlänge λ _r und seine Halbwertsbreite (FWHM) , wobei der Wellenlängenbereich zwischen der Spitze und dem Einbruch der Fano-Resonanz ist. Die Anpassungsergebnisse des PNS werden unter Verwendung von Gl. (1). Wie in Abb. 2b, c gezeigt, werden divergierende Trajektorien des PNS, bei denen die Q-Faktoren bei Δ = 0 ins Unendliche divergieren, unter Verwendung der inversen quadratischen Beziehung validiert, um die Daten anzupassen. Es können ausgezeichnete Anpassungsergebnisse erzielt werden, und die leichte Abweichung bei größerer Asymmetrie ist auf die Abweichung von der Annahme einer winzigen Störung in Gl. (1). Der wesentliche Vorteil des PNS besteht darin, dass die Lage und der Q-Faktor der Dualband-Fano-Resonanzen durch Schrumpfen oder Erweitern der tetramerisierten Löcher angepasst werden können, was die dynamische Kontrolle der Resonanzleistungen des Vielfachen mit hohem Q-Faktor erleichtert Fan-Resonanzen.

Physische Mechanismen und Interpretation

Um einen Einblick in den Ursprung der Dualband-Fano-Resonanzen durch das Schrumpfen oder Expandieren der tetramerisierten Löcher des PNS zu erhalten, zerlegen wir die Fernfeldstrahlung von BIC und Fano-Resonanz in Beiträge verschiedener Multipolkomponenten, um ihre Eigenschaften weiter zu diskutieren. Die Multipolmomente können anhand der Verschiebungsstromdichte j . berechnet werden im Übergitter des PNS [26, 44, 45]:

$${\varvec{P}} =\frac{1}{i\omega}\int {{\varvec{j}}d^{3} r} ,$$ (2) $${\varvec{M }} =\frac{1}{2c}\int {\left( {{\varvec{r}} \times {\varvec{j}}} \right)d^{3} r} ,$$ (3 ) $${\varvec{T}} =\frac{1}{10c}\int {\left[ {\left( {{\varvec{r}} \cdot {\varvec{j}}} \right) {\varvec{r}} - 2r^{2} {\varvec{j}}} \right]} d^{3} r,$$ (4) $${\varvec{Q}}_{\alpha ,\beta}^{\left( e\right)} =\frac{1}{i2\omega }\int {\left[ {r_{\alpha} j_{\beta} + r_{\beta} j_{ \alpha} - \frac{2}{3}\left( {{\varvec{r}} \cdot {\varvec{j}}} \right)}\delta_{\alpha,\beta}\right] } d^{3} r$$ (5) $${\varvec{Q}}_{\alpha,\beta}^{\left(m\right)} =\frac{1}{3c}\int {\left[ {\left( {{\varvec{r}} \times {\varvec{j}}} \right)_{\alpha} r_{\beta} + \left( {{\varvec{r} } \times {\varvec{j}}} \right)_{\beta} r_{\alpha} } \right]d^{3} r} ,$$ (6)

wobei P , M , T , Q ^{(e )} und Q ^{(m )} sind die Momente des elektrischen Dipols (ED), des magnetischen Dipols (MD), des toroidalen Dipols (TD), des elektrischen Quadrupols (EQ) bzw. des magnetischen Quadrupols (MQ); c die Lichtgeschwindigkeit im Vakuum ist und α , β = x , y , z . Hier die Ladungsdichte ρ , das normalerweise in der Definition von ED und MQ vorkommt, wurde durch Verschiebungsstromdichte j . ersetzt über die Ladungserhaltungsbeziehung von \(i\omega \rho + \nabla\cdot {\varvec{j}} =0\). Bei harmonischer Anregung ~ exp(iωt ), kann das Streuvermögen der induzierten Multipolmomente, die zur Fernfeldantwort beitragen, geschrieben werden als:

$$\begin{ausgerichtet} I &=\frac{{2\omega^{4} }}{{3c^{3} }}\left| {\varvec{P}} \right|^{2} + \frac{{2\omega^{4}}}{{3c^{3} }}\left| {\varvec{M}} \right|^{2} + \frac{{2\omega^{6}}}{{3c^{5} }}\left| {\varvec{T}} \right|^{2} + \frac{{\omega^{6}}}{{5c^{5} }}\sum\limits_{\alpha,\beta} {\left | {{\varvec{Q}}_{\alpha ,\beta}^{\left( e \right)} } \right|}^{2} \\ &\quad+ \frac{{\omega^{6} }}{{20c^{5} }}\sum\limits_{\alpha,\beta} {\left| {{\varvec{Q}}_{\alpha,\beta}^{\left(m\right)}}\right|}^{2} + {\text{o}}(\omega), \end {ausgerichtet}$$ (7)

wobei die ersten beiden Terme der herkömmlichen ED- (Ladung) und MD-Streuung entsprechen. Der dritte Term entspricht der TD-Streuung. Der vierte und fünfte Begriff stammen von EQ und MQ. Der letzte Term ist der Term höherer Ordnung, der die Multipolstreuung höherer Ordnung und die Kopplung zwischen ihnen enthält und im Allgemeinen vernachlässigt werden kann. Durch die Verwendung von Gl. (2)–(7) können die Beiträge verschiedener Multipole zum Streuvermögen des Fernfelds ermittelt werden.

Abbildung 3 zeigt die Streuleistung verschiedener Multipole des PNS für unterschiedliche Verschiebungsdistanzen von Δ, andere Parameter sind die gleichen wie in Abbildung 1c. Wie in Abb. 3a–d gezeigt, sind für das PNS mit Δ = 0 ED und MD die dominierenden Dipole und sie sind im interessierenden Wellenlängenbereich nicht resonant. Durch Verkleinern oder Aufweiten der Nanolöcher des PNS mit |Δ|≠ 0 können jedoch aufgrund der Anregungen der resonanten Dipolmoden Dualband-Fano-Resonanzen realisiert werden. Um die wichtige Rolle der resonanten Dipolmoden bei der Bildung der beobachteten Dualband-Fano-Resonanzen deutlich zu machen, zeigt Abb. 3e, f die normalisierte Streuleistung verschiedener Multipole mit Δ =  − 28 nm um Fano#1 bzw. Fano#2 . Wie in Abb. 3e gezeigt, sind die vorherrschenden Resonanzmoden ED und TD um Fano#1 herum, und Fano#1 ist die direkte Folge der Resonanzkopplung der elektrischen Ringkerndipole. Insbesondere werden ED und TD an der Resonanzspitze (918,5 nm) von Fano#1 auf eine vergleichbare Größenordnung stark verstärkt; somit kann aufgrund der destruktiven Interferenz zwischen ED und TD eine Übertragung von 100 % erreicht werden. Bei der Resonanzneigung (916,5 nm) von Fano#1 wird die Reflexion jedoch maximiert und die Transmission geht aufgrund der verstärkten Streuung von ED und TD auf Null. In ähnlicher Weise entsteht Fano#2, wie in Abb. 3f gezeigt, aus der resonanten Kopplung der magnetischen toroidalen Dipole, seine Spitze (771,1 nm) zeigt die destruktive Interferenz zwischen MD und TD an, während sein Dip (772,9 nm) mit dem verbunden ist verbesserte Streuung von MD und TD. Beachten Sie, dass aufgrund der starken Kopplung von elektrischen Ringkerndipolen oder magnetischen Ringkerndipolen die Resonanzmoden sowohl für Fano#1 als auch für Fano#2 robust sind, selbst wenn Δ variiert wird.

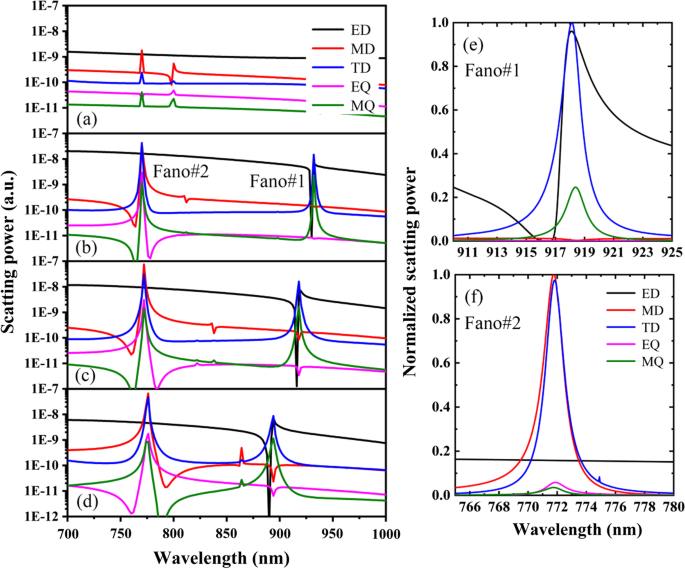
Streuleistung des kartesischen ED, MD, TD, EQ und MQ bei a Δ = 0, b Δ =  − 14 nm, c Δ =  − 28 nm und d Δ =  − 42 nm. e und f Normalisierte Streuleistung verschiedener Multipole mit Δ =  − 28 nm um Fano#1 bzw. Fano#2. Andere Parameter sind dieselben wie in Abb. 1c

Um das Übertragungsverhalten von Dualband-Fano-Resonanzen im Fernfeld mit den Anregungen induzierter Multipolmomente zu verknüpfen, sind die Verteilungen des elektromagnetischen Felds und des Verschiebungsstroms der Fano-Resonanzen des Übergitters des PNS in Abb. 4 dargestellt Abb. 4a, b, das elektrische Feld von Fano#1 ist im Übergitter des PNS mit dem Verschiebungsstrom entlang der x . gut begrenzt Achse, was einen ED-Resonanzmodus anzeigt. Darüber hinaus bildet der Verschiebungsstrom von Fano#1 zwei umgekehrte Schleifen zwischen der Mitte und den Kanten des Übergitters, und das Magnetfeld bildet eine Schleife im yz Ebene, entsprechend einer TD-Resonanzmode entlang der x Achse [44, 46]. Daher entsteht Fano#1 aus der resonanten Kopplung zwischen den ED- und TD-Modi, die mit den vorhergesagten Ergebnissen der oben erwähnten Multipolzerlegungen übereinstimmen. Tatsächlich sind aufgrund der Resonanzeigenschaften der elektrischen toroidalen Dipole von Fano#1 die Verteilungen des elektromagnetischen Felds und des Verschiebungsstroms bei der Resonanzspitze (918,5 nm), der zentralen Wellenlänge (917,5 nm) und der Resonanzneigung (916,5 nm) von Fano #1 sind fast gleich, bis auf einen kleinen Unterschied in der Feldamplitude (Zusatzdatei 1:Abb. S1). Im Fall von Fano#2, wie in Abb. 4c gezeigt, wird das elektrische Feld stark verstärkt und der Verschiebungsstrom bildet zwei umgekehrte Schleifen zwischen der Mitte des Übergitters und dem benachbarten Übergitter des PNS, was auf einen TD-Resonanzmodus entlang der hinweist z Achse. Außerdem ist das Magnetfeld von Fano#2 im Übergitter mit der Richtung entlang des y . stark lokalisiert Achse, wie in Fig. 4d gezeigt, mit einem MD-Resonanzmodus. Als Ergebnis ist Fano#2 die direkte Folge der resonanten Kopplung der magnetischen toroidalen Dipole, was mit der Vorhersage der Multipolzerlegungen des Fernfeldes des PNS übereinstimmt. Aufgrund der Kopplung der magnetischen toroidalen Dipole von Fano#2 zeigen das elektromagnetische Feld und der Verschiebungsstrom bei der Resonanzspitze (771,1 nm), der zentralen Wellenlänge (772,0 nm) und der Resonanzneigung (722,9 nm) von Fano#2 ähnliches Distributionen (Zusatzdatei 1:Abbildung S2).

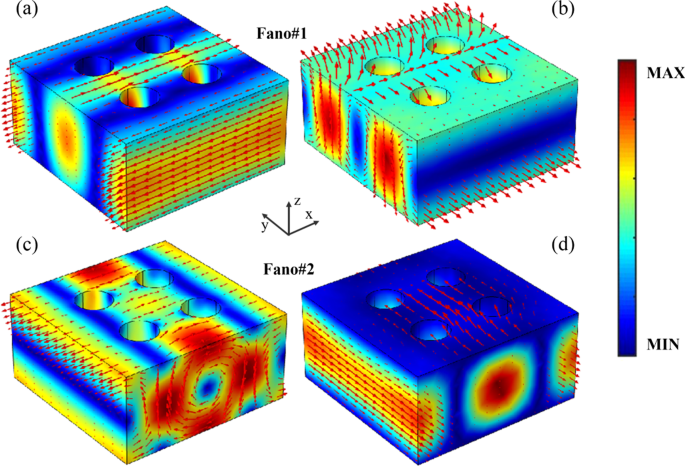
Verteilungen des elektromagnetischen Felds und des Verschiebungsstroms von Fano-Resonanzen des Übergitters des PNS, der Farbbalken repräsentiert die Feldamplitude und die roten Pfeile zeigen den Feldvektor oder Verschiebungsstromvektor an. Andere Parameter sind die gleichen wie in Abb. 1c mit Δ =  − 28 nm. a und c Verteilungen der elektrischen Feldamplitude und des Verschiebungsstromvektors von Fano#1 bzw. Fano#2. b und d Verteilungen der Magnetfeldamplitude und des Magnetfeldvektors von Fano#1 bzw. Fano#2

Ergebnisse und Diskussion

Abbildung 5 zeigt Transmissionsspektren des PNS als Funktion des Radius r des Nanolochs, und andere Parameter sind die gleichen wie in Abb. 1c mit Δ =  − 28 nm. Wie in Abb. 5a gezeigt, können Dualband-Fano-Resonanzen als r . aufrechterhalten werden variiert von 0 bis zum Maximalwert von 67,5 nm, d. h. , sind die tetramerisierten Löcher im Übergitter tangential zueinander. Die Zunahme des Nanolochradius r erhöht die Oberflächenstörungen des PNS und verringert auch seinen effektiven Brechungsindex (ERI), was zu einem erhöhten Q-Faktor und der Blauverschiebung der Fano-Resonanzen führt. Insbesondere die Resonanzposition von Fano#1 reagiert empfindlicher auf die Variation von r , und die Dualband-Fano-Resonanzen neigen dazu, zu einer Resonanzmode zu verschmelzen, wenn sich die tetramerisierten Löcher einander nähern. Wie in Abb. 5b gezeigt, ist der Anstieg von r verschiebt nicht nur die Resonanzlage der Fano-Resonanzen blau, sondern erhöht auch deren FWHMs. Als r von 25 auf 45 nm erhöht wird, sind die Resonanzpeaks von Fano#1 und Fano#2 von 936,7 nm und 793,2 nm auf 887,6 nm bzw. 743,8 nm blauverschoben; und ihre FWHMs werden von 0,8 nm und 0,6 nm auf 6,8 nm bzw. 3,1 nm erhöht. Beachten Sie den Anstieg von r verbessert auch die Modulationstiefen der Fano-Resonanzen, und 100% Modulationstiefen können als r . realisiert werden ist größer als 30 nm. Durch Auswertung der Verschiebung der Fano-Peakwellenlänge, die durch die strukturellen Parameter des PNS beeinflusst wird, wird außerdem gezeigt, dass der Nanolochradius r ist der empfindlichste Strukturparameter sowohl für Fano#1 als auch für Fano#2 (Zusatzdatei 1:Abbildung S3). Daher ist die Variation von r bietet einen effektiven Ansatz zur dynamischen Steuerung der Resonanzleistung der Dualband-Fano-Resonanzen des PNS.

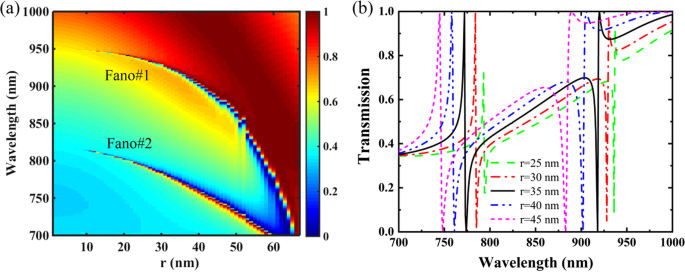
a Übertragung 2D-Karte des PNS als Funktion des Radius r des Nanolochs. b Transmissionsspektren des PNS für verschiedene Nanolochradien r . Andere Parameter sind die gleichen wie in Abb. 1c mit Δ =  − 28 nm

Abbildung 6 zeigt die Einflüsse der Symmetrie der Struktur auf die Übertragungsantworten des PNS, wobei der Radius r' von zwei Nanolöchern variiert von null bis tangential zueinander, und andere Parameter sind die gleichen wie in Fig. 1c mit Δ =  − 28 nm. Wie in Abb. 6a gezeigt, für das Übergitter mit Spiegelsymmetrie entlang der x Achse (Richtung des elektrischen Feldes des einfallenden Lichts), als Radius r ′ der beiden Nanolöcher wird vergrößert, die Resonanzorte der Dualband-Fano-Resonanzen werden aufgrund der Abnahme des ERI des PNS blauverschoben und ihre Bandbreiten werden aufgrund der erhöhten Oberflächenstörungen verbreitert. Wie in Abb. 6b gezeigt, können jedoch die beiden Fano-Resonanzen mit einer Erhöhung von r . aufrechterhalten werden ′ werden zwei zusätzliche Fano-Resonanzen als Spiegelsymmetrie des Übergitters entlang des x . auftreten Achse ist kaputt. Im Allgemeinen bricht die strukturelle Symmetrie entlang der x (y )-Achse bricht auch die Symmetrie der Mode entlang der x (y )-Achse eines periodischen Gitters, und der nicht strahlende nicht entartete Modus kann aufgrund seiner entarteten Komponente an Außenstrahlung koppeln [47]. Daher ist die Tatsache, dass die beiden zusätzlichen Fano-Resonanzen nur für die spiegelsymmetrische Struktur entlang x . vorhanden sind, Achse zeigt an, dass sie auf die gestörten nicht entarteten Modi zurückzuführen sind.

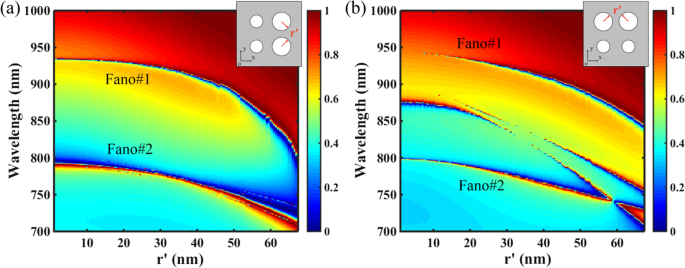
Einflüsse der Symmetrie der Struktur auf das Übertragungsverhalten des PNS. Andere Parameter sind die gleichen wie in Abb. 1c mit Δ =  − 28 nm. Die Einschubfiguren zeigen die schematische Darstellung des Übergitters des PNS. a Übertragung 2D-Karte des PNS als Funktion des Radius r ′ von zwei Nanolöchern, wobei die strukturelle Symmetrie des Übergitters entlang der x Achse wird beibehalten. b Übertragung 2D-Karte des PNS als Funktion des Radius r ′ von zwei Nanolöchern, wobei die strukturelle Symmetrie des Übergitters entlang der x Achse ist gebrochen

Wir haben außerdem die Resonanzeigenschaften des PNS unter dem Einfluss des Einfallswinkels und des Polarisationswinkels charakterisiert. Wie in Abb. 7a gezeigt, sind Dualband-Fano-Resonanzen des PNS immun gegen die Variation des Polarisationswinkels aufgrund des C₄ . symmetrische Topologie. Da sich der Polarisationswinkel von 0 auf 90° ändert, also von x -Polarisation zu y -Polarisation, Fano#1 und Fano#2 bleiben gleich. Im Fall des Einfallswinkels, wie in Fig. 7b gezeigt, ist Fano#1 zwar auch unempfindlich gegenüber der Variation des Einfallswinkels, Fano#2 wird jedoch rotverschoben, wenn der Einfallswinkel von der senkrechten Einfallsrichtung abweicht, und eine zusätzliche Fano-Resonanz (Fano#3) tritt aufgrund der Strahlungszerfallsunterdrückung des symmetriegeschützten BIC auf, wird bei außernormalem Einfall aufgehoben. Im Allgemeinen hängt diese Art der Unterdrückung des Strahlungsabfalls von BIC eng mit der destruktiven Interferenz zwischen den emittierten Strahlungsfeldern von zwei gegenläufigen Leckmoden an einer der beiden Kanten des Sperrbandes der periodischen Gitter zusammen [48]. Beachten Sie, dass aufgrund der starken Kopplung zwischen Fano#2 und Fano#3 ein schmales induziertes Transparenzfenster im Nahbereich zwischen ihnen angeregt werden kann.

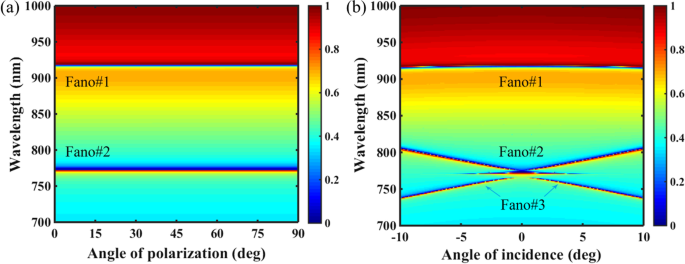
a Transmission 2D-Karte des PNS als Funktion des Polarisationswinkels. b Transmission 2D-Karte des PNS als Funktion des Einfallswinkels. Andere Parameter sind die gleichen wie in Abb. 1c mit Δ =  − 28 nm

Schließlich haben wir gezeigt, dass mehrere Fano-Resonanzen durch Erhöhung der Plattenhöhe H des PNS erhalten werden können. Abbildung 8 zeigt die 2D-Übertragungskarte des PNS als Funktionen von H für die nicht geschrumpften (Δ = 0 nm) und geschrumpften (Δ =  − 28 nm) Strukturen. Wie in Abb. 8a gezeigt, gibt es keine Fano-Resonanz außer den Fabry-Pérot-Resonanzen (F-P) für das nicht geschrumpfte PNS, wenn H variiert wird. Nach der F-P-Theorie kann die Resonanzbedingung des F-P-Hohlraums des nicht geschrumpften PNS geschrieben werden als:

$$\delta =(2\pi /\lambda )\cdot H\cdot n_{eff} + \varphi =m\pi ,$$ (8)

wo δ ist die Phasenverschiebung, λ ist die Wellenlänge im freien Raum, n _eff ist der ERI der äquivalenten homogenen Platte des PNS, φ ist die zusätzliche Phase und m ist eine ganze Zahl, die die Resonanzordnung angibt. Unter Verwendung der Effektiv-Medium-Theorie [49] kann der ERI des PNS wie folgt geschätzt werden:

$$n_{eff} =\sqrt {\frac{{\left[ {\left( {1 - f} \right)n_{a}^{2} + fn_{s}^{2} } \right] \left[ {fn_{a}^{2} + \left( {1 - f} \right)n_{s}^{2} } \right] + n_{s}^{2} }}{{2 \left[ {fn_{a}^{2} + \left( {1 - f} \right)n_{s}^{2} } \right]}}} ,$$ (9)

wo f der Füllfaktor des PNS ist und f = 1 − 4π(r /Λ) ² .

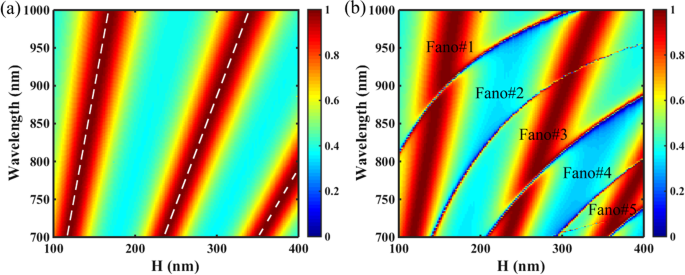
a Transmissions-2D-Karte des PNS als Funktion der Plattenhöhe H mit Δ = 0 nm, die weißen gestrichelten Linien sind die Ergebnisse des F–P-Hohlraummodells. b Transmissions-2D-Karte des PNS als Funktion der Plattenhöhe H mit Δ =  − 28 nm. Andere Parameter sind dieselben wie in Abb. 1c

Durch die Verwendung von Gl. (8) und (9) können die Orte der F-P-Resonanz des nicht geschrumpften PNS berechnet werden als λ _F–P = 2π ·H·n _eff /(mπ -φ ). In der Berechnung, obwohl die zusätzliche Phase φ kann nicht als Konstante behandelt werden, da sie offensichtlich die Phasenverschiebung δ . beeinflusst , seine Werte können mithilfe der linearen Anpassungsmethode ermittelt werden [50, 51]. Abbildung 8a zeigt die Transmissions-2D-Karte des PNS mit Δ = 0 nm, und die Ergebnisse der F-P-Theorie sind durch die weißen gestrichelten Linien gekennzeichnet. Wie in Abb. 8a gezeigt, stimmen die weißen gestrichelten Linien des F-P-Hohlraummodells mit denen der Transmissionspeaks des PNS überein, was bestätigt, dass die F-P-Resonanz die Transmission des nicht geschrumpften PNS im verstärkt Spektralbereich von Interesse. Wie in Abb. 8b gezeigt, werden jedoch für das geschrumpfte PNS mit Δ =  − 24 nm fünf Fano-Resonanzen mit hohem Q-Faktor angeregt und koexistieren mit den F-P-Resonanzen, wenn H im Bereich von 100–400 nm . variiert wird , sind die Fano-Resonanzen so stark, dass sie die FP-Resonanzen im Kreuzungsbereich zwischen den Fano- und FP-Resonanzen aufspalten. Nach der Slab-Wellenleiter-Theorie sorgt die Zunahme der Dicke der photonischen Kristallplatte für mehr in der Struktur begrenzte Leckmoden [32, 52]; somit kann die Anzahl der Fano-Resonanzen erhöht werden, indem lediglich die Dicke des PNS erhöht wird. Beachten Sie, dass die Verschiebung der tetramerisierten Löcher den ERI des PNS nicht ändert, daher werden die Positionen der FP-Resonanzen sowohl für die nicht geschrumpften als auch für die geschrumpften Strukturen fast gleich gehalten.

Schlussfolgerungen

Dualband-Fano-Resonanzen mit hohem Q-Faktor können durch die Verwendung einer vergleichsweise einfachen Architektur von PNS basierend auf der Anregung von Dual-QBICs realisiert werden. By shrinking or expanding four nanoholes of the PNS along the diagonals of the superlattice, two symmetry-protected BICs can be transformed to dual-band Fano resonances and their locations as well as their Q-factors can be flexibly tuned. The dual-band Fano resonances of the PNS are resulted from the resonant couplings between the electric toroidal dipoles or the magnetic toroidal dipoles, and their correlations between the far-field multiple decompositions and the near-field distributions of the superlattice are verified. The dual-band Fano resonances of the PNS possess polarization-independent feature, and their high-Q-factor features are robust to the variations of the geometric parameters. By increasing the height of the PNS, the number of high-Q-factor Fano resonances can be improved as more leaky modes can be supported by the structure. Our results give more tuning freedoms for the realization of high-Q-factor resonators with better performances, which may provide a further step in the development of lasing, sensing and nonlinear photonics.

Verfügbarkeit von Daten und Materialien

Die in der aktuellen Studie verwendeten und/oder analysierten Datensätze sind auf begründete Anfrage beim entsprechenden Autor erhältlich.

Abkürzungen

Q-factor:

Quality factor

PNS:

Planar nanohole slab

BICs:

Bound states in the continuum

NIR:

Near-infrared

QBICs:

Quasi-BICs

FWHM:

Full width at half maximum

ED:

Electric dipole

MD:

Magnetic dipole

TD:

Toroidal dipole

EQ:

Electric quadrupole

MQ:

Magnetic quadrupole

ERI:

Effective refractive index

F–P:

Fabry–Pérot