Verfahren zur Messung von Bewegungsparametern mit mehreren Freiheitsgraden basierend auf Polydimethylsiloxan-Kreuzkopplungs-Beugungsgittern

Hintergrund

Bewegungsparameter mit mehreren Freiheitsgraden können genaue Positions- und Lageinformationen über ein bestimmtes Ziel liefern, die für große Strukturen in Anwendungen wie der Kontrolle der Lagestabilität von Flugzeugen, der Zielstabilität von Kanonensondensystemen, Roboterarmen weit verbreitet sind Bewegung, Ausrichtung von Präzisionsteilen und Werkstückpositionierung für die industrielle Bearbeitung [1,2,3].

Daher wurden hochpräzise Erkennungsmethoden verwendet, um Informationen mit mehreren Freiheitsgraden (z. B. Geradheit, Neigung und Ablenkwinkel) über Ziele zu erfassen, und diese Methoden erforderten Hochleistungssensoren, einschließlich der Eigenschaften der Hochgeschwindigkeitserkennung , Synchronisation, hohe Messgenauigkeit und in Echtzeit. Diese Methoden wurden häufig in der Luft- und Raumfahrt, in unbemannten Luftfahrzeugen, in der Präzisionsfertigung und in optischen Ausrichtungsanwendungen eingesetzt [4,5,6].

Die Methode der präzisen Echtzeitmessung und Entkopplung der dynamischen Bewegungsinformationen mit mehreren Freiheitsgraden waren die Schlüsselelemente zur Bestimmung der Trägerlagestabilität. Hsieh [7] schlug ein dreidimensionales Detektions-Array vor, das drei Modulgruppen zum Erfassen der unterschiedlichen Freiheitsgrade verwendet, wobei verschiedene Sensormodule zum Messen der unterschiedlichen Positionsinformationen verwendet werden und ein Algorithmus verwendet wird, um die Winkel- und Multi- Informationen zu Freiheitsgraden. Liu [8] stellte ein Messverfahren für Bewegungsparameter mit mehreren Freiheitsgraden vor, das auf der Änderung des relativen Winkels zwischen zwei Montagegittern basiert, um die Informationsmessungen durchzuführen. Der obige Ansatz war jedoch anfällig für Fehler bei der Montage von zwei oder mehr Sensorelementen und die Komplexität der Kopplungsberechnungen, und seine Genauigkeit hängt auch vom hochpräzisen Instrumentensystem ab.

Mit der Entwicklung der Mikro-Nano-Fertigungstechnologie, der Nanotechnologie und der Nanomaterialien haben die Forscher die Bewegungsparameter-Erkennungsmethoden mit mehreren Freiheitsgraden basierend auf der Einzelchip-Implementierung unter dem Gesichtspunkt der Miniaturisierung und kostengünstigen Anwendung in der Bereichen Nanomaterialien, optische Materialien und Nanogeräte. Tana [9] berichtete über einen Bewegungsparameter-Erfassungsalgorithmus mit mehreren Freiheitsgraden mit einem nicht beugenden Strahl, der auf einer tragbaren miniaturisierten Prismenstruktur basiert, die Messfehler minimieren könnte. Unser Team hat ein vektorielles Dehnungsmessstreifen-Verfahren vorgestellt, das auf einem einzelnen Sensorelement basiert, das auf vektorielle Oberflächendehnungsmessungen mit mehrachsigen integrierten mechanischen Sensoren angewendet werden kann und die Grundlage für die Forschung in diesem Artikel bildet [8, 10].

In dieser Arbeit wurde ein Vektorverschiebungs- und Winkelmessverfahren mit mehreren Freiheitsgraden basierend auf einem einzigen Element demonstriert; Dieses Element wurde unter Verwendung einer Sauerstoffplasma-Verarbeitungstechnologie hergestellt, um eine optische orthogonale Gradienten-Gitterstruktur auf beiden Seiten eines Polydimethylsiloxan-(PDMS)-Substrats zu bilden, das in eine Ellipsenform vorgebogen war. Diese gekreuzten optischen Gitter können bewirken, dass ein eingegebener Laserstrahl in ein zweidimensionales Punktarray gebeugt wird. Die Ortsinformationen des Beugungsflecks können verwendet werden, um den Einfallsstrahlwinkel zu erhalten, der durch den Ortsalgorithmus in Echtzeit berechnet wird. Basierend auf dieser Methode und einem 480 × 640 Pixel großen Charge-Coupled-Device (CCD) betrugen die Messauflösungen der Verschiebung und des Ablenkwinkels 0,18 μm bzw. 0,0075 rad. Darüber hinaus können CCDs mit höheren Pixeln die Messauflösung der Verschiebung und des Ablenkwinkels auf Sub-Nanometer- bzw. Mikroradian-Niveaus verbessern. Schließlich wurde die dynamische Position eines schwebenden Drehflüglers mit dem vorgeschlagenen Verfahren in Echtzeit verfolgt; Die gewonnenen Informationen können verwendet werden, um die Position des Flugzeugs zu korrigieren und beweisen eine neue Methode zur Stabilisierung von Flugzeugen am Himmel.

Experimentell

Polydimethylsiloxan (PDMS)-Vorbereitung

Das PDMS (Sylgard 184) wurde von Dow Corning bezogen. PDMS (10:1)-Membranen wurden durch Schleuderbeschichtung auf Siliziumwafern hergestellt und unmittelbar nach dem Schleudern bei Temperaturen von weniger als 80 °C für 2 h ausgehärtet. PDMS-Substrate mit einer Dicke von 600 μm wurden durch Steuerung der Schleudergeschwindigkeit hergestellt.

Doppelte orthogonale Gittervorbereitung

Entsprechend den experimentellen Vorgaben wurden die PDMS-Filme mit einer Fläche von 3 × 3 cm ² . hergestellt . Die PDMS-Filme wurden dann mit Hilfe eines selbstgebauten Übersetzungstisches gegenüber dem Original um das 1,5-fache in X-Richtung vorgespannt. Zerknittertes SiO _x Schichten wurden dann auf dem O₂ . gebildet plasmabehandeltes vorgespanntes PDMS-Substrat (IoN Wave 10, PVA-TePla, Deutschland) unter Bedingungen einer Sauerstoffflussrate von 30 sccm und einer Oxidationszeit von 40 s. Auf der Oberfläche des PDMS-Substrats wurden nach dem Entspannen der Vorspannung gleichmäßige und geordnete Nanogitterstrukturen gebildet. Wie in Fig. 1a gezeigt, wurde dieser Vorgang auf der anderen Seite des PDMS-Substrats mit einem Winkelunterschied von 90° wiederholt, um die orthogonalen Gitterstrukturen auf beiden Seiten des PDMS-Substrats zu bilden.

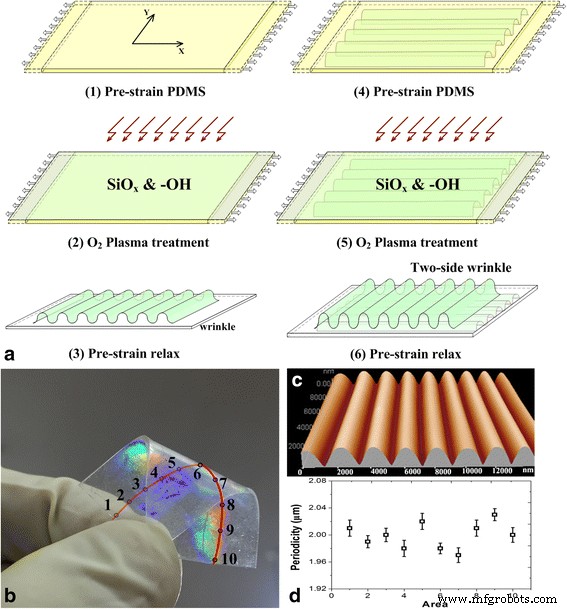
Herstellungsprozess und morphologische Charakterisierungen von PDMS-doppelten optischen Gittern. a Herstellung eines optischen Doppelgitters. b Die optischen Bilder des Gitters. c Rasterkraftmikroskopische Aufnahme des Gitters. d Die Gleichmäßigkeit der Periodizität für die Proben

Erstellen einer Testplattform

Das Bewegungswinkelsensorsystem mit vier Freiheitsgraden umfasst eine Laserlichtquelle, eine Winkel- und Verschiebungsplattformbaugruppe, einen Probenhalter, einen Bildschirm, eine CCD-Kamera und einen Computer. Wie in Abb. 2a gezeigt, wurde eine He-Ne-Laserlichtquelle (Laserwellenlänge 680 nm) in der Winkel- und Verschiebungsplattformbaugruppe installiert, die aus einer elektrischen Drehplattform und einem manuellen dreidimensionalen Einstellrahmen (Beijing Zolix Instrument Co., Ltd .) bestand .). Die Plattform hat eine Rotationsgenauigkeit von 0,1° und eine Verschiebungsgenauigkeit von 2 μm. Dieses gekreuzte optische Gitter kann bewirken, dass der Laserstrahl in ein zweidimensionales Punktarray gebeugt wird. Eine komplementäre Metall-Oxid-Halbleiter-Kamera (CMOS) mit 480 × 640 Pixeln wurde verwendet, um mithilfe von MATLAB-Bildverarbeitungsalgorithmen in Echtzeit ein Bild des zweidimensionalen Punktarrays aufzunehmen, das verwendet wurde, um jede Beugungspunktposition zu extrahieren und dann zu berechnen die x- und y -Achsenverschiebungen und die Winkelinformationen. Eine Testplattform in Form eines Vier-Rotor-Flugzeugs (Typhoon Q500, Yuneec Electric Aviation) wurde bereitgestellt. Und Informationen über vier Freiheitsgrade wurden erfasst, um die Schwebehaltung in Innenräumen zu erhalten.

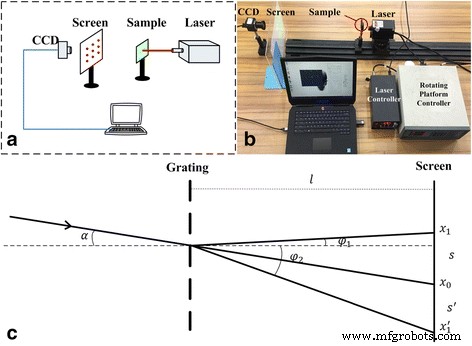
Das Prinzip und Testsystem für den Bewegungsparameter MODF. a Systemdiagramm. b Systemkonfiguration. c Prüfprinzip von Weg und Winkel

Analyse und Diskussion

Orthogonale PDMS-Gittercharakterisierung

Der Herstellungsprozess wurde wie in Abb. 1a gezeigt. Die hydrophile Oberflächenmodifizierung von PDMS verwendet die Sauerstoffplasmatechnologie. A SiO _x Schicht und hydrophile Gruppen (z. B. –OH) wurden so auf den vorgebogenen PDMS-Substraten durch das Sauerstoffplasma gebildet. Wenn die Vorspannung im PDMS-Substrat einen kritischen Wert überschreitet, bildeten sich nach der Entspannung der Vorspannung Gitterstrukturen auf der Oberfläche von PDMS [11, 12]. Die Periodizität der Gitter wurde durch Abstimmung der angewandten Vorbiege- und Plasmabedingungen erreicht und kann in unseren bisherigen Arbeiten berechnet werden. Wie in Abb. 1c gezeigt, wurden die Topographien der Mikro-/Nanogitter durch Rasterkraftmikroskopie (AFM) (CSPM5500; Benyuan Co.) charakterisiert. Wie in Abb. 1b, d gezeigt, wurden 10 Bereiche entlang der Mittellinie auf der einen Seite der Probe ausgewählt, um die Periodizität und die Gleichmäßigkeit von Gitterstrukturen zu untersuchen. Die entsprechende Periodizität der Gitter von 10 Bereichen war einheitlich und hatte eine Periode von (2 ± 0,05) μm über die gesamte Probenoberfläche.

Beugungsgitter zur Charakterisierung von Positions- und Winkelbewegungsparametern

Der Laserstrahl wandert an der Probe (mit dem Gitter) vorbei, um gemäß der Fraunhofer-Beugungstheorie [13] in eine Lichtfleckmatrix zu beugen. Die Position des Beugungsflecks stand in direktem Zusammenhang mit der Position und dem Winkel des einfallenden Strahls, und somit können die Positionsinformationen des einfallenden Strahls durch die Ortsinformationen der Beugungsflecken erfasst werden.

Abbildung 2 zeigt die sich bewegende und rotierende Plattform, um die Positionierung und die entsprechenden Beugungsflecken des einfallenden Strahls zu verfolgen. Gemäß der Fraunhofer-Beugungstheorie kann die Beziehung zwischen dem einfallenden Strahl, dem gebeugten Strahl und der Wellenlänge, wenn das Beugungsgitter und der Bildschirmabstand festgelegt sind, wie folgt ausgedrückt werden:

Hier, λ war die Wellenlänge des einfallenden Strahls, d war die Periode des Gitters, α war der Einfallswinkel, φ war der Beugungswinkel und m war die Gitterbeugungsordnung.

Wenn der Einfallswinkel α ungleich 0, „+“ bedeutet dann, dass der Beugungsstrahl und der einfallende Strahl auf derselben Seite der Gitternormalen verteilt sind, während „–“ anzeigt, dass der Beugungsstrahl und der einfallende Strahl auf zwei Seiten der Normalen existieren. Bei einem bestimmten Einfallswinkel waren die Abstände zwischen den Beugungspunkten erster Ordnung und den Beugungspunkten nullter Ordnung auf dem Bildschirm nicht gleich. Daher kann sich der Abstand zwischen den Punkten mit dem Einfallswinkel ändern. Der Winkel des einfallenden Strahls kann durch Berechnung der Position des Beugungslichtflecks quantitativ berechnet werden. Gleichzeitig bewirkt der bewegliche Ort des einfallenden Strahls eine Bewegung des Beugungspunkts nullter Ordnung. Die Positionsinformationen des einfallenden Strahls können durch die Positionsinformationen des Beugungsstrahlpunkts nullter Ordnung berechnet werden.

Abbildung 2c zeigt eine einzelne Richtung des Gitterbeugungsdiagramms, wobei x ₀ war die erste Ordnung von Beugungsflecken und x ₁ und \( {x}_1^{\hbox{'}} \) geben die zweite Ordnung von Beugungsflecken an. Aus Abb. 2c, s und s ’ waren der Abstand zwischen den Beugungsflecken erster und zweiter Ordnung, die wie folgt ausgedrückt wurden:

Aus der Gl. (1):

Aus dem Obigen kann das Korrelationsmodell zwischen dem Strahleinfallswinkel und dem Beugungsfleckabstand erhalten werden als:

Orthogonale Beugungsgitter-basierte Bewegungsparametererkennung und -charakterisierung mit mehreren Freiheitsgraden

Ein Laserstrahl, der ein optisches Einrichtungsgitter passiert, kann die einzelnen Beugungsflecken bilden. Die orthogonal orientierte kann gebildet werden, wenn der Laserstrahl die orthogonalen Gitter auf den beiden Seiten des PDMS-Substrats passiert. Ein eindimensionaler Gitterbeugungsstrahl wird gebildet, wenn ein Lichtstrahl entlang der Richtung des Gitters auf einer Seite auf dem Bildschirm durchgelassen wird und die Abmessungen in x . eingestellt wurden -Achse. Ein eindimensionaler Gitterbeugungsstrahl wurde dann orthogonal zum x . gebildet -Achse, wenn ein Lichtstrahl entlang der Richtung des Gitters auf der anderen Seite auf dem Bildschirm passiert und die Dimension dann im y . eingestellt wurde -Achse. Auf dem Bildschirm wurde ein zweidimensionales Beugungspunktarray gebildet, wie in Abb. 3b gezeigt.

Der MODF-Bewegungsparameter hängt von der Bewegung der Beugungsflecken ab. a Durch das Einrichtungsgitter wurden eindimensionale Beugungsflecken erzeugt. b Ein zweidimensionales Punktarray wurde durch das optische Doppelkreuzgitter erzeugt. c Die Bewegung des Punktarrays wurde durch die Bewegung der Laserquelle gesteuert. d Die Spaltbewegung zwischen dem Punktarray wurde als Einfallswinkel des Laserstrahls gesteuert

Wenn die Position eines Laserstrahls geändert wurde, zeigt die Position des Beugungslichtflecks nullter Ordnung eine entsprechende Bewegung, und die Position der Beugungs-Bitmap ändert sich entsprechend basierend auf der Fraunhofer-Beugungstheorie. Die Position des einfallenden Strahls kann basierend auf der Richtung der Gitterbewegung direkt berechnet und dann die Positionsinformationen des Lichtstrahls entlang des x- . erfasst werden und y -Achse. Wie in Fig. 3c gezeigt, kann die erste Ordnung der Beugungspunktposition die Lichtverschiebung aufgrund der Kopplungseffekte der Verschiebung und der Ablenkung nicht genau berechnen. Außerdem war die Position des Beugungspunkts nullter Ordnung nur auf den Ort der Quelle bezogen. Daher wäre es genauer, die Beugungspunktverschiebung nullter Ordnung zu verwenden, um die Position der Lichtquelle zu berechnen. Wie in Fig. 3d gezeigt, sind die Ablenkwinkelinformationen der einfallenden Lichtstrahlen entlang der x -Achse und das y -Achse kann durch den Abstand zwischen Lichtflecken auf dem x . berechnet werden -Achse und das y -Achse basierend auf dem entsprechenden Modell zwischen dem Winkel und der Änderung des Flecks.

Jedoch hängt die Beschränkung des Grundes der Verschiebung von Beugungsflecken vom Einfallswinkel und dem Abstand zwischen dem Gitter und dem Schirm basierend auf der Gl. (1). In unseren Arbeiten wurde das Gitter mit dem Bildschirm fixiert, was bedeutet, dass die Abstandsvariation zwischen dem Gitter und dem Bildschirm Null war. Es gab keine Verschiebung der Beugungsflecken, wenn sich die Laserquelle entlang des z . bewegte -Achse. Auch wenn sich die Laserquelle entlang der z . drehte -Achse war die Variation des Einfallswinkels null, was zu einer Nichtverschiebung der Beugungsflecken führen würde.

In unseren Experimenten ist die Winkeländerung (Δθ _x ) entlang des x -Achse kann anhand der Spaltenabstände berechnet werden (s _x ,\( {s}_x^{\hbox{'}} \)) der Beugungsflecken und die Winkeländerung (∆θ _y ) entlang der y -Achse kann anhand der Spaltenabstände berechnet werden (s _y ,\({s}_y^{\prime}\)) der Beugungsflecken. Die Portfolioplattform wurde angepasst, um den Standort der Lichtquelle zu ändern, und dann wurden die Kamerabilder alle 0,02 s von der MATLAB-Software erfasst, um die Position der Beugungsflecken zum Vergleich mit früheren Werten zu extrahieren, die verwendet wurden, um die Verschiebungen der Fleckanordnung auf dem x -Achse und das y -axis und die Änderungen des Spalten- und Zeilenabstands des Arrays.

Basierend auf dem Algorithmus kann die Verschiebung des Spot-Arrays analysiert werden, indem das Bild vor und nach der Bewegung bearbeitet wird, um das ∆x . zu berechnen ,∆y , θ _x , und θ _y . Da der Laserpunkt mehrere Pixel im Bild enthält und seine Energie der Gaußschen Verteilung entsprach, wurde das Anpassungsverfahren der Gaußschen Verteilung verwendet, um das Hintergrundrauschen aus dem Bild zu entfernen, um die Position des Zentrums des Laserpunkts genau zu extrahieren. Die Gaußsche Funktion des Laserspots wird wie folgt ausgedrückt:

Hier, ich (x , y ) war die Spotintensität und H war die Amplitude, (x ₀ , y ₀ ) waren die Koordinaten des Lichtfleckzentrums und σ ₁ , σ ₂ waren die Standardabweichungen der x -Achse und das y -Achse bzw.

Ein Logarithmus kann auf beide Seiten der obigen Gleichung angewendet werden, um die Punktzentrumsposition zu erhalten, die wie folgt ausgedrückt werden kann:

Hier, a , b , c , und d waren die Polynomkoeffizienten, die durch Gaußsche Anpassung aller Pixel im Fleck erhalten wurden.

Die Abstandsänderungen zwischen zwei Beugungsflecken wurden durch zwei Bilder vor und nach der Bewegung berechnet. Und der Zentrumsfleck der Beugungsflecken wurde als das System der Koordinatenzentren vor der Bewegung festgelegt:das absolute Verschiebungs- und das relative Verschiebungs-Koordinatensystem des Lichtflecks. Das absolute Verschiebungskoordinatensystem des Beugungslichtflecks nahm einen Ruheschirm als Referenz. Die Bewegungsinformationen (Δx ,Δy ) des Gitters in beiden Bildschirmen kann durch die nullte Ordnung der Beugungspunktkoordinate (d. h. die Mittelposition) berechnet werden. Das relative Verschiebungskoordinatensystem für den Lichtfleck verwendet den Beugungsfleck nullter Ordnung als Referenz, der verwendet werden kann, um die Änderungen des Fleck-Array-Abstands (S _x ) und der Zeilenabstand (S _y ).

Abbildung 4 zeigt die Charakterisierung der vier Freiheitsgrade. Wenn der Laserstrahl entlang des x . mähte -Achse gab es eine entsprechende Bewegung des Beugungsgitters im x -Achse, aber die Verschiebung war im y . ungefähr null -Achse. Die Verschiebungsempfindlichkeit betrug etwa 5,4 Pixel/μm. Diese Methode kann verwendet werden, um die Positionsinformationen für die Lichtquelle entlang der Achse mit hoher Genauigkeit zu berechnen, wie in Abb. 4a gezeigt.

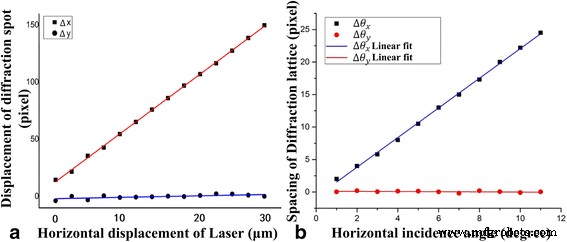
Charakterisierung von vier Freiheitsgraden. a Die Verschiebung der Laserquelle hängt von der Verschiebung der Beugungsflecken ab. b Der Einfallswinkel der Laserquelle hängt von der Lücke zwischen den Beugungsflecken ab

Wenn sich der Laser um einen kleinen Winkel entlang der x . drehte -Achse, gab es eine entsprechende Abstandsänderung des Beugungs-Spot-Array-Reihenabstands und der Spot-Array-Spaltenabstand war null. Die Verschiebungsempfindlichkeit betrug etwa 2,3 Pixel pro Winkel (/°). Inzwischen beträgt der Messbereich des Winkels theoretisch etwa 9,8°, berechnet nach den Gl. (1)–(5) als Abstand s = 0. Wenn die Zuordnung zu Beugungsflecken erster Ordnung mit der Beugungsflecken nullter Ordnung übereinstimmt, wenn der Einfallswinkel erhöht wird, wäre die Abstandsänderung der Beugungsflecken null (s = 0). Diese Methode kann verwendet werden, um die Winkelinformationen der Lichtquelle entlang des x . zu erhalten -Achse. Die Positions- und Winkelinformationen können auch mit dieser Methode abgerufen werden.

Die Erkennungsauflösung eines Pixels hängt vom Algorithmus ab, der auf der MATLAB-Software basiert. Wie oben berechnet, hat die Methode eine Verschiebungsempfindlichkeit von 5,4 Pixel/μm, was bedeutet, dass die Auflösung 0,18 μm betrug. Für die Verschiebungsempfindlichkeit von 2,3 Pixeln/° , es war eine Auflösung von 0,0075 rad. Dies zeigt, dass basierend auf der hier vorgestellten Methode und der CCD-Auflösung die Auflösungen der Verschiebung und des Winkels 0,18 μm bzw. 0,0075 rad betrugen. Das 480 × 640 Pixel-CCD wurde verwendet, um das Bild des zweidimensionalen Punktarrays in Echtzeit zu erfassen. Darüber hinaus könnten eine höhere Pixel-CCD und eine Optimierung des Lichtwegs die Auflösungen der Verschiebung und des Ablenkwinkels bis in Sub-Nanometer- bzw. Mikroradiant-Skalen verbessern.

Charakterisierung der Rotorbewegungsparameter von schwebenden Flugzeugen

Ein Drehflügler war eine Art ziviles unbemanntes Flugzeugsystem mit geringer Präzision, das in der Luft-, Modellflugzeug- und Navigationsbranche weit verbreitet war. Die Stabilitätskontrolle eines Drehflüglers repräsentiert einen Mikrokosmos einer unbemannten Kampfplattform. Um eine hochpräzise Flugsteuerung zu realisieren, war der wichtigste Aspekt die stetige Kontrolle der Fluglage und Position des Flugzeugs. Und der Kernaspekt war die Dekodierung der hochpräzisen Schwebelage- und Positionsinformationen in Echtzeit, so dass die genauen Bewegungsparameterinformationen mit vier Freiheitsgraden über das Schweben zu einem wesentlichen Vorteil werden.

In unserem Experiment, basierend auf einem kreuzgekoppelten Beugungsgitter, wurde ein Messverfahren vorgestellt, um die Fluglageinformationen des Flugzeugs mit vier Freiheitsgraden in Echtzeit zu erhalten. Zuerst wurde ein Vier-Rotor-Flugzeug verwendet, um die Plattform zu ersetzen, die aus der Position und Haltung eines Vier-Freiheits-Testsystems bestand, das auf einem Doppelgitter zum Einrichten der Vier-Grad-of- basierte -Freiheitslage-Testsystem für Vier-Rotor-Flugzeuge. Im Testsystem wurde ein kleiner Laserpointer als Lichtquelle in der Mitte eines Vier-Rotor-Flugzeugs befestigt und strahlt die Laserstrahlen senkrecht nach unten. Eine Probe mit dem Doppelgitter, einem Bildschirm und einer Kamera drehen sich um die Mitte der optischen Achse. Dieses gekreuzte optische Gitter kann bewirken, dass der Laserstrahl in ein zweidimensionales Punktarray gebeugt wird. In den Experimenten wurde die Kamera verwendet, um das Bild vom Bildschirm zu erfassen und Bilder in Echtzeit an den Computer zu übertragen, um die Verschiebungsinformationen durch die MATLAB-Software zu berechnen.

Um schnelle, genaue und Echtzeitmessungen der Flugsignale zu erzielen, schwebte ein Flugzeug mit vier Rotoren in der Luft und verfolgte das Positionssignal schnell, das 4 s lang aufrechterhalten wurde. Informationen zu den axialen Verschiebungen entlang der x -Achse und das y -Achse für Flugzeuge mit vier Rotoren wurden in einer Zeit von 4 s erhalten, wie in Fig. 5c gezeigt. Auf der Grundlage eines ebenen Koordinatensystems (d. h. eines x -Achse und ein y -Achse), das x und y Werte werden in diese Koordinatenpunkte umgewandelt. Die 200 Positionierungsergebnisse in 4 s bedeuten, dass ein Punkt in 0,02 s erfasst wurde. Dies entspricht der Verwendung der Tracking-Methode für das Flugzeug alle 0,02 s in Echtzeit, um seinen Standort und seine Position zu bestimmen. Das Flugzeug hat eine maximale Verschiebung von 2,1 mm im x -Achse und maximale Verschiebung von 2,3 mm im y -Achse, gemäß dem Algorithmus.

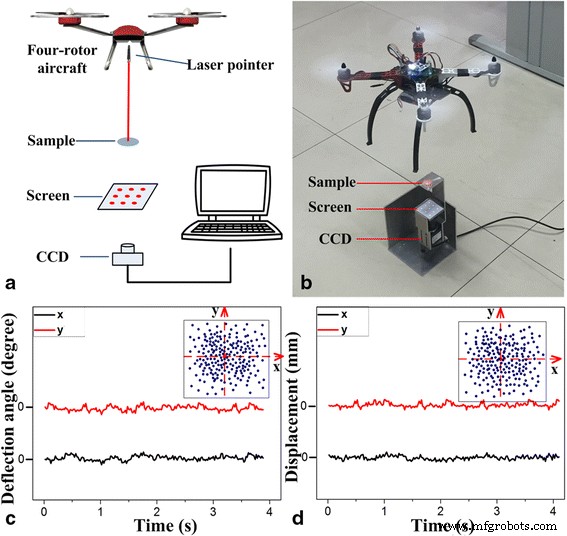
Charakterisierungen der Haltung von Vier-Rotor-Fahrzeugen. a Systemdiagramm. b Einrichtung des Systems. c Ablenkungswinkel von Drehflüglern. d Verdrängung von Drehflüglern

Außerdem wurden die Nickwinkel- und Rollwinkelinformationen für das Flugzeug durch den obigen Algorithmus und das obige Datenverarbeitungsverfahren berechnet. Wie im Einschub von Fig. 5d gezeigt, lieferte das Drehwinkel-Punktdiagramm des Vier-Rotor-Flugzeugs genaue Winkelinformationen für das Flugzeug durch Verfolgung in Echtzeit alle 0,02 s. Es stellte sich heraus, dass das Flugzeug eine maximale Winkelabweichung von 1° im x . hat -Achse und die y- Achse. Diese Methode kann somit die Informationen zu den vier Freiheitsgraden für Flugzeuge berechnen, die die genauen Positions- und Winkelsignale innerhalb von 0,02 s an das Flugsteuerungssystem zurückgeben können, um die Stabilität des Flugzeugs zu verbessern.

Schlussfolgerungen

Zusammenfassend wurde eine einfache herstellbare Technologie demonstriert, um die orthogonale optische Gitterstruktur mit einer Periodizität von 2 μm auf den beiden Seiten des PDMS-Substrats herzustellen. Basierend auf der orthogonalen optischen Gitterstruktur wurde ein Verfahren zum Identifizieren der Strahlposition und einer Winkelbewegungsparameterinformation unter Verwendung der Beugungslichtfleckpositionsinformation basierend auf dem Fraunhofer-Beugungseffekt untersucht. Ein 480 × 640-Pixel-CCD wurde verwendet, um Bilder des zweidimensionalen Punktarrays in Echtzeit zu erfassen. Die Ergebnisse zeigen, dass bei Verwendung dieser Methode und des oben beschriebenen CCD die Auflösungen der Verschiebung und des Ablenkwinkels 0,18 μm bzw. 0,0075 rad betrugen. Darüber hinaus können mit dem CCD mit höheren Pixeln die Auflösungen der Verschiebung und des Ablenkwinkels bis auf Sub-Nanometer- bzw. Mikro-Radiant-Skalen verbessert werden. Diese Methode kann verwendet werden, um genaue Schwebepositionen und Winkelinformationen für Rotorflugzeuge in Echtzeit mit hoher Genauigkeit alle 0,02 s zu erkennen. Die Informationen können an die Steuerung des Flugsystems für unbemannte Fluggeräte in der Luft zurückgegeben werden. Diese Methode war einfach, kostengünstig und hochpräzise und kann eine Echtzeitüberwachung realisieren und gleichzeitig eine Forschungsgrundlage für einen stabilen Flug und eine präzise Steuerung von Flugzeugen für unbemannte Kampfplattformen bieten.