Oberflächenmorphologieanalyse eines triboelektrischen Nanogenerators auf Basis einer Strickstruktur zur Verbesserung der Transferladung

Einführung

Fortschrittliche Intelligenztechniken haben die globale Welt erobert und einige neuartige flexible intelligente tragbare Geräte wie Gesundheitsüberwachungssensoren [1, 2], Gestenerkennungsgeräte [3,4,5,6], elektronische Skins (E-Skins ) [7, 8], flexible Schaltungen [9, 10] und Glasfaser-Wearables [11, 12]. Mit den Nachteilen Massengewicht, geringer Wandlungswirkungsgrad, starker Umweltverschmutzung und kurzer Batterielebensdauer ist die Leistungsergänzung jedoch die enorme Einschränkung für die Entwicklung der Elektronik. Seit der erfolgreichen Entwicklung des ersten triboelektrischen Nanogenerators (TENG) im Jahr 2012 [13], basierend auf den Eigenschaften des kleinen Maßstabs, des geringen Gewichts, verschiedener Materialien, der Sicherheit, der Umwelteigenschaften [14] und der hohen Effizienz, bietet er einen vielversprechenden und effektiven Strategie zur Bewältigung der oben genannten Meerengen. Zusammen mit dem raschen Aufkommen von TENGs, die durch einen gekoppelten Effekt von Kontaktelektrisierung und elektrostatischer Induktion arbeiten [15], hat sich dies als ein wünschenswerter Ansatz erwiesen, um mechanische Energie [16, 17] aus unserer Umgebung zu gewinnen, insbesondere durch die Nutzung niederfrequenter und unregelmäßiger Bewegungen (einschließlich Wind [18, 19], Wassertropfen und menschliche Bewegung, biomechanische Energie usw. [20, 21, 22]), Realisierung von Datenübertragungen [23, 24, 25] und Energieergänzung im Internet der Dinge (IoT) [26]. Für tragbare Geräte gelten Textilien aufgrund ihrer Strukturbeständigkeit und Ermüdungsbeständigkeit, Weichheit, Integration und hohen Porosität als das beste Substrat. Bis heute ist die Integration eines triboelektrischen Nanogenerators und eines traditionellen Textils [27,28,29,30,31,32,33] einer der vielversprechenden Kandidaten für am Menschen orientierte tragbare Geräte wie batterielose flexible Sensoren [34] , tragbare Energy Harvester und textilbasierte Energiespeichersysteme. Es verleiht auch konventionellen Textilien Funktionalität, Intelligenz und einen hohen Mehrwert. Diese auf Textilien basierenden elektronischen Geräte erfüllen die Anforderungen an Leichtgewicht, Preiswert, Komfort, Atmungsaktivität, Tragbarkeit, Langlebigkeit und Waschbarkeit für den täglichen Gebrauch. Darüber hinaus ist es leicht, Textilien mit variablen Farben und üppigen Musterdesigns herzustellen, die für intelligente Textilien attraktiv sind. Insbesondere Stricktextilien mit geringer Dehnung und großer Verformung sind empfindlich gegenüber der Signalerzeugung und eignen sich daher ideal für flexible Sensoren, die Bewegungswiderstände überwinden und Energieverluste reduzieren [35]. Darüber hinaus sind Reibungen und Verformungen von gestrickten Textilien häufige Phänomene, die eine spannende Meinung für die Konstruktion eines triboelektrischen Nanogenerators sind.

Wie wir alle wissen, ist die Modifikation der Oberflächenmorphologie ein wichtiger Ansatz zur Verbesserung der Ausgabeleistung von TENGs [36,37,38,39]. Die meisten zielen darauf ab, die verfügbare Kontaktfläche und die Rauheit der Oberfläche zu erhöhen. Es gibt zwei Hauptverfahren, die die Oberflächenmorphologie ändern, eines ist das Oberflächenätzen und das andere die Oberflächenreplikation. Jedoch ist die Verwendung eines sehr teuren, begrenzten Behandlungsbereichs und einer mehrstufigen Herstellungstechnik zur Erzeugung eines Oberflächenaussehens für die industrielle Produktion schwierig. Hierin beschreiben Li et al. [40] untersuchten eine Polydimethylsiloxan(PDMS)-Folie mit vom Sandpapier abgeschälten Oberflächenmikrostrukturen, die eine Ein-Prozess- und kostengünstige Methode war, um die unterschiedliche Rauheit der Oberfläche vorzubereiten. Die experimentellen Ergebnisse zeigten die erzeugte maximale Leistung von 46,52 V unter der Rauheitsklasse von 3000, die durch ein optisches 3D-Oberflächenprofil nachgewiesen wurde. Außerdem können zu viele Mikrostrukturen die effektive Kontaktfläche stark verringern und zu einer Verringerung der Leistungsfähigkeit führen. Die Größe der TENGs war durch den Schleifpapierbereich begrenzt, was zu erhöhten Herstellungskosten führte. Heutzutage erhalten textile Strukturen aufgrund der Bildung reichlicher Oberflächenerscheinungen [38] ohne den komplexen Herstellungsprozess und die hohen Kosten zunehmende Aufmerksamkeit. Um das Erscheinungsbild von Textiloberflächen vollständig zu verstehen, müssen einige Faktoren in Bezug auf einzigartige Komponenten und Strukturmerkmale berücksichtigt werden, einschließlich der Fadenaussicht, der textilen physikalischen Parameter und der Strickstrukturen. Dann haben Kwak et al. [41] untersuchten die Kontaktfläche von drei Strukturen (einschließlich Glatt-, Doppel- und Rippgewebestrukturen) während der Dehnung und diskutierten den Beitrag zur Potenzialsteigerung. Es hat sich gelohnt, dass Rippengewebe bis zu 30% gedehnt werden kann und die Kontaktfläche auf 180 cm ² . vergrößert wird . Je nach vorhandenem Mittelbereich kann Rippengewebe stark gedehnt werden, wodurch ein höheres Potenzial zur Erhöhung der Kontaktfläche erzielt werden kann. Als primäres Element der textilen Struktur wurde die Charakteristik von Schlaufen analysiert, die auch maßgeblich die Oberflächenoptik beeinflusst. Huanget al. [42] konzentrierten sich auf die Wirkung grundlegender Textilparameter (einschließlich Schlaufenschenkel, Schlaufenplatinen und Stoffdichte), um den Unterschied auf die Ausgabeleistung zu bestätigen. Der triboelektrische Nanogenerator auf Stoffbasis mit großer Stichdichte könnte eine höhere elektrische Energie mit einer maximalen Spitzenleistungsdichte von 203 mW m ⁻² . erzeugen bei 80 MΩ, was eine größere effektive Kontaktfläche ergibt. Das Ergebnis zeigte, dass die Oberflächenmorphologien verschiedener Gewebestrukturen einen Einfluss auf die elektrische Leistungsfähigkeit hatten. Um viel mehr Energie für die Verlängerung der Lebensdauer zu gewinnen, wurden 3D-doppelseitige Interlock-Stich-Textilien [43] im Doppelnadelbett flach gestrickt, die auf Vorder- und Rückseite die gleiche Ausgangsleistung aufwiesen. Darüber hinaus könnten die auf der dreidimensionalen Textilstruktur basierenden TENGs eine hohe Leistungsdichte von 3,4 mW m ⁻² . erzeugen bei einem Außenwiderstand von 200 MΩ, was zeigt, dass die Kapazität des Energy Harvesting verbessert wurde. Die oben erwähnten Oberflächenerscheinungsformen geben jedoch wenig Aufschluss über die Geometrieform der Oberfläche, und Faktoren über die erzeugte Transferladung leiden noch an einem Mangel an spezifischen Erklärungen. Es gibt keine universelle Methode zur Charakterisierung der Oberflächenerscheinung, die eine Bewertung der unregelmäßigen Morphologie erfordert. Daher ist dies derzeit die Einschränkung für das vollständige Verständnis der Transferladung des triboelektrischen Nanogenerators.

Der Zweck der Oberflächenanalyse besteht darin, die geometrischen Strukturen von Textilien zu charakterisieren, die in zwei Ansätzen, der Kontaktmethode und der optischen Methode, getestet werden können [44]. Die Kontaktmethode kann die Oberflächenmorphologie gut beschreiben, aber die benötigte Zeit ist viel länger und die Nadel hinterlässt eine Spur auf der Oberfläche. Im Vergleich zur Kontaktmethode mit den Vorteilen der kurzen Messzeit, der geringen Kabelbaumoberfläche und der einfachen Erkennung wurde die optische Methode zur Erkennung der Oberflächenrauheit verwendet. Die falschen Lücken und der hohe Rauschpegel können jedoch die Beurteilung der tatsächlichen Oberflächenmorphologie beeinträchtigen.

Das mathematische Werkzeug ist eine Theorieanalyse, mit der das Ausmaß der Oberflächenrauheit quantifiziert werden kann. Es ist ein neuartiger Ansatz, um die unregelmäßige Oberfläche zu bewerten. Bei solch einer unebenen Oberfläche kann die herkömmliche mathematische Methode der euklidischen Geometrie nicht verwendet werden, da es wirklich schwierig ist, die quantitative Geometrieabmessung und Messgenauigkeit, wie Länge des Segments und Gewicht des Objekts, zu beurteilen. Es wurde jedoch die fraktale Geometrie, ein von Mandelbrot benannter Ansatz zur Beschreibung unregelmäßiger Strukturen, bereitgestellt, um das Problem zu lösen und die Unregelmäßigkeit in der Natur zu definieren [45], wie zum Beispiel die physikalischen Eigenschaften von Schäumen [46] und die Bewertung der Gewebeglätte [47] . Fast alle rauen Oberflächen können in einige selbstähnliche Teile unterteilt werden, die durch eine nicht ganzzahlige Dimension dargestellt werden können, die als fraktale Dimension bezeichnet wird (D _f ). Basierend auf den verschiedenen geometrischen Oberflächen ist der Wert von D _f berücksichtigt und analysiert werden muss, die sich auf die Rauheit und die effiziente Kontaktfläche beim Design eines triboelektrischen Nanogenerators auswirkt, wodurch die Fähigkeit zur Umwandlung menschlicher Bewegungen in elektrische optimiert wird.

Hier, in dieser Arbeit, präsentieren wir die verschiedenen Oberflächenmorphologien basierend auf Strickstrukturen, die als eine der dielektrischen Schichten verwendet werden. Das auf Stricktextilien basierende TENG wurde unter Verwendung kommerzieller Fäden und einer industriellen Strickmaschine hergestellt, die die Großserienproduktion und praktische Anwendungen realisieren kann. Um die flatternde Handbewegung zu imitieren, sind TENGs im kontaktgetrennten Arbeitsmodus (CS) ausgeführt, dem einfachsten Arbeitsmechanismus. Die Strickstrukturen werden auf zwei Arten gebildet, einschließlich der strukturierten und formbasierten konvex-konkaven Oberflächenmorphologie. Aufgrund der Vielfalt der Strickstrukturen können die resultierenden Oberflächenerscheinungen systematisch untersucht und analysiert werden, um den Zusammenhang zwischen Oberflächenmorphologie und Strickstrukturen zu bestätigen. Das D_f jedes Gewebes kann durch das entsprechende fraktale Prinzip berechnet werden, indem die Rauheit der Gewebeoberfläche bewertet wird. Die maximale Übertragungsladung des Oberflächenerscheinungsbildes in einer 1*1-Rippe kann bis zu 91,66 nC durch Flattern und Loslassen erreichen, wodurch die fraktale Dimension von 0,99 erreicht wird. Und ein interessantes Phänomen zeigt dies mit dem Wert von D _f schließend auf die Nummer eins kann die Übertragungsgebühr höher sein. Schließlich kann die Verwendung der Fraktaltheorie und der Strickstrukturen eine effektive Methode zur quantitativen Bewertung der Transferladung darstellen und soll helfen, die TENGs auf Stricktextilbasis mit mehr Effizienz, industrieller Produktion und kostengünstigeren Kosten zu entwickeln.

Materialien und Methoden

Materialien

Die handelsüblichen Nylongarne (dtex 600, AnTong KeJia Textile fiber products Co., Ltd.) wurden auf der gesamten Bekleidungsmaschine (SHIMA Seiki Co., Japan). Es wird ein Film aus Polytetrafluorethylen (PTFE) mit einer Dicke von 0,05 cm (Chenqi Electrical Technique Co. Ltd.) verwendet. Die gebogene und verdrillte Elektrode ist eine handelsübliche Kupferfolie (Shenzhen Biaozhitape Co. Ltd) mit einer Dicke von 0,06 mm, die auf die Rückseite des gestrickten Textils geklebt wird, um polarisierte Ladung zu übertragen.

Herstellung der Maschenware und des triboelektrischen Nanogenerators auf Strickstoffbasis

Die Schusstechnik als repräsentatives Strickverfahren kann Stoffen leicht eine hohe Dehnbarkeit [48], geringe Kosten und ästhetische Leistung verleihen. Mit den Vorteilen des Positionsstrickens lassen sich die Powertextilien ohne zusätzliche Nähtechniken in die Kleidung integrieren. Es gibt zehn entworfene konvex-konkave Texturen, die in Tabelle 1 dargestellt sind. Um die Beziehung zwischen Oberflächenmorphologie und Übertragungsladung zu demonstrieren, werden Längen- und Querkorde auf der Oberfläche des Textils gestrickt. So sind in Tabelle 1 zehn verschiedene Texturen dargestellt, wobei die ersten sieben Proben eine Längskordel auf der Oberfläche aufweisen und die Oberflächenerscheinungen von Nr. 8, nein. 9, und nein. 10 sind querkonvex. Hier werden die Strukturen von einer computergesteuerten Flachstrickmaschine, die für einen hocheffizienten industriellen Prozess geeignet ist, eingestrickt und die Textilien können auf den individuellen Maßstab zugeschnitten werden. Über das eigene Designsystem lassen sich Stoffe schnell gestalten und einfach vorbereiten, insbesondere für die Gestaltung filigraner Muster. Alle Stoffe müssen 24 Stunden lang unter den üblichen atmosphärischen Bedingungen zum Relaxieren von Stoffen in den maßstabilen Zustand belassen werden, die darauf abzielen, den Einfluss der Relaxationsschrumpfung zu verringern und das Ergebnis der Testgenauigkeit zu verbessern. Anschließend wurde die Rückseite der Textilien mit leitfähigem Klebeband der gleichen Größe beklebt. Basierend auf den hochpolarisierbaren Nanopartikeln wurde als weitere dielektrische Materialien die Folie aus PTFE übernommen. Der Film haftet noch an einem Stück Kupferfolie und überträgt die Elektronenwanderung. Beim CS wurden leitende Drähte mit zwei Reibungsmodellen verbunden, die sich in vertikaler Richtung bewegen. Dann wurden die CS-basierten textilen TENGs hergestellt.

Fraktale Zeichen von Strickstoffen

Nicht alle natürlichen Objekte haben eine unvollständige regelmäßige Form und Grenze, einschließlich Küstenlinie, Schneeflocke, Wolken und Blätter. Daher wird die fraktale Dimension verwendet, um die durch verschiedene Methoden erzeugte ungleichmäßige Morphologie zu beschreiben, was eine effektive Methode ist, die in vielen Forschungsarbeiten identifiziert wurde. Es gibt mehrere Formulierungen, die als fraktale Dimension definiert sind, einschließlich der Hausdorff-Dimension, der Zählbox-Dimension und ähnlichen Dimensionen et al., die der entscheidende Parameter zur Quantifizierung des Oberflächenstils sind. Die typische fraktale Dimension war die Kohn-Kurve wie eine Schneeflocke, die erstmals 1904 vorgestellt wurde. Der Bereich, der von drei Selbstähnlichkeiten mit unendlich begrenzt wird, wird als Kohn-Kurve bezeichnet, deren fraktale Dimension 1.2618 ist. Im Allgemeinen kann die fraktale Dimension anhand der Skala a berechnet werden, die Länge, Breite und Fläche angibt. Die folgende Formel kann die Beziehung darstellen:

wo D _f ist die fraktale Dimension, die sich in der Steigung eines Log-Log-Plots zeigt.

Die fraktale Dimension der unebenen Oberfläche, D _f , kann in einem Ansatz der Hausdorff-Dimension bestimmt werden, der auf der relativen Größenanalyse einer ähnlichen Einheit basiert. Als Faktor zur Bildung der Kordoberfläche kann der konvexe Bezirk, der mehrere mikrokonvexe Struktureinheiten mit unterschiedlichen Kanten und Anzahlen umfasst, ausgedrückt werden als:

wo M ist die Zahl der konvexen Einheit, N die wiederholten mehrfachen selbstähnlichen Einheiten sind, die die Länge der konvexen Einheiten zur Länge ganzer Samples sind, und D _f ist die fraktale Dimension der erhabenen Strukturen. Die Gleichung ist ein Modell, das verwendet werden kann, um die Oberflächenmorphologie vorherzusagen, also:

Charakterisierung

Das digitale Dino-lite Edge-Mikroskop (AnMo electronic Corporation) wurde verwendet, um die Dichte von Strickwaren aus Fotobildern zu messen. Die elektrischen Signale des triboelektrischen Nanogenerators aus gestricktem Gewebe im Kontaktierungs- und Trennmodus wurden von einem selbstaufbauenden Linermotor und einem Elektrometer (Keithley 6514-System) basierend auf dem LabVIEW-System betrieben.

Ergebnisse und Diskussion

Um Reibungsmaterialien zu bestätigen, ist die triboelektrische Ordnung [49] die maßgebliche Referenz, die die triboelektrische Polarisation verschiedener üblicher Materialien quantifiziert. Die triboelektrische Ordnung zeigt, dass eine Seite eine zunehmende Ladungskapazität zeigt und die andere Seite eine hohe Fähigkeit besitzt, Elektronen zu verlieren, die als grundlegende Materialleistung definiert wurden. Um die herausragende Ausgangsleistung zu erzielen, werden einige Materialien ausgewählt, die mit erheblichem Abstand der triboelektrischen Reihe zugeordnet werden müssen, was die Potenzialdifferenz erhöht. Hierin ist das eine die kommerzielle, kostengünstige, ausgezeichnete Abriebfestigkeit und stark positiv geladene Tendenz (Nylon) und das andere zeigt negativ geladene Tendenz (PTFE). In dieser Arbeit haben wir die PTFE-Membran ohne Behandlungen an der Oberfläche ausgewählt. Der einzige Faktor sind hier Strickstrukturen, die durch die Leistung der Ladungsübertragung analysiert werden können. Ein weiteres kritisches Element ist das Elektrodenmaterial, eine Kupferfolie mit hoher Flexibilität, die direkt aufgeklebt werden kann, dh ein einfacher und einstufiger Herstellungsprozess. Im Vergleich zu den Edelmetallen Silber und Gold ist der Preis für Kupferfolie günstig und kann zur Herstellung kostengünstiger Produkte verwendet werden. Kupfer wird daher häufig als flexible Schaltkreise und Elektroden beim Design intelligenter Geräte verwendet.

Gegenwärtig gibt es vier universelle, im Arbeitsmodus betriebene TENGs, die den unterschiedlichen Elektrodenstrukturen und -bewegungen entsprechen. Mit den Vorteilen der einfachen Herstellung, der reichhaltigen Materialauswahl und der hin- und hergehenden Bewegungen in vertikaler Richtung sind die CS TENGs die ersten eingehend untersuchten, die die potenzielle Fähigkeit haben, biomechanische Energie wie Schlagen mit den Händen, Gehen und Laufen zu gewinnen. Um hier das Einflussprinzip der Oberflächenstrukturen zu untersuchen, wurden die triboelektrischen Nanogeneratoren auf Basis von gestrickten Textilien (KNGs) konstruiert, die dem Kontakt und der Trennung zwischen Nylongewebe und PTFE-Folie entsprechen. Der Aufbau des triboelektrischen Nanogenerators ist in Abb. 1a dargestellt, bestehend aus Gewirke, PTFE-Membran und Kupferfolie. Die Vielseitigkeit flexibler Maschenware hinsichtlich ihrer Fähigkeit zum Kräuseln (Abb. 1 bi), Biegen (Abb. 1 bii), Drapieren (Abb. 1biii) und Falten (Abb. 1biv) in jede Richtung ist in verschiedenen Maßstäben zugeschnitten in Abb. 1b dargestellt. Die KNGs können je nach Anforderung der Anwendungsposition und der Ästhetik der Kleidung entworfen werden. Die Vielfalt der Strickstrukturen wurde mit unterschiedlichen Oberflächenoptiken gestrickt, und diese Fotografien der textilen Oberfläche wurden dann in Abb. 1c gezeigt.

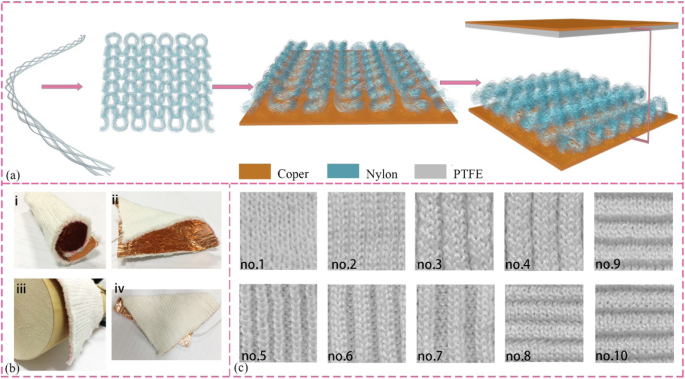
Schematische Darstellung, charakteristisch für KNG und Strickstruktur. a Herstellungsprozess von KNG. b Bilder von KNG unter verschiedenen Verformungen. ich, gekräuselt; ii, gebogen; iii, drapiert; iv, gefaltet. c Alle hergestellten Strickstrukturen, von Nummer 1 bis 10

Der Betriebsmechanismus der KNGs ist in Abb. 2a einfach dargestellt. Um die Übertragungsladung zu messen, werden der maximale Abstand und die Bewegungsfrequenz des Linearmotors auf 10 cm bzw. auf 0,3 Hz eingestellt, um die Bewegungen der flatternden Hände zu simulieren. Bei der üblichen Überwachung werden die Leerlaufspannung (Voc), der Kurzschlussstrom (Isc) und die Transferladung (Qsc) von einem mechanischen Linearmotor gemessen. Im Originalzustand (Abb. 2 ai) erzeugte das Nylontextil positive Ladungen und PTFE-Folie war aufgrund der elektrostatischen Induktion und Ladungserhaltung mit negativen Ladungen aufgeladen. Wenn das Gerät gedrückt wurde (Abb. 2 aii), führt eine Schrumpfung des Spalts zwischen den beiden Kontaktflächen dazu, dass sich die positive Ladung in der auf das PTFE geklebten Elektrode ansammelt. Die Elektronen fließen aus dem externen Stromkreis, um die Potentialdifferenz auszugleichen. Es war erwähnenswert, dass die äquivalente Menge an Elektronen auf der Oberfläche der Kontaktfläche gehalten werden kann, da beide dielektrischen Materialien Isolatoren sind (Abb. 2 aiii). Wenn sich das PTFE zurückbewegt (Abb. 2aiv), kehrt sich der Prozess um und das elektrische Gleichgewicht wird wieder zwischen Nylongewebe und PTFE hergestellt, was die Neutralisation der Ladungen widerspiegelt. Folglich fließen die Elektronen für elektrische Potentialunterschiede zurück. In dieser Situation könnten die KNGs Isc und Voc erzeugen, die eine charakteristische periodische Änderung aufweisen, wie in Abb. 2 b und c gezeigt. In Abb. 2b und c ist der Einschub ein vergrößerter Graph, der in einem Zyklus beschrieben wird.

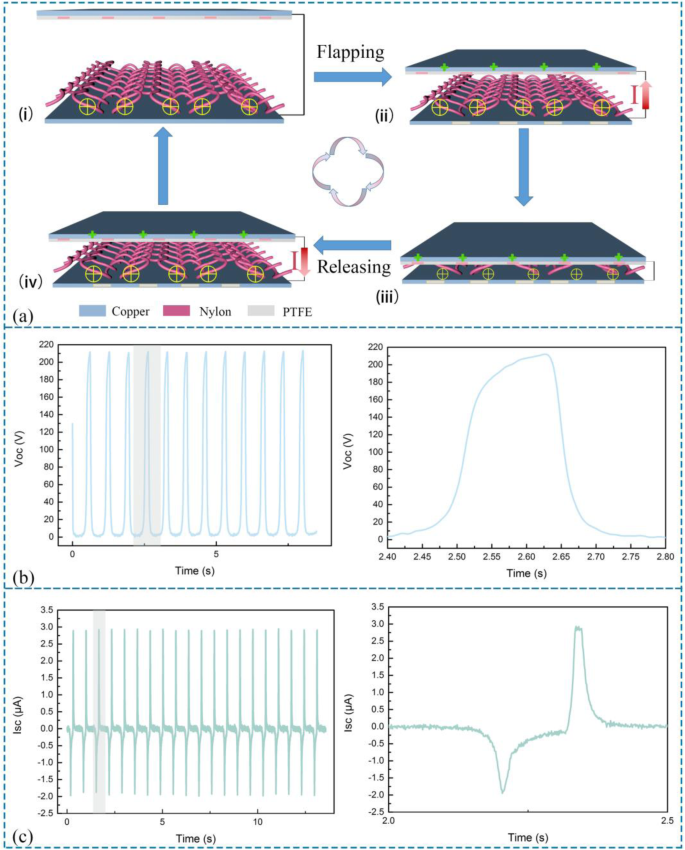
Elektrischer Arbeitsmechanismus und die Ausgangsleistung von KNG. a Betätigungsmechanismus von KNG unter Verwendung von Nylongewebekontakt mit PTFE-Element. b Voc von KNG und vergrößertes Bild für einen Zyklus. c Isc von KNG und vergrößertes Bild eines Zyklus

Um konvexe Strukturen auf der textilen Oberfläche herzustellen, gibt es zwei Arten von Methoden, einschließlich Strukturdesign und Formbildung, wie in Abb. 3 gezeigt Schleifenstiche. Die Gesamtstichproben sind in sieben Rippentypen ausgelegt, einschließlich des Typs m*n (m =n =1, 2, 3, 4) in Abb. 3a und 2*m (m =1, 2, 3, 4) in Abb. 3b gezeigt. Die Rippe hat eine vertikale Kordeloptik aufgrund der vorderen Maschenstäbchen, die dazu neigen, sich über und vor die umgekehrten Maschenstäbchen zu bewegen; dann kann die maximale Kabelhöhe 0,2 cm betragen. Die Rippe von m*n (m =n =1, 2, 3, 4) kann durch abwechselnde Maschenstäbchen von Gesichtsschlaufen auf jeder Seite ausgeglichen werden, so dass es nach dem Schneidern flach ohne Locken liegt. Und beide Seiten des Textils haben das gleiche Aussehen wie in Fig. 3e gezeigt. Durch die unterschiedlichen Proportionen von Stirn- und Rückschlaufen bei 2*m Rippenstrukturen kommt jedoch eine Unterscheidungsfläche zum Vorschein, wie in Abb. 3f dargestellt. Darüber hinaus wird der Streckprozess von Rippenware in zwei Stufen unterteilt, wobei die Rückstäbchen auf beiden Seiten ineinander greifen, bis sie gedehnt werden, um die Rückmaschenstäbchen dazwischen freizugeben, und dann werden ganze Schlingen weiter über die doppelte Breite des Äquivalents gedehnt einzelner Stoff. Daher haben Rippentextilien im Vergleich zu glatten Stoffen das Potenzial, die Dehnbarkeit für das Ernten von Schlag- und Streckbewegungen (Querrichtung und Längs) während des Kontakttrenn-Arbeitsmodus zu erhöhen. Das andere Verfahren zum Herstellen einer erhabenen Struktur ist die Formverformung, bei der die Luftschicht auf der Oberfläche des n . gebildet wird (n =4, 5, 6) Textil, das in Abb. 3c dargestellt ist. Die Dicke der Querschnittsfläche liegt im Bereich von 0,15 bis 0,3 cm. Charakteristisch für die Luftschicht ist eine markante Bogenstruktur, die beim Auslösen von Bewegungen etwas Raum für die Beschleunigung der Elektronentrennung bieten kann. Vor allem werden gestrickte Textilien durch eine computergesteuerte Flachmaschine entworfen, die die Genauigkeit der Strickposition realisieren kann, das gesamte Kleidungsstück formt und intelligente Materialien perfekt in den Stoff integriert. Eine solche Stricktechnik-Nomenklatur ist in Abb. 3d markiert, die die Strukturmerkmale korrekt wiedergibt.

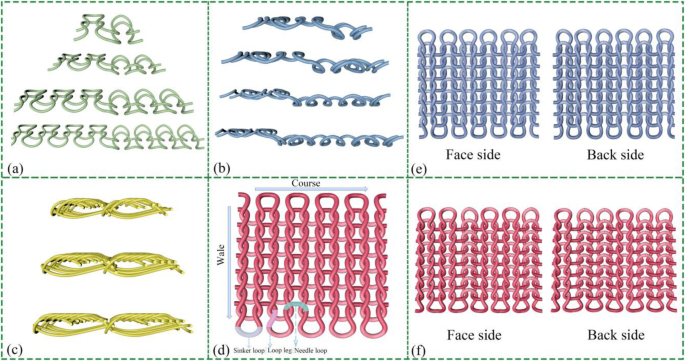
Schematische Eigenschaften und Komponenten von Strickstrukturen. a Eigenschaften der m*n-Rippe. b Eigenschaften der 2*m Rippe. c Eigenschaften einiger horizontaler Nadelschnur. d Nomenklatur der Stricktechnik. e Abbildung der Vorder- und Rückseite in der 1*1-Rippenstruktur. f Abbildung der Vorder- und Rückseite in 2* 1 Rippenstruktur

Frühere Arbeiten [42] zeigten die effektive Kontaktfläche der Vorderseite, die viel größer war als die der Textilrückseite; Ergebnis der Übertragungsladung war doppelt so hoch wie die Ausgabeleistung der Rückseite. Dies liegt daran, dass die Länge der Nadelschlaufe länger war als die der Platinenschlaufe. Um die Abtriebsleistung zu steigern und nur einen Einflussfaktor zu schaffen, bestehen die kontakterhabenen Strukturen daher aus stirnseitigen Schlaufen. Die Leistungen der KNGs in Abhängigkeit von der Anzahl der konvexen Einheiten sind in Abb. 4 aufgetragen. Es bildete sich ein abnehmender Trend, bei dem die Kontaktfläche aller untersuchten Textilien mit der Anzahl der erhabenen Einheiten abnahm. Außerdem liegen die signifikanteren elektrischen Ladungen in der sequentiellen Reihenfolge der 1*1-Rippen-, 2*1-Rippen- und vier nadelförmigen Strukturen (der erste Punkt jeder Linie) mit den Werten von 91,66 nC, 90,19 nC und 69,64 nC bzw..

Die Ausgabeleistung ändert sich durch die Anzahl der konvexen Einheiten

Anschließend wird die Strickstruktur mit der unterschiedlichen Oberflächenmorphologie in Bezug auf die Vielfalt der Maschenstäbchendichte, Anzahl der Vorderseiteneinheiten und Strukturen untersucht. Alle Parameter von zehn Arten gestrickter Textilien werden getestet und in Tabelle 2 aufgezeichnet. Bemerkenswert ist, dass die Maschendichte immer konstant ist, da das Kordaussehen bei der Analyse der Proben Nr. 1–7 in vertikaler Richtung gewachsen ist. Die Maschenstäbchendichte als Hauptfaktor, der diskutiert werden muss, bezieht sich also auf die Eigenschaften verschiedener Strickstrukturen. Es ist offensichtlich, dass bei den Nrn. 1-4 die Gesichtsschleife und die Rückwärtsschleife den gleichen Anteil haben, etwa 50%. Diese Textilien zeigen auf Basis des Doppelmaschenstricks auf der Vorder- oder Rückseite die gleichen Strukturen. Die durchschnittliche Dicke ist im Vergleich zu den Musternr. 5–7, die aus einer unterschiedlichen Anzahl von Gesichtsstichen und Reservestichen besteht. Textur-Nr. 4 besitzt die größte Wiederholungseinheit, bei der die Maschenstäbchendichte doppelt so groß ist wie die von Nr. 1. Allerdings ist die Anzahl der Vorderseiteneinheiten auf dem praktischen Stoff fast um die Hälfte geringer als bei Nein. 1. Dies liegt daran, dass mehr Platinenschlaufen miteinander gedehnt werden, damit das Säulenbild gebildet werden kann. Mit zunehmender gestrickter Einheit werden der Durchmesser der Säule und die Dicke der Stoffe vergrößert, wodurch die Anzahl der stirnseitigen Einheiten und die effiziente Kontaktfläche beim Auslösen von Bewegungen verringert werden. Hinsichtlich der Rippenstruktur mit unterschiedlichen Anteilen von Vorder- und Gegenmasche weist das Erscheinungsbild deutlich die Charakteristik einer einseitigen Struktur auf, wobei die gestrickten Rapporteinheiten zunehmen. Inzwischen ist die Waldichte von Nr. 7 ist so groß wie Nr. 1 und Nr. 5, aber die Anzahl der Gesichtsschlaufeneinheiten weist aufgrund der Anzahl der gestrickten Einheit deutliche Unterschiede auf, beträgt sechs Schlaufen, die viel mehr sind als keine. 1 (2 Schleifen) und Nr. 5 (3 Schleifen), so dass die Ausgangsleistung geringer ist als die von Nr. 1 und Nr. 5. Als Ergebnis wird die Rippenstrickware Nr. 1 steht für die meisten Face-Loop-Einheiten in Nr. 1–10 während der Kontaktierungs-Trennungsbewegungen.

Auf der anderen Seite wurde das formgestrickte Textil durch die unterschiedliche Anzahl von Schlingen entworfen, die sich zu dem gesamten Gewebe zusammenfügen und Bogenstrukturen bilden. Da die Kordlängenrichtung horizontal ist, zeigt die Maschenstäbchendichte des Gewebes eine ungefähre Stabilität in Querrichtung. Die Bogenstruktur bietet einen Ansatz zur Ladungstrennung an der Oberfläche, die einen hohlen Innenraum aufweist. Somit wurde die Effizienz der Gewinnung von Energie des verschwendeten Mechanismus verbessert. Um die Ausgabeleistung zu verbessern, wird ein Bogentyp im Allgemeinen aus flexiblen Materialien mit perfekter Elastizität und Haltbarkeit hergestellt, wie beispielsweise Silikonsubstraten, aber es ist schwierig, in industriellen Strickmaschinen gestrickt zu werden, um die kommerziellen Anforderungen zu erfüllen. Wenn in früheren Untersuchungen [24, 41, 50] die Gewölbestruktur dem gestrickten Textil nachempfunden ist, muss die Konstruktion aufwendig und zeitaufwendig vernäht oder verklebt werden. Wir präsentierten ein gestricktes Bogengewebe, das durch die gesamte Umformtechnik ohne zweite Herstellung hergestellt wird und die hohe Effizienz der Produktion ermöglicht. Unter den horizontalen Kordstrukturen weist die 0,3-cm-Höhe die geringste Ladungsabgabe im Vergleich zu der vier- und fünfnadeligen horizontalen Kordstruktur mit einer Höhe von 0,15 cm bzw. 0,2 cm auf, die durch die geringe Steifigkeit von gestrickten Textilien beeinflusst werden kann ein großer Abstand zwischen beiden Enden fest. Die höchste konvexe Form ist mit Kraftdruck schwer zu halten und wieder in die ursprüngliche Form zu bringen, was dazu führt, dass einige Ladungen neutralisiert werden. Als Ergebnis kann die Verringerung der Bogenhöhe die Toleranz von konvexen Strukturen verbessern. Jedoch verringern solche Formkabel die effektive Kontaktfläche, die ein Leitungstyp ist, der wenig Flächen als der tatsächliche Kontakt hat, wodurch die Leistung der elektrischen Ausgabe verringert wird.

Schlingen haben unregelmäßige Strukturen, daher ist die Bewertung ihrer Geometrieeigenschaften wie Stichgröße und Oberflächenform eine Herausforderung. Um die Unregelmäßigkeit der Schleifen zu erkennen, kann die traditionelle Bewertung, die eine integrale Dimension darstellt, nicht verwendet werden. Die Fraktaltheorie wird vorgeschlagen, um die Kategorie der Unregelmäßigkeit in unserer Umgebung und Natur zu analysieren. Das vorgeschlagene Konzept der fraktalen Dimension ist ein ausgezeichnetes Werkzeug, um komplexe Morphologien darzustellen, die die Regeln, die Komplexität und die Rauheit der textilen Oberfläche darstellen. Da nicht alle Fraktale vollständig selbstähnlich sind, wird die mathematische Berechnung verwendet, um die Geometriekonfiguration zu argumentieren. Um die Oberfläche der Strickstruktur zu verstehen, visualisieren einige Bilder die in Abb. 5d enthaltenen Informationen. Wie in Abb. 5d gezeigt, kann die Charakteristik der konvexen Oberfläche intuitiv aus verschiedenen Perspektiven beobachtet werden, wobei der Beweis für die Bestätigung der erhabenen Morphologie ist.

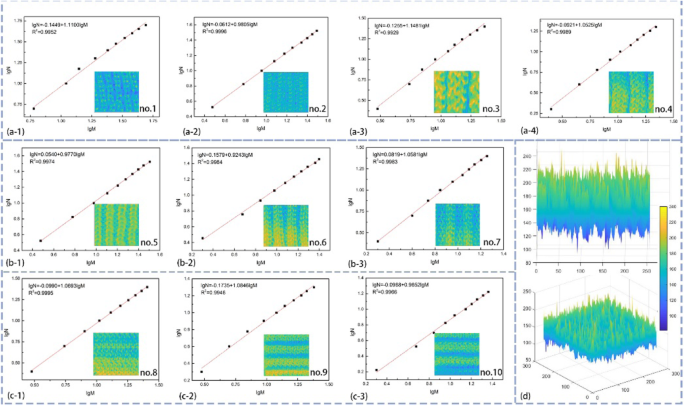
Passformkurve und einige visuelle Bilder zum Stricken von Textilien. a Die m*n-Rippenstruktur. b Die 2*m Rippenstruktur. c Some needle horizontal cord structure. d The visual images from different aspects

The uneven surface has been formed with the knit structure designed caused by the yarn morphology and structure design. The fractal geometry is an efficient calculation for evaluating the textile surface and understanding the characteristic of knitted structures and ability of triboelectric charge generation. In fact, with the increase of the raised unit, it can improve the uneven knitted textile owing to the surface shape modified. Although all of the knitted textile own convex structures in longitude and transverse direction, the degree of similarity is still not confirmed that is the significant reference value for whether using fractal dimension successfully or not. To estimate the feasibility of fractal dimension, all of the knitted fabrics are calculated through measuring the width of the convex unit, the size of loops in length, and width when textiles stay in stable size. Figure 5 a, b, and c show the fitting curve of fractal dimension of nos. 1–10 type fabrics, and slope of a line means the fractal dimension. The existence of the relationship is found in convex structures of the ten different types of knitted textiles, which confirms the fractal characteristic of ten knitted fabrics. Therefore, the fractal theory applied in the analysis of diversity knit structure that is practicable.

Figure 6a–f illustrates the generated Isc and Voc based on the practical applications of contact and separation working KNGs, based on the structure types and shape types. There is a trend that a decrease with the knit unit increases about the Isc and Voc as shown in Fig. 6a–f. This is because the Isc is changed with the effective contact area which is affected by knit structures.

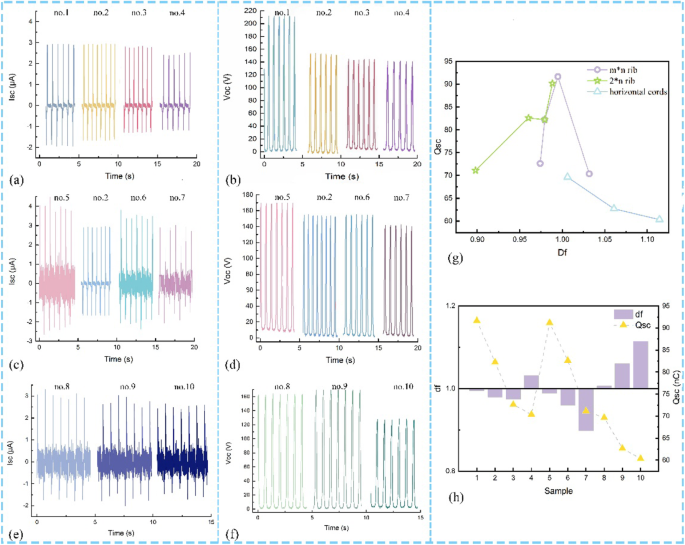
Schematic illustration of fractal dimension and generated Isc and Voc. a The Isc of m*n rib. b the Voc of the m*n rib. c The Isc of 2*m rib. d The Voc of the 2*m rib. e The Isc of n type. f The Voc of n type. g The D_f -transfer charge curve. h The F value curve

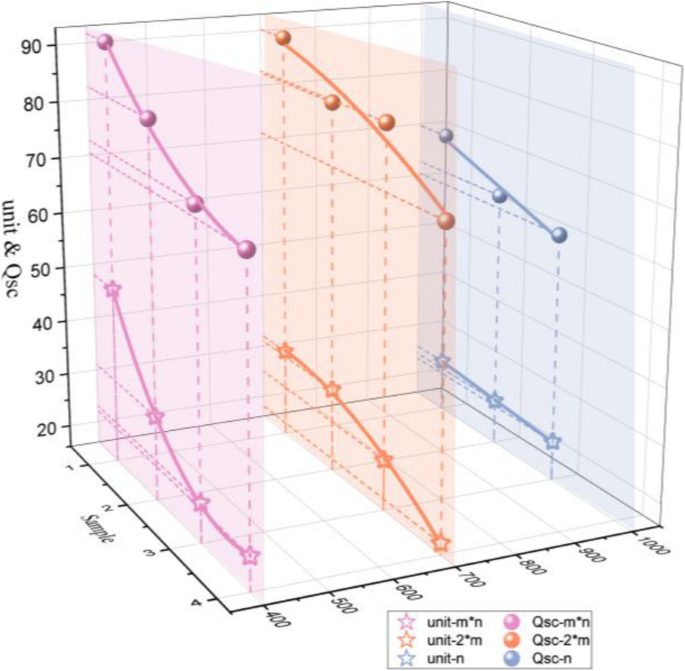
When calculating the D _f of various knit structures, the investigated knit structure states that the different knit structures have an unequal value which is non-integral dimension due to the different components of convex as demonstrated in Fig. 6g. As for Fig. 6g, this is the image of the transfer charge versus fractal dimension curve of diversity structures. The rib structure presents desirable output performance and the fractal dimension near the value of one. The TENGs based on structure-type knitted-textiles have a higher transfer charge than shape type and the value of D _f about the m*n rib type, 2*n rib type, and n type is in the range of 0–2, 0–1, and 1–2, respectively. Generally, the fractal dimension symbolizes the extent of surface roughness which is the roughness increasing with the large D _f . However, the shape-type fabrics are designed in horizontal cord with small line-contact area, so the roughness has little influence on the transfer charge.

In order to demonstrate the influence on D _f of convex structure homogeneity in rib structures, the random side length is chosen and calculated. The result exhibits as follow:

where a is the length of the whole fabric, b is the width of the convex unit and is equal to the width of the whole fabric, l is the length of the convex unit, M is the number of the convex unit, N is the repeated multiple of self-similar units that is the length of convex units to the length of whole samples, and ε is the proportion of face loop and reverse loop, meaning the uniform of the convex distraction.

Then, the calculation of M and N can be used in the formulation (1-3), the result shows that obtained D _f is not the same with the D _f that is calculated based on the length of actualmeasurement as shown in Table 3. No matter how the raised structure is distributed, the value of D _f is affected by the practical length and number of cords.

It is noted that the fractal dimension of the 2*1 rib structure is close to the 1*1 rib reach at 0.99, and thus, the transfer charge is much the same as shown in Fig. 6g. The generated electrical-output performance shows the highest when the D _f is near the value of one. That has provided one guess if the fractal dimension can evaluate the surface morphology and character the output performance. To investigate the correlation of fractal and transfer charge, the difference between the fractal dimension and the value of one (named F value) has been illustrated in Fig. 6h. The operating results show a trend that is decreased F value can boost the much higher Voc, taking evidence for potential application of fractal dimension. However, the F value is regarded as an evaluation of the roughness structures, which needs to consider the properties of the primary loop of the structure. Then, the influence on transfer charge is discussed comprehensively. The sample of no. 4 and no. 6 has a similar F value, but the massive difference exists on both of output performance. The surface morphology of no. 4 shows the planar structure due to the same number of face and reverse loops, so the transfer charge is low. But no. 6 has prominent appearance due to the reverse loops over the face stitches and the generated large transfer charge when contacting and separating. Therefore, the selection and design of the knitted structure of the textile based on the F value highly improved the generated total electrical charge, which is an indispensable requirement for construct a high-effective flexible self-power device based on the knitted textiles.

Conclusion

We have demonstrated that the knitted textile with high flexibility and excellent transfer charge can be applied in flexible TENGs for harvesting irregular and low-frequency biomechanical energy, which owns an outstanding output performance. To identify the relationship between surface morphology and output property, fractal theory has been used to quantify the surface geometry and used to evaluate its influence on the transfer charge ability of surface appearance. Different knit structures have been fabricated that can analyze their impact on energy harvesting. From the aspect of the knitted unit, the result shows that the maximum output of 1*1 rib structure can reach at 213 V with the minimum knitted unit. In addition, to further understand the working mechanism and the geometry of contact area, the various knit structures have been illustrated in a fractal dimension that is distinct from traditional dimension. Through calculation, different knitted structures with identical knit units can be used to obtain fractal dimension with the same knit units. The generated electrical output can be increased with the fractal dimension close to the value of one. Therefore, the difference between the fractal dimension and the value one can be used in the evaluation of transfer charge ability according to the irregular surface. In the near future, it is expected that an evaluation for generating output ability based on fractal theory in constructing a triboelectric nanogenerator, obtaining maximum output performance to optimize the flexible self-power system for harvesting wasted human motions in our daily life will be investigated.

Verfügbarkeit von Daten und Materialien

All data generated or analyzed during this study are included in this published article.

Abkürzungen

E-skins:

Electronic skins

IoT:

Internet of Things

PDMS:

Polydimethylsiloxan

TENG:

Triboelektrischer Nanogenerator

PTFE:

Polytetrafluoroethylene

D_f :

Fractal dimension

CS:

Contact-separate working mode

KNG:

The triboelectric nanogenerator based on knitted textile

Voc:

The open-circuit voltage

Isc:

Short-circuit current

Qsc:

Transfer charge

F value:

The difference between the fractal dimension and the value of one