Analytisches Modell für die maximale Kanaltemperatur in Ga2O3-MOSFETs

Hintergrund

Galliumoxid (Ga₂ O₃ )-basierte Metall-Oxid-Halbleiter-Feldeffekttransistoren (MOSFETs) sind ausgezeichnete Kandidaten für die Leistungselektronik der nächsten Generation, die von zwei großen Vorteilen von Ga₂ . profitiert O₃ :die signifikant hohe Bandlücke (~ 4,8 eV) und qualitativ hochwertige Bulk-Kristalle, die zu geringen Kosten hergestellt werden [1]. Es wurden enorme Anstrengungen unternommen, um seine elektrischen Eigenschaften in allen Aspekten wie Stromdichte [2], Durchbruchspannung [3] und Leistungskennzahl [4] zu verbessern. Mit der experimentellen Bestätigung seines beispiellosen Potenzials für leistungselektronische Geräte [5,6,7,8,9] ist es nun von größter Bedeutung, die Leistung und Zuverlässigkeit von Ga₂ . zu untersuchen O₃ MOSFETs, wie das Thema Selbsterwärmungseffekte und damit die maximale Kanaltemperatur (T _max ), aufgrund seiner relativ geringen Wärmeleitfähigkeit (κ , 0,11–0,27 Wcm ⁻¹ K ⁻¹ bei Raumtemperatur) [1].

In den letzten Jahren wurden verschiedene Methoden zur Schätzung des T _max von Ga₂ O₃ MOSFETs wurden theoretisch und experimentell vorgeschlagen [10,11,12,13]. Im Allgemeinen können numerische Simulationen T . quantitativ abschätzen _max eines bestimmten Gerätes. Dies ist jedoch zeitaufwendig [14]. Andererseits ist die Extraktion von T _max durch Experimente wird immer unterschätzt [15]. Daher muss ein analytisches Modell erstellt werden, um das T . adäquat zu modellieren _max in Ga₂ O₃ MOSFETs, die eine ausreichende Genauigkeit mit Zeiteffizienz und qualitativen Bewertungen bieten können [14].

In diesem Papier schlagen wir ein analytisches Modell von T . vor _max für Ga₂ O₃ MOSFETs durch Anwendung der Kirchhoff-Transformation unter Berücksichtigung der Abhängigkeit von κ zur Temperatur und kristallographischen Richtungen für Ga₂ O₃ . Das vorgeschlagene Modell kann auf Ga₂ . angewendet werden O₃ MOSFETs mit nativen oder hochwärmeleitenden Substraten. Die Validität und Genauigkeit des analytischen Modells wird methodisch durch den Vergleich mit den numerischen Simulationen über COMSOL Multiphysics überprüft.

Methoden und Modellentwicklung

Das analytische Modell für T _max in Ga₂ O₃ MOSFETs werden basierend auf der in Abb. 1 gezeigten Struktur vorgeschlagen. Die wichtigsten Parameter der Struktur sind in Tabelle 1 aufgeführt. Tatsächlich wurde gezeigt, dass sich die Joulesche Erwärmung an der Drain-Kante des Gates in Ga_{2 O3 MOSFETs [13]. Um das Modell zu vereinfachen, wird angenommen, dass die Heizwirkung des Gates gleichmäßig ist [12] und aufgrund seiner vernachlässigbaren Dicke das Gateoxid vollständig durchdringen kann. Verschiedene Substratmaterialien unter Ga2 O3 Kanäle werden in diesem Modell berücksichtigt, z. B. Bulk-Ga2 O3 und hohe κ Materialien, die auf die Machbarkeit und Kompatibilität der Platine abzielen. Somit wird die Vorrichtung als ein zweischichtiges Problem angesehen. Das Substrat kontaktiert einen idealen Kühlkörper, sodass die Unterseite isotherm ist und seine Temperatur der Umgebungstemperatur entspricht (T amb , 300 K standardmäßig). An anderen Oberflächen des Bauwerks wurden adiabatische Randbedingungen auferlegt. Diese Randbedingungen lassen sich zusammenfassen als [14, 16]}

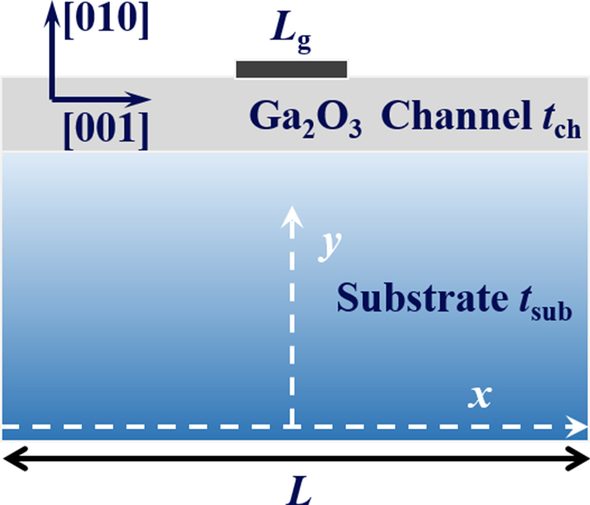
Das schematische Diagramm von Ga₂ O₃ MOSFET

wo P , T und κ _y bezeichnen die Verlustleistungsdichte, Temperatur und Wärmeleitfähigkeit der [010]-Richtung für Ga₂ O₃ , bzw. Es sollte betont werden, dass die Einheit von P ist in diesem Papier W/mm.

Die κ Wert von Ga₂ O₃ , einer der Schlüsselparameter für die thermische Materialeigenschaft, spielt eine wichtige Rolle bei der Diffusion der Wärmewirkung sowie der Genauigkeit des Modells. Das heißt, eine sorgfältige Beschreibung von κ Wert ist aufgrund seiner starken Anisotropie und Temperaturabhängigkeit erforderlich [17]. Im Allgemeinen ist die Abhängigkeit von κ von Ga₂ O₃ auf Temperatur (T ) entlang zweier unterschiedlicher Kristallorientierungen ([001] und [010]) ist gegeben durch

Die Vergleichsstudie von T _max an verschiedenen P wurde von COMSOL Multiphysics unter Berücksichtigung konstanter und realistischer κ . durchgeführt , bzw. Wir haben festgestellt, dass bei einem P von 1 W/mm, T _max Werte von 533 K bzw. 622 K werden erhalten (nicht gezeigt). Daher ist es unbedingt erforderlich, die Auswirkungen von T . zu berücksichtigen und kristallographische Richtung auf dem κ von Ga₂ O₃ im Modell.

Das Temperaturverhalten wird durch die Wärmeleitungsgleichung bestimmt. Die Wärmeleitungsgleichung im stationären Zustand in Ga₂ O₃ Domain ist

wo κ _x bezeichnet die Wärmeleitfähigkeit der [001]-Richtung für Ga₂ O₃ . Die nichtlineare Wärmeleitungsgleichung kann mit der Kirchhoff-Transformation gelöst werden. Die Anwendung der Kirchhoff-Transformation kann jedoch aufgrund der stark anisotropen κ in Ga₂ O₃ , die streng genommen nur für Materialien mit isotropem κ . gilt [14]. Angesichts der obigen Einschränkung sollte κ . nicht berücksichtigt werden _x und κ _y zwei unabhängige Variablen sein. Abbildung 2 zeigt die Beziehung zwischen dem thermischen Widerstand, d. h. 1/κ , und T für Richtungen von [001] und [010] über ein großes T Reichweite bzw. Es ist ersichtlich, dass 1/κ _y kann durch 1/(cκ . ersetzt werden _x ) und c gleich 1,64 gewählt wird. Folglich ist Gl. (6) lässt sich in die folgende Gleichung umwandeln:

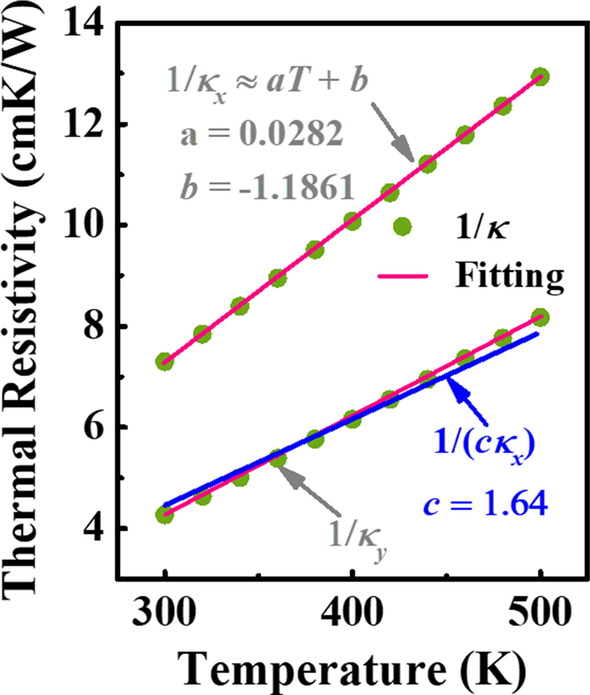
Die Beziehung zwischen dem thermischen Widerstand und T für Richtungen von [001] und [010]. Grüne Symbole und rote Linien kennzeichnen tatsächliche bzw. angepasste Werte. Die blaue Linie repräsentiert die Hypothese von 1/κ _y 1/(cκ _x ), wobei c = 1.64

Basierend auf den vorhergehenden Näherungen von κ _x und κ _y , ist die Kirchhoffsche Transformation uneingeschränkt anwendbar. Außerdem ist auch ersichtlich, dass der Kehrwert von κ wird erwartet, dass es proportional zu T ist Um die Rechenkomplexität zu reduzieren, wird der Ausdruck von 1/κ _x kann vereinfacht werden als 1/κ _x = aT + b , wie in Abb. 2 gezeigt. Der Grund für die Verwendung von a , b und c ist nur die Bequemlichkeit, die folgenden Gleichungen zu schreiben.

Durch die Anwendung der Kirchhoff-Transformation und der Methode der Variablentrennung wird der Ausdruck von T _max kann abgeleitet werden als

wo

Es sei darauf hingewiesen, dass S ist eine konvergente unendliche Reihe und ihr Näherungswert, der leicht zu erhalten ist, wird bei der Berechnung anstelle ihres tatsächlichen Wertes verwendet.

Im Fall von Ga₂ O₃ MOSFETs mit hohem κ Substrate kann die Kirchhoffsche Transformation theoretisch nicht direkt angewendet werden. Damit die Transformation gültig ist, müssen die Randbedingungen entweder isotherm sein (konstante T Oberfläche) oder haben eine feste Wärmestromdichte. Aufgrund der unterschiedlichen κ von Ga₂ O₃ und Substratmaterial werden diese beiden Randbedingungen am Ga₂ . nicht vollständig erfüllt O₃ /Substrat-Schnittstelle. In Anbetracht dessen, dass die κ von Ga₂ O₃ ist viel niedriger als hoch κ Substrat, eine Hypothese, die isotherme Grenzfläche zwischen dem Ga₂ O₃ und das Substrat, eingeführt wird. Diese Hypothese ist entscheidend für die Ableitung des Ausdrucks T _max und seine Gültigkeit wird später überprüft. In diesem Fall ist der Wärmewiderstand (R _TH ) von hohem κ Substrat, ein Verhältnis der Differenz zwischen den T _int und T _amb und das PW , d. h. R _TH = (T _int —T _amb ) / (PW ), kann berechnet werden als R _TH = LW /(κt _sub ), wobei W ist die Breite des Substrats [19]. Somit ist der Ausdruck der Temperatur von Ga₂ O₃ /Substrat-Schnittstelle (T _int ) ist

wo κ _sub ist die Wärmeleitfähigkeit des heterogenen Substrats, die als konstant angenommen wird. Außerdem sollte darauf hingewiesen werden, dass der thermische Grenzwiderstand zwischen Ga₂ O₃ und heterogene Substrate sind nicht im Modell enthalten. Daher wird mit Hilfe von Gl. (8), der Ausdruck von T _max für Ga₂ O₃ MOSFETs mit heterogenem Substrat können abgeleitet werden als

wo

Ergebnisse und Diskussion

Die Gültigkeit des analytischen Modells für das T _max in Ga₂ O₃ In diesem Abschnitt wurden MOSFETs systematisch verifiziert, wobei sowohl natives Substrat als auch das Gegenstück mit höherer Wärmeleitfähigkeit berücksichtigt wurden. Die Gültigkeit eines Modells lässt sich am besten anhand experimenteller Daten testen. Einige wichtige geometrische Parameter konnten jedoch in experimenteller Literatur nicht gefunden werden, wie zum Beispiel t _sub und L in Ref.-Nr. [12]. Daher wird die Finite-Elemente-Simulation, eines der genauesten Mittel, verwendet, um unser Modell zu verifizieren. Abbildung 3 zeigt die Abhängigkeit von T _max zur Leistungsdichte P erhalten aus COMSOL Multiphysics und analytischem Modell für Ga₂ O₃ MOSFET mit nativem Substrat. Es werden verschiedene Schlüsselparameter berücksichtigt, einschließlich der Gerätelänge L , Substratdicke t _sub , und Umgebungstemperatur T _amb . Wie in Abb. 3a gezeigt, ist das T _max wird natürlich mit der erhöhten Leistungsdichte erhöht und die Steigerungsrate wird mit dem kleineren L . verstärkt . Dies wird darauf zurückgeführt, dass das Gerät mit größerem L ermöglicht die Wärmeableitung aus dem aktiven Bereich und daher ist seine Gesamttemperatur niedriger als bei einem kleineren L gleichzeitig P [11]. Das heißt, es ist R _TH , die Steigung der Kurven, ist kleiner als die der letzteren. Da die κ . außerdem von Ga₂ O₃ sinkt mit steigender Gesamttemperatur, sein R _TH steigt auch langsamer als bei kleinerem L folglich, was in Abb. 3a [19] offensichtlich ist. Auch die Untersuchung der Abhängigkeit von T _max auf t _sub durchgeführt wurde, wie in Abb. 3b dargestellt. Es wird beobachtet, dass der Trend von T _max in Bezug auf P ist derselbe wie in Abb. 3a. Das dünnere Substrat erzeugt immer den abgeschwächten Anstieg von T _max über die vergrößerte Leistungsdichte, die verständlich ist, dass je dünner das Substrat, je niedriger die Gesamttemperatur, desto kleiner R _TH und seine Steigerungsrate, genau wie die Analyse in Abb. 3a. Abbildung 3c vergleicht den Einfluss von T _amb am T _max als P steigt. Es ist offensichtlich, dass die Differenz zwischen zwei Kurven langsam zunimmt, was sich von denen in Abb. 3a, b unterscheidet. Normalerweise R _TH wird von den geometrischen Parametern des Geräts und dem κ . dominiert Wert des Materials. Bedenkt man jedoch, dass die Struktur in diesem Fall feststeht, ist der Anstieg von R _TH wird nur durch die Abnahme von κ . induziert von Ga₂ O₃ . Andererseits wird ein hohes Maß an Übereinstimmung für das vorgeschlagene Modell beobachtet, das die T . berücksichtigt - und richtungsabhängige Beziehung für das κ von Ga₂ O₃ , was die skalierbare Natur des Modells bestätigt. Im Durchschnitt beträgt der Unterschied zwischen vorgeschlagenem Modell und Simulation  < 1 K. Die insgesamt beobachtete hervorragende Übereinstimmung deutet darauf hin, dass das vorgeschlagene Modell sehr effektiv und genau ist.

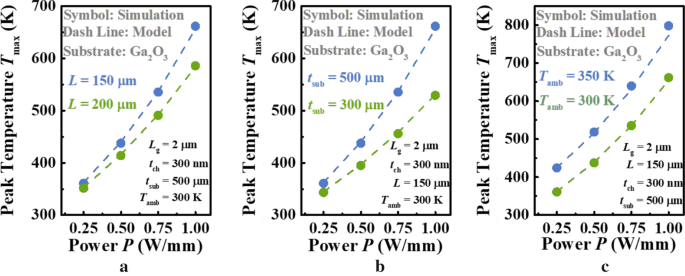
Abhängigkeit von T _max auf a die Länge des Geräts L , b die Dicke der Substratschicht t _sub , und c Umgebungstemperatur T _amb bei unterschiedlicher Leistung P . Symbole und Linien kennzeichnen die Ergebnisse des vorgeschlagenen Modells bzw. der Simulation

Ebenso werden, wie in Fig. 4 gezeigt, ähnliche Vergleiche für Ga₂ . wiederholt O₃ MOSFETs auf hohem κ Substrat, SiC. Hier die Schritte für L und T _amb die wir gewählt haben, sind größer als die in Abb. 3, und die unterschiedliche Kanaldicke t _ch wird anstelle von t . betrachtet _sub in diesem Fall. Andernfalls ist die Differenz zwischen zwei Kurven von T _max in Bezug auf P in jeder Figur ist aufgrund der effizienten Wärmeableitungskapazität des SiC-Substrats nicht zu unterscheiden. Die κ von SiC (3,7 Wcm ⁻¹ K ⁻¹ ) angewendet ist ein Standardparameter in der COMSOL Multiphysics Software. Dank hoher κ von SiC ist aus allen Zahlen deutlich zu erkennen, dass der Anstieg von T _max ist ungefähr linear als P steigt, was bedeutet, dass der Einfluss der Temperatur auf den R _TH des Gerätes ist vernachlässigbar. Es sei darauf hingewiesen, dass unser Modell diesen linearen Zusammenhang erfolgreich beschreiben kann. Es ist jedoch offensichtlich, dass die T _max Die vom aktuellen Modell berechneten Werte sind niedriger als die von der Simulation vorhergesagten, und dieser Unterschied wird mit zunehmendem Stromverbrauch deutlicher. Um diesen Mechanismus zu zeigen, simuliertes T _int werden mit zunehmender Leistung extrahiert und mit berechneten T . verglichen _int nach Gl. (10) wie in Abb. 5 aufgetragen. Es zeigt sich, dass die Joulesche Erwärmung in der Mitte des Geräts konzentrierter wird als P steigt. Es gibt 0,5 K und 4 K ΔT zwischen Modell und Simulation an dieser Stelle, wenn P = 0,25 bzw. 1 W/mm. Aus diesem Grund kann unser Modell T . nicht genau vorhersagen _max . Daher ist eine vernünftigere Hypothese von T _int wird benötigt, um in Zukunft eine höhere Genauigkeit zu erreichen. Trotzdem ist das T _max wird vom Modell vorhergesagt, dass es sogar unter einer Verlustleistungsdichte von 1 W/mm nur um  < 4 K niedriger ist als durch Simulation. Das heißt, obwohl die Hypothese des einheitlichen T _int nicht mit den Tatsachen übereinstimmt, kann unser Modell eine Schätzung von T . liefern _max mit ausreichender Genauigkeit.

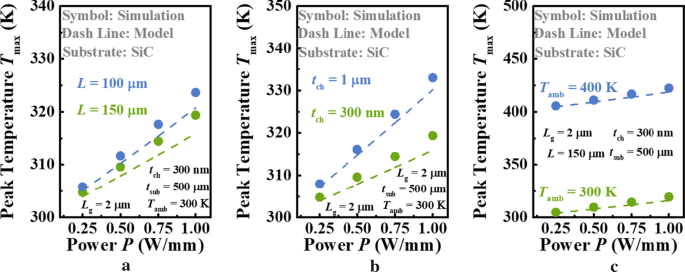
Abhängigkeit von T _max von Ga₂ O₃ MOSFETs mit SiC-Substrat auf a die Länge des Geräts L , b die Dicke von Ga₂ O₃ Schicht t _ch , und c Umgebungstemperatur T _amb bei unterschiedlicher Leistung P . Symbole und Linien kennzeichnen die Ergebnisse des vorgeschlagenen Modells bzw. der Simulation

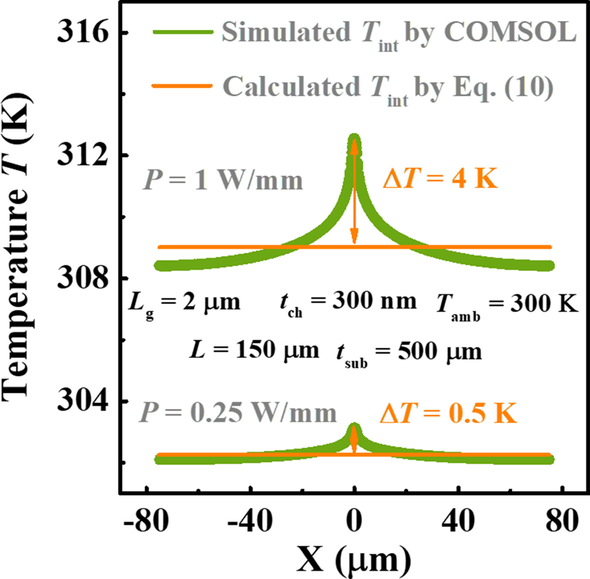
Vergleich von T _int zwischen simuliert und berechnet nach Gl. (10) an verschiedenen P

Schlussfolgerungen

Ein genaues analytisches Modell zur Schätzung des T _max von Ga₂ O₃ MOSFETs mit temperatur- und richtungsabhängiger Wärmeleitfähigkeit werden vorgestellt. Ein einfacher Ausdruck basierend auf Gerätegeometrie und Materialparametern wurde abgeleitet. Eine ausgezeichnete Übereinstimmung wurde zwischen dem Modell und den numerischen Simulationen von COMSOL Multiphysics durch Variation unterschiedlicher Leistungsaufnahme erzielt. Das vorgeschlagene Modell für die T _max ist von großer Bedeutung für effektive Wärmemanagement-Leistungsgeräte, insbesondere Ga₂ O₃ MOSFETs.

Verfügbarkeit von Daten und Materialien

Die Datensätze, die die Schlussfolgerungen dieses Artikels unterstützen, sind im Artikel enthalten.

Abkürzungen

Ga₂ O₃ :

Galliumoxid

MOSFETs:

Metall-Oxid-Halbleiter-Feldeffekttransistoren

AlGaN:

Aluminiumgalliumnitrid

GaN:

Galliumnitrid

SiC:

Siliziumkarbid