Umrechnung von Dezimalzahlen

Da oktale und hexadezimale Zahlensysteme Basen haben, die ein Vielfaches von binär sind (Basis 2), ist die Konvertierung zwischen hexadezimal oder oktal und binär sehr einfach.

Da wir mit dem Dezimalsystem so vertraut sind, ist die Umwandlung von binärer, oktaler oder hexadezimaler in dezimale Form relativ einfach (addieren Sie einfach die Produkte von Chiffrierwerten und Stellengewichten).

Die Umrechnung von Dezimalzahlen in eines dieser „seltsamen“ Zahlensysteme ist jedoch eine andere Sache.

Trial-and-Fit-Methode

Die Methode, die wahrscheinlich am sinnvollsten ist, ist die „Trial-and-Fit“-Methode, bei der Sie versuchen, die binäre, oktale oder hexadezimale Notation an den gewünschten Wert in Dezimalform „anzupassen“.

Nehmen wir zum Beispiel an, ich wollte den Dezimalwert von 87 in binärer Form darstellen. Beginnen wir damit, ein binäres Zahlenfeld zu zeichnen, komplett mit Werten für die Stellengewichtung:

Nun, wir wissen, dass wir kein "1"-Bit an der Stelle von 128 haben werden, da wir damit sofort einen Wert größer als 87 erhalten würden.

Da jedoch die nächste Gewichtung rechts (64) kleiner als 87 ist, wissen wir, dass wir dort eine „1“ haben müssen.

Würden wir auch die nächste Stelle rechts eine „1“ machen, wäre unser Gesamtwert 64₁₀ + 32₁₀ , oder 96₁₀ . Dies ist größer als 87₁₀ , also wissen wir, dass dieses Bit eine „0“ sein muss.

Wenn wir das nächste (16er) Stellenbit gleich „1“ machen, bringt dies unseren Gesamtwert auf 64₁₀ + 16₁₀ , oder 80₁₀ , was unserem gewünschten Wert näher kommt (87₁₀ ) ohne es zu überschreiten:

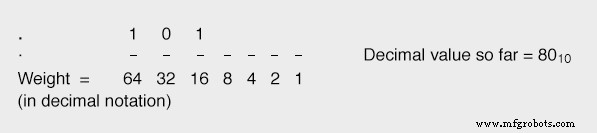
Indem wir diese Schritte fortsetzen und jedes Bit mit geringerem Gewicht so einstellen, dass wir unseren gewünschten Gesamtwert erreichen müssen, ohne ihn zu überschreiten, werden wir schließlich den richtigen Wert erhalten:

Trial-and-Fit-Methode in Oktal und Hexadezimal

Diese Trial-and-Fit-Strategie funktioniert auch mit oktalen und hexadezimalen Konvertierungen. Nehmen wir dieselbe Dezimalzahl, 87₁₀ , und wandeln Sie es in die Oktalnummer um:

Wenn wir eine Ziffer von „1“ an die Stelle von 64 setzen, hätten wir einen Gesamtwert von 64₁₀ (weniger als 87₁₀ ). Wenn wir eine Ziffer von „2“ an die Stelle von 64 setzen, hätten wir einen Gesamtwert von 128₁₀ (größer als 87₁₀ ). Dies sagt uns, dass unsere oktale Nummerierung mit einer „1“ an der Stelle der 64 beginnen muss:

Jetzt müssen wir mit Chiffrierwerten an der Stelle der 8 experimentieren, um einen Gesamtwert (Dezimalwert) so nahe wie möglich an 87 zu erhalten, ohne ihn zu überschreiten. Wenn wir die ersten Verschlüsselungsoptionen ausprobieren, erhalten wir:

Ein Chiffrierwert von „3“ anstelle der 8 würde uns über die gewünschte Summe von 87₁₀ bringen , also „2“ ist es!

Wenn Sie im letzten Abschnitt über Oktal/Binär-Umwandlungen aufgepasst haben, werden Sie natürlich feststellen, dass wir die binäre Darstellung von (dezimal) 87₁₀ . annehmen können , die wir zuvor mit 1010111₂ ermittelt haben , und konvertieren Sie es einfach in Oktal, um unsere Arbeit zu überprüfen:

Können wir die Dezimal-zu-Hexadezimal-Konvertierung auf die gleiche Weise durchführen? Klar, aber wer möchte das schon? Diese Methode ist einfach zu verstehen, aber mühsam durchzuführen.

Es gibt einen anderen Weg, diese Konvertierungen durchzuführen, der im Wesentlichen (mathematisch) gleich ist, aber einfacher zu bewerkstelligen ist.

Wiederholungsteilungstechnik

Diese andere Methode verwendet wiederholte Divisionszyklen (mit dezimaler Notation), um die dezimale Nummerierung in Vielfache von binären, oktalen oder hexadezimalen Stellenwertwerten zu zerlegen.

Im ersten Teilungszyklus nehmen wir die ursprüngliche Dezimalzahl und dividieren sie durch die Basis des Zahlensystems, in das wir konvertieren (binär=2 oktal=8, hex=16).

Dann nehmen wir den ganzzahligen Teil des Divisionsergebnisses (Quotient) und dividieren ihn erneut durch den Basiswert usw., bis wir am Ende einen Quotienten kleiner als 1 haben.

Die binären, oktalen oder hexadezimalen Ziffern werden durch die „Reste“ bestimmt, die bei jedem Divisionsschritt übrig bleiben. Sehen wir uns an, wie dies für Binärdateien funktioniert, mit dem Dezimalbeispiel von 87₁₀ :

Die Binärbits werden aus den Resten der aufeinanderfolgenden Divisionsschritte zusammengesetzt, beginnend mit dem LSB und fortschreitend zum MSB. In diesem Fall erhalten wir eine binäre Notation von 1010111₂ .

Wenn wir durch 2 dividieren, erhalten wir immer einen Quotienten, der entweder mit „.0“ oder „.5“ endet, dh einen Rest von entweder 0 oder 1. Wie bereits erwähnt, funktioniert diese wiederholte Divisionstechnik für die Konvertierung für die Numerierung andere als binäre Systeme.

Wenn wir aufeinanderfolgende Divisionen mit einer anderen Zahl durchführen, z. B. 8 für die Umwandlung in Oktal, erhalten wir notwendigerweise Reste zwischen 0 und 7. Versuchen wir es mit derselben Dezimalzahl, 87₁₀ :

Wir können eine ähnliche Technik auch zum Umwandeln von Zahlensystemen verwenden, die mit Mengen kleiner als 1 arbeiten.

Um eine Dezimalzahl kleiner als 1 in eine Binär-, Oktal- oder Hexadezimalzahl umzuwandeln, verwenden wir wiederholte Multiplikationen, wobei der ganzzahlige Teil des Produkts in jedem Schritt als nächste Ziffer unserer umgewandelten Zahl verwendet wird.

Nehmen wir die Dezimalzahl 0.8125₁₀ als Beispiel die Konvertierung in Binär:

Wie beim wiederholten Divisionsprozess für ganze Zahlen gibt uns jeder Schritt die nächste Ziffer (oder das nächste Bit), die weiter vom „Punkt“ entfernt ist.

Bei Integer (Division) arbeiteten wir vom LSB zum MSB (von rechts nach links), aber bei wiederholter Multiplikation arbeiteten wir von links nach rechts.

Um eine Dezimalzahl größer als 1 mit einer Komponente <1 umzuwandeln, müssen wir beide . verwenden Techniken, eine nach der anderen. Nehmen Sie das Dezimalbeispiel 54,40625₁₀ , in binär umwandeln:

VERWANDTE ARBEITSBLÄTTER:

• Arbeitsblatt für Zahlensysteme