Analysetechniken für seriell parallele Widerstandsschaltungen
Richtlinien für die Analyse von seriell-parallelen Kombinationsschaltungen
Das Ziel der Reihen-Parallel-Widerstandsschaltungsanalyse ist es, alle Spannungsabfälle, Ströme und Verlustleistungen in einer Schaltung bestimmen zu können. Die allgemeine Strategie, um dieses Ziel zu erreichen, ist wie folgt:
- Schritt 1: Bewerten Sie, welche Widerstände in einem Stromkreis einfach in Reihe oder einfach parallel geschaltet sind.
- Schritt 2: Zeichnen Sie den Stromkreis neu und ersetzen Sie jede dieser Reihen- oder Parallelwiderstandskombinationen, die in Schritt 1 identifiziert wurden, durch einen einzelnen äquivalenten Widerstand. Wenn Sie eine Tabelle zum Verwalten von Variablen verwenden, erstellen Sie für jedes Widerstandsäquivalent eine neue Tabellenspalte.
- Schritt 3: Wiederholen Sie die Schritte 1 und 2, bis die gesamte Schaltung auf einen äquivalenten Widerstand reduziert ist.
- Schritt 4: Gesamtstrom aus Gesamtspannung und Gesamtwiderstand berechnen (I=E/R).
- Schritt 5: Gehen Sie unter Verwendung der Gesamtspannungs- und Gesamtstromwerte zurück zum letzten Schritt des Schaltungsreduzierungsprozesses und fügen Sie diese Werte gegebenenfalls ein.
- Schritt 6: Verwenden Sie das Ohmsche Gesetz, um aus bekannten Widerständen und Gesamtspannungs-/Gesamtstromwerten aus Schritt 5 unbekannte Werte (Spannung oder Strom) zu berechnen (E=IR oder I=E/R).
- Schritt 7: Wiederholen Sie die Schritte 5 und 6, bis alle Werte für Spannung und Strom in der ursprünglichen Schaltungskonfiguration bekannt sind. Im Wesentlichen gehen Sie Schritt für Schritt von der vereinfachten Version der Schaltung zurück in ihre ursprüngliche, komplexe Form, wobei Sie gegebenenfalls die Werte von Spannung und Strom einstecken, bis alle Werte von Spannung und Strom bekannt sind.
- Schritt 8: Berechnen Sie die Verlustleistung aus bekannten Spannungs-, Strom- und/oder Widerstandswerten.
Beispiel für eine seriell-parallele Kombinationsschaltungsanalyse
Dies mag einschüchternd klingen, ist aber durch Beispiele viel einfacher zu verstehen als durch Beschreibungen.
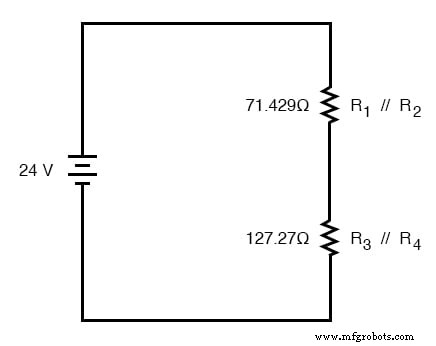

Berechnung von Parallelwiderständen
In der obigen Beispielschaltung ist R1 und R2 sind in einfacher Parallelschaltung geschaltet, ebenso wie R3 und R4 . Nachdem diese Abschnitte identifiziert wurden, müssen sie in äquivalente Einzelwiderstände umgewandelt und die Schaltung neu gezeichnet werden:

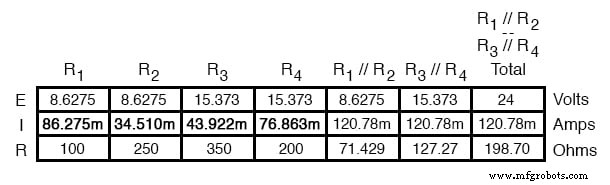
Die Doppelstrich-Symbole (//) stehen für „parallel“, um zu zeigen, dass die äquivalenten Widerstandswerte mit der Formel 1/(1/R) berechnet wurden. Der 71,429--Widerstand am oberen Ende der Schaltung entspricht R1 und R2 parallel zueinander. Der 127,27 Ω Widerstand unten entspricht R3 und R4 parallel zueinander.
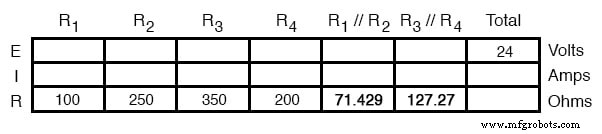
Unsere Tabelle kann erweitert werden, um diese Widerstandsäquivalente in eigene Spalten aufzunehmen:
Es sollte nun klar sein, dass die Schaltung auf eine einfache Reihenschaltung mit nur zwei (äquivalenten) Widerständen reduziert wurde. Der letzte Schritt bei der Reduzierung besteht darin, diese beiden Widerstände zu addieren, um einen Gesamtwiderstand der Schaltung zu erhalten. Wenn wir diese beiden äquivalenten Widerstände addieren, erhalten wir einen Widerstand von 198,70 Ω.
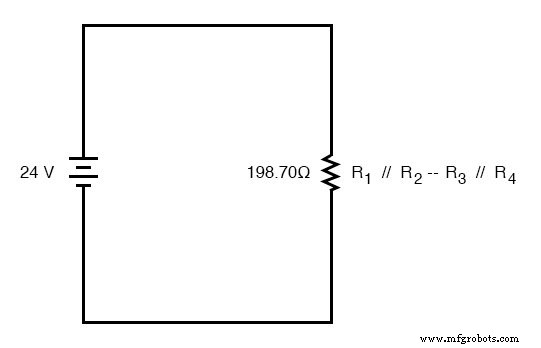
Jetzt können wir die Schaltung als einzelnen äquivalenten Widerstand neu zeichnen und die Gesamtwiderstandszahl zur ganz rechten Spalte unserer Tabelle hinzufügen. Beachten Sie, dass die Spalte "Gesamt" umbenannt wurde (R1 //R2 —R3 //R4 ), um anzugeben, in welchem Verhältnis sie zu den anderen Zahlenkolonnen steht. Das Symbol „—“ wird hier verwendet, um „Serie“ darzustellen, genauso wie das Symbol „//“ verwendet wird, um „Parallel“ darzustellen.
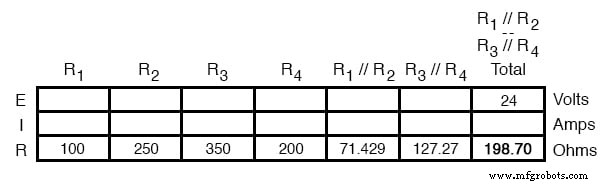
Berechnung von Strom und Spannung
Jetzt kann der Gesamtstrom des Stromkreises durch Anwendung des Ohmschen Gesetzes (I=E/R) auf die Spalte „Gesamt“ in der Tabelle bestimmt werden:
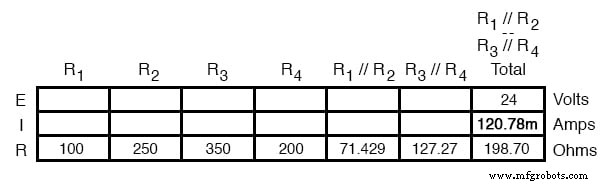
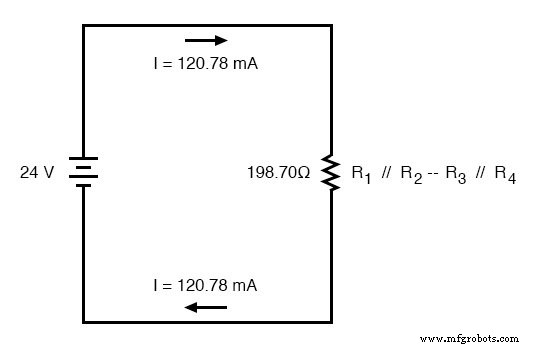
Zurück zu unserer Ersatzschaltbildzeichnung, hier wird unser Gesamtstromwert von 120,78 Milliampere als einziger Strom angezeigt:
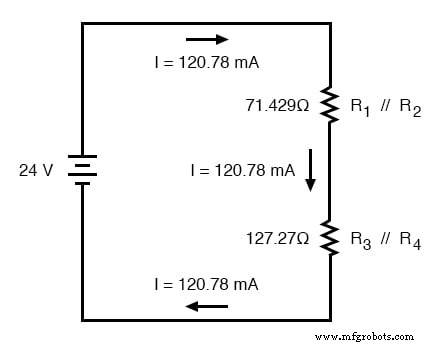
Jetzt fangen wir an, in unserem Fortschritt der Schaltungsneuzeichnungen rückwärts zur ursprünglichen Konfiguration zu arbeiten. Der nächste Schritt besteht darin, zu der Schaltung zu gehen, in der R1 //R2 und R3 //R4 sind in Serie:
Da R1 //R2 und R3 //R4 in Reihe geschaltet sind, muss der Strom durch diese beiden Sätze äquivalenter Widerstände gleich sein. Außerdem muss der durch sie fließende Strom gleich dem Gesamtstrom sein, damit wir unsere Tabelle mit den entsprechenden Stromwerten ausfüllen können, indem wir einfach den Stromwert aus der Summe-Spalte in den R1 kopieren //R2 und R3 //R4 Spalten:
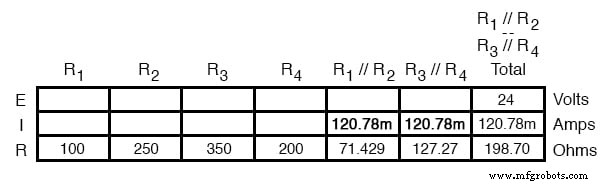
Jetzt den Strom durch die äquivalenten Widerstände R1 . kennen //R2 und R3 //R4 , können wir das Ohmsche Gesetz (E=IR) auf die beiden rechten vertikalen Spalten anwenden, um Spannungsabfälle über ihnen zu finden:
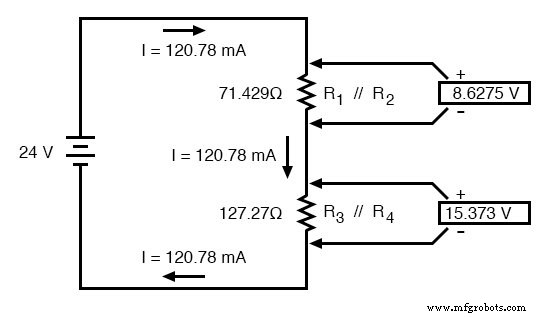
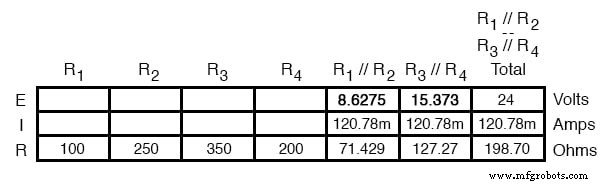
Weil wir R1 . kennen //R2 und R3 //R4 Parallelwiderstandsäquivalente sind und wir wissen, dass die Spannungsabfälle in Parallelschaltungen gleich sind, können wir die jeweiligen Spannungsabfälle in die entsprechenden Tabellenspalten für diese einzelnen Widerstände übertragen. Mit anderen Worten, wir gehen in unserer Zeichenfolge einen weiteren Schritt zurück zur ursprünglichen Konfiguration und vervollständigen die Tabelle entsprechend:
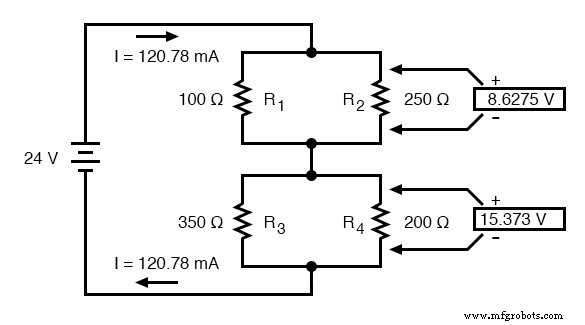
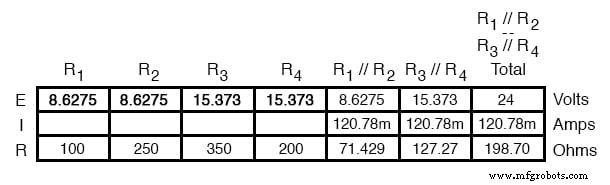
Schließlich der ursprüngliche Abschnitt der Tabelle (Spalten R1 bis R4 ) ist mit genügend Werten abgeschlossen, um den Vorgang abzuschließen. Durch Anwendung des Ohmschen Gesetzes auf die verbleibenden vertikalen Spalten (I=E/R) können wir die Ströme durch R1 . bestimmen , R2 , R3 , und R4 einzeln:
Einfügen von Spannungs- und Stromwerten in Diagramme
Nachdem wir alle Spannungs- und Stromwerte für diese Schaltung gefunden haben, können wir diese Werte im Schaltplan als solche anzeigen:
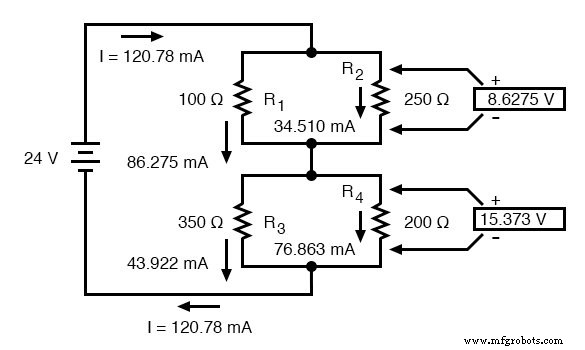
Als letzte Kontrolle unserer Arbeit können wir sehen, ob sich die berechneten Stromwerte wie gewünscht zur Summe addieren. Da R1 und R2 parallel sind, sollten sich ihre kombinierten Ströme auf insgesamt 120,78 mA summieren. Ebenso, da R3 und R4 parallel sind, sollten ihre kombinierten Ströme ebenfalls 120,78 mA ergeben. Sie können selbst überprüfen, ob sich diese Zahlen wie erwartet addieren.
Verwenden von SPICE zum Überprüfen berechneter Werte
Eine Computersimulation kann auch verwendet werden, um die Genauigkeit dieser Zahlen zu überprüfen. Die folgende SPICE-Analyse zeigt alle Widerstandsspannungen und -ströme (beachten Sie die strommessenden vi1, vi2, . . . „Dummy“-Spannungsquellen in Reihe mit jedem Widerstand in der Netzliste, die für das SPICE-Computerprogramm erforderlich sind, um den Strom durch jeden Pfad zu verfolgen ). Diese Spannungsquellen werden auf Werte von jeweils null Volt eingestellt, damit sie die Schaltung in keiner Weise beeinflussen.
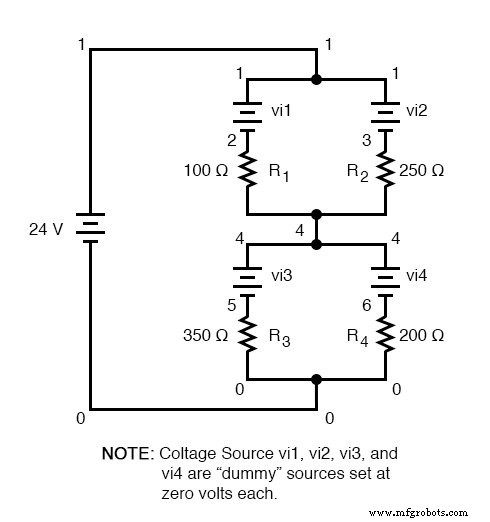
Ich habe die Ausgabezahlen von SPICE mit Anmerkungen versehen, um sie besser lesbar zu machen, und gibt an, welche Spannungs- und Stromzahlen zu welchen Widerständen gehören.
Wie Sie sehen, stimmen alle Zahlen mit den berechneten Werten überein.
RÜCKBLICK:
- Um eine Reihen-Parallel-Kombinationsschaltung zu analysieren, gehen Sie wie folgt vor:
- Reduzieren Sie die ursprüngliche Schaltung auf einen einzelnen äquivalenten Widerstand und zeichnen Sie die Schaltung in jedem Reduktionsschritt neu, da einfache Serien- und einfache parallele Teile auf einzelne äquivalente Widerstände reduziert werden.
- Löse den Gesamtwiderstand auf.
- Auflösen nach Gesamtstrom (I=E/R).
- Bestimmen Sie äquivalente Widerstandsspannungsabfälle und verzweigen Sie Ströme stufenweise, indem Sie wieder rückwärts zur ursprünglichen Schaltungskonfiguration arbeiten.
VERWANDTE ARBEITSBLÄTTER:
- Arbeitsblatt algebraische Gleichungsmanipulation für elektrische Schaltkreise
- Arbeitsblatt für seriellparallele Gleichstromkreise
Industrietechnik



