Einfache Serienschaltungen

Auf dieser Seite skizzieren wir die drei Prinzipien, die Sie in Bezug auf Reihenschaltungen verstehen sollten:

1. Aktuell :Die Strommenge ist durch jede Komponente in einer Reihenschaltung gleich.
2. Widerstand :Der Gesamtwiderstand einer Reihenschaltung ist gleich der Summe der Einzelwiderstände.
3. Spannung :Die Versorgungsspannung in einer Reihenschaltung ist gleich der Summe der einzelnen Spannungsabfälle.

Schauen wir uns einige Beispiele für Reihenschaltungen an, die diese Prinzipien demonstrieren.

Wir beginnen mit einer Reihenschaltung aus drei Widerständen und einer einzelnen Batterie:

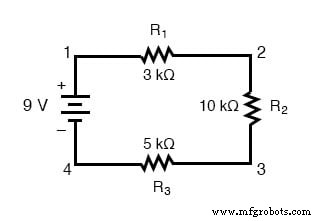
Das erste Prinzip, das Sie bei Reihenschaltungen verstehen müssen, ist wie folgt:

Die Strommenge in einer Reihenschaltung ist durch alle Komponenten in der Schaltung gleich.

Dies liegt daran, dass es in einer Reihenschaltung nur einen Pfad für den Stromfluss gibt. Da elektrische Ladung durch Leiter wie Murmeln in einer Röhre fließt, muss die Flussrate (Marmorgeschwindigkeit) an jedem Punkt im Stromkreis (Röhre) zu einem bestimmten Zeitpunkt gleich sein.

Verwendung des Ohmschen Gesetzes in Reihenschaltungen

An der Anordnung der 9-Volt-Batterie können wir erkennen, dass der Strom in diesem Stromkreis im Uhrzeigersinn von Punkt 1 zu 2 zu 3 zu 4 und zurück zu 1 fließt. Wir haben jedoch eine Spannungsquelle und drei Widerstände. Wie verwenden wir hier das Ohmsche Gesetz?

Eine wichtige Einschränkung des Ohmschen Gesetzes ist, dass sich alle Größen (Spannung, Strom, Widerstand und Leistung) in Bezug auf dieselben zwei Punkte in einem Stromkreis aufeinander beziehen müssen. Wir können dieses Konzept im folgenden Beispiel einer Einzelwiderstandsschaltung in Aktion sehen.

Verwendung des Ohmschen Gesetzes in einer einfachen Einzelwiderstandsschaltung

Mit einer Einzelbatterie- und Einzelwiderstandsschaltung könnten wir leicht jede Menge berechnen, da sie alle auf die gleichen zwei Punkte in der Schaltung angewendet wurden:

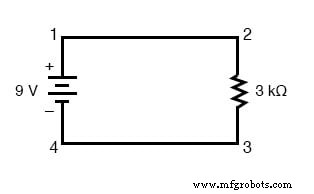
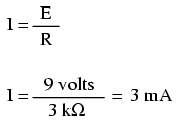
Da die Punkte 1 und 2 ebenso wie die Punkte 3 und 4 durch den Draht mit vernachlässigbarem Widerstand miteinander verbunden sind, können wir sagen, dass Punkt 1 elektrisch mit Punkt 2 und Punkt 3 elektrisch mit Punkt 4 gemeinsam ist 9 Volt elektromotorische Kraft zwischen den Punkten 1 und 4 (direkt über der Batterie) haben, und da Punkt 2 gemeinsam mit Punkt 1 und Punkt 3 gemeinsam mit Punkt 4 ist, müssen wir auch 9 Volt zwischen den Punkten 2 und 3 (direkt über der Batterie) haben Widerstand).

Daher können wir das Ohmsche Gesetz (I =E/R) auf den Strom durch den Widerstand anwenden, da wir die Spannung (E) am Widerstand und den Widerstand (R) dieses Widerstands kennen. Alle Terme (E, I, R) gelten für dieselben zwei Punkte in der Schaltung, für denselben Widerstand, daher können wir die Formel des Ohmschen Gesetzes ohne Vorbehalt verwenden.

Verwendung des Ohmschen Gesetzes in Schaltungen mit mehreren Widerständen

Bei Schaltungen mit mehr als einem Widerstand müssen wir bei der Anwendung des Ohmschen Gesetzes vorsichtig sein. In der folgenden Beispielschaltung mit drei Widerständen wissen wir, dass wir zwischen den Punkten 1 und 4 9 Volt haben, was der Menge der elektromotorischen Kraft entspricht, die den Strom durch die Reihenkombination von R₁ . treibt , R₂ , und R₃ . Wir können jedoch nicht den Wert von 9 Volt nehmen und ihn durch 3k, 10k oder 5k Ω dividieren, um zu versuchen, einen Stromwert zu finden, da wir nicht wissen, wie viel Spannung an jedem dieser Widerstände einzeln anliegt.

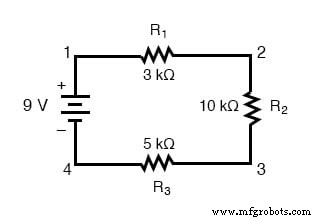
Die Zahl von 9 Volt ist eine Summe Menge für die gesamte Schaltung, während die Zahlen von 3k, 10k und 5k Ω individuell . sind Mengen für einzelne Widerstände. Wenn wir eine Zahl für die Gesamtspannung in eine Gleichung des Ohmschen Gesetzes mit einer Zahl für den Einzelwiderstand einsetzen würden, würde sich das Ergebnis nicht genau auf eine Größe in der realen Schaltung beziehen.

Für R₁ , das Ohmsche Gesetz bezieht sich auf die Höhe der Spannung an R₁ mit dem Strom durch R₁ , gegeben R₁ Widerstand, 3kΩ:

Da wir jedoch die Spannung an R₁ nicht kennen, (nur die Gesamtspannung, die von der Batterie über die Drei-Widerstands-Reihenkombination geliefert wird) und wir kennen den Strom durch R₁ . nicht , können wir mit beiden Formeln keine Berechnungen durchführen. Das gleiche gilt für R₂ und R₃ :Wir können die Gleichungen des Ohmschen Gesetzes genau dann anwenden, wenn alle Terme für ihre jeweiligen Größen zwischen denselben zwei Punkten in der Schaltung repräsentativ sind.

Also was können wir tun? Wir kennen die Spannung der Quelle (9 Volt), die über die Reihenkombination von R₁ . angelegt wird , R₂ , und R₃ , und wir kennen den Widerstand jedes Widerstands, aber da diese Größen nicht im gleichen Kontext stehen, können wir das Ohmsche Gesetz nicht verwenden, um den Stromkreis zu bestimmen. Wenn wir nur wüssten, was die Gesamtzahl ist Widerstand war für die Schaltung:dann könnten wir die Gesamtzahl . berechnen aktuell mit unserer Zahl für Gesamt Spannung (I=E/R).

Kombinieren mehrerer Widerstände zu einem äquivalenten Gesamtwiderstand

Damit kommen wir zum zweiten Prinzip der Reihenschaltung:

Der Gesamtwiderstand jeder Reihenschaltung ist gleich der Summe der Einzelwiderstände.

Dies sollte intuitiv sinnvoll sein:Je mehr Widerstände in Reihe geschaltet werden müssen, desto schwieriger wird der Stromfluss.

Im Beispielproblem hatten wir 3 kΩ, 10 kΩ und 5 kΩ Widerstände in Reihe, was uns einen Gesamtwiderstand von 18 kΩ ergibt:

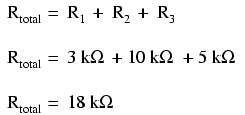
Im Wesentlichen haben wir den äquivalenten Widerstand von R₁ . berechnet , R₂ , und R₃ kombiniert. Wenn wir dies wissen, könnten wir die Schaltung mit einem einzigen Ersatzwiderstand neu zeichnen, der die Reihenkombination von R₁ . darstellt , R₂ , und R₃ :

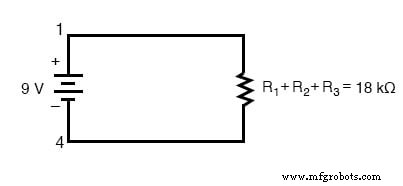
Berechnung des Stromkreises mit dem Ohmschen Gesetz

Jetzt haben wir alle notwendigen Informationen, um den Stromkreis zu berechnen, da wir die Spannung zwischen den Punkten 1 und 4 (9 Volt) und den Widerstand zwischen den Punkten 1 und 4 (18 kΩ) haben:

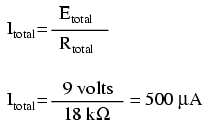
Berechnung von Komponentenspannungen mit dem Ohmschen Gesetz

Da wir wissen, dass der Strom durch alle Komponenten einer Reihenschaltung gleich ist (und wir gerade den Strom durch die Batterie bestimmt haben), können wir zu unserem ursprünglichen Schaltplan zurückkehren und den Strom durch jede Komponente notieren:

Da wir nun die Stromstärke durch jeden Widerstand kennen, können wir das Ohmsche Gesetz verwenden, um den Spannungsabfall an jedem Widerstand zu bestimmen (unter Anwendung des Ohmschen Gesetzes im richtigen Kontext):

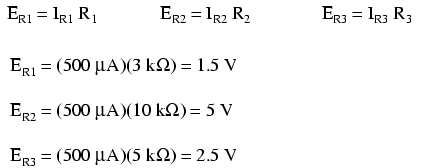
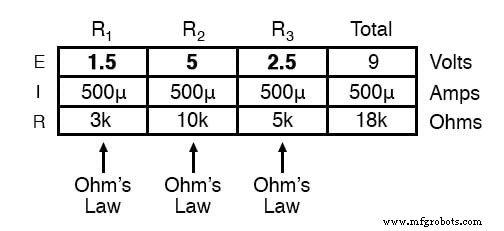
Beachten Sie die Spannungsabfälle an jedem Widerstand und wie die Summe der Spannungsabfälle (1,5 + 5 + 2,5) der Batteriespannung (Versorgungsspannung) entspricht:9 Volt.

Dies ist das dritte Prinzip der Reihenschaltung:

Die Versorgungsspannung in einer Reihenschaltung ist gleich der Summe der einzelnen Spannungsabfälle.

Analyse einfacher Reihenschaltungen mit der „Tabellenmethode“ und dem Ohmschen Gesetz

Die Methode, die wir gerade zur Analyse dieser einfachen Reihenschaltung verwendet haben, kann jedoch zum besseren Verständnis vereinfacht werden. Indem Sie eine Tabelle verwenden, um alle Spannungen, Ströme und Widerstände in der Schaltung aufzulisten, wird es sehr einfach zu sehen, welche dieser Größen in einer beliebigen Gleichung des Ohmschen Gesetzes richtig in Beziehung gesetzt werden können:

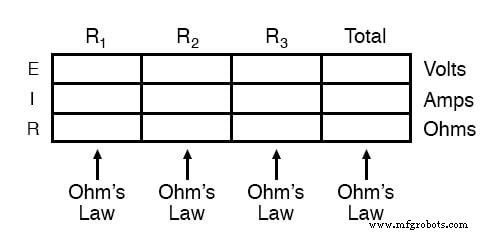
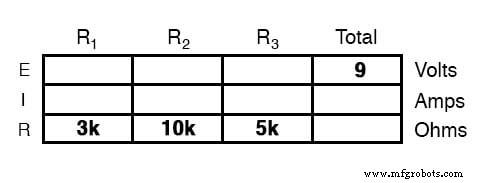
Die Regel bei einer solchen Tabelle ist, das Ohmsche Gesetz nur auf die Werte innerhalb jeder vertikalen Spalte anzuwenden. Zum Beispiel E_R1 nur mit I_R1 und R₁; E_R2 nur mit I_R2 und R₂; usw. Sie beginnen Ihre Analyse, indem Sie die Elemente der Tabelle ausfüllen, die Ihnen von Anfang an gegeben wurden:

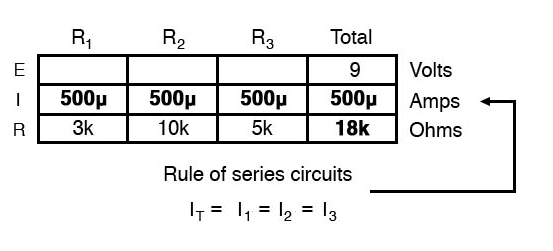
Wie Sie an der Anordnung der Daten sehen können, können wir die 9 Volt ET (Gesamtspannung) an keinen der Widerstände (R₁ .) anlegen , R₂ , oder R₃ ) in einer Formel des Ohmschen Gesetzes, weil sie in verschiedenen Spalten sind. Die 9 Volt Batteriespannung sind nicht direkt auf R₁ . angewendet , R₂ , oder R₃ . Wir können jedoch unsere „Regeln“ für Reihenschaltungen verwenden, um leere Stellen in einer horizontalen Reihe auszufüllen. In diesem Fall können wir mit der Reihenregel der Widerstände einen Gesamtwiderstand aus der Summe . ermitteln der Einzelwiderstände:

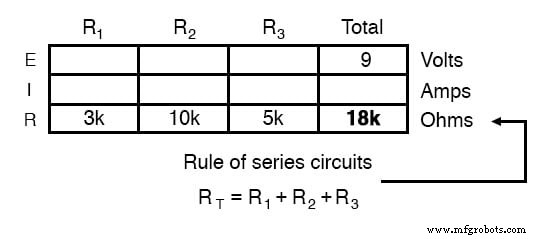
Nun, mit einem Wert für den Gesamtwiderstand, der in die Spalte ganz rechts ("Total") eingefügt ist, können wir das Ohmsche Gesetz von I=E/R auf die Gesamtspannung und den Gesamtwiderstand anwenden, um einen Gesamtstrom von 500 µA zu erhalten:

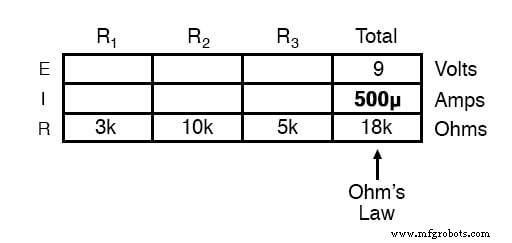
Da wir dann wissen, dass der Strom von allen Komponenten einer Reihenschaltung gleichmäßig geteilt wird (eine weitere „Regel“ von Reihenschaltungen), können wir die Ströme für jeden Widerstand aus der gerade berechneten Stromzahl eingeben:

Schließlich können wir das Ohmsche Gesetz verwenden, um den Spannungsabfall an jedem Widerstand spaltenweise zu bestimmen:

Berechnungen mit Computeranalyse (SPICE) überprüfen

Nur zum Spaß können wir einen Computer verwenden, um genau diese Schaltung automatisch zu analysieren. Es wird eine gute Möglichkeit sein, unsere Berechnungen zu überprüfen und sich auch mit der Computeranalyse vertraut zu machen. Zuerst müssen wir dem Computer die Schaltung in einem von der Software erkennbaren Format beschreiben.

Das SPICE-Programm, das wir verwenden werden, erfordert, dass alle elektrisch eindeutigen Punkte in einer Schaltung nummeriert sind, und die Komponentenplatzierung wird dadurch verstanden, welche dieser nummerierten Punkte oder „Knoten“ sie gemeinsam haben. Aus Gründen der Übersichtlichkeit habe ich die vier Ecken unserer Beispielschaltung 1 bis 4 nummeriert. SPICE verlangt jedoch, dass es irgendwo in der Schaltung einen Nullpunkt gibt, also werde ich die Schaltung neu zeichnen und das Nummerierungsschema leicht ändern:

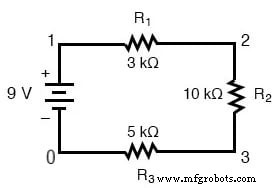
Ich habe hier nur die untere linke Ecke der Schaltung mit 0 statt mit 4 neu nummeriert. Jetzt kann ich mehrere Textzeilen in eine Computerdatei eingeben, die die Schaltung in Begriffen beschreibt, die SPICE versteht, komplett mit ein paar zusätzliche Codezeilen, die das Programm anweisen, Spannungs- und Stromdaten für unser Sehvergnügen anzuzeigen. Diese Computerdatei ist als Netzliste bekannt in SPICE-Terminologie:

Reihenschaltung v1 1 0 r1 1 2 3k r2 2 3 10k r3 3 0 5k .dc v1 9 9 1 .print dc v(1,2) v(2,3) v(3,0) .Ende

Jetzt muss ich nur noch das SPICE-Programm ausführen, um die Netzliste zu verarbeiten und die Ergebnisse auszugeben:

v1 v(1,2) v(2,3) v(3) i(v1) 9.000E+001.500E+005.000E+002.500E+00-5.000E-04

Dieser Ausdruck sagt uns, dass die Batteriespannung 9 Volt beträgt und die Spannung über R₁ . abfällt , R₂ , und R₃ sind 1,5 Volt, 5 Volt bzw. 2,5 Volt. Spannungsabfälle über jede Komponente in SPICE werden durch die Knotennummern referenziert, zwischen denen die Komponente liegt, also bezieht sich v(1,2) auf die Spannung zwischen den Knoten 1 und 2 in der Schaltung, das sind die Punkte zwischen denen R₁ befindet.

Die Reihenfolge der Knotennummern ist wichtig:Wenn SPICE eine Zahl für v(1,2) ausgibt, betrachtet es die Polarität genauso, als würden wir ein Voltmeter mit der roten Messleitung an Knoten 1 und der schwarzen Messleitung an Knoten . halten 2. Wir haben auch ein Display, das Strom (wenn auch mit einem negativen Wert) bei 0,5 Milliampere oder 500 Mikroampere anzeigt. Unsere mathematische Analyse wurde also vom Computer bestätigt. Diese Zahl erscheint in der SPICE-Analyse als negative Zahl, aufgrund einer Eigenart in der Art und Weise, wie SPICE mit aktuellen Berechnungen umgeht.

Zusammenfassend ist eine Reihenschaltung so definiert, dass sie nur einen Pfad hat, durch den Strom fließen kann. Aus dieser Definition folgen drei Regeln für Reihenschaltungen:Alle Komponenten teilen den gleichen Strom; Widerstände addieren sich zu einem größeren Gesamtwiderstand; und Spannungsabfälle addieren sich zu einer größeren Gesamtspannung. Alle diese Regeln finden ihren Ursprung in der Definition einer Reihenschaltung. Wenn Sie diese Definition vollständig verstehen, sind die Regeln nichts anderes als Fußnoten zur Definition.

RÜCKBLICK:

• Komponenten in einer Reihenschaltung teilen den gleichen Strom:I_Gesamt =I₁ =I₂ =. . . Ich_n
• Der Gesamtwiderstand in einer Reihenschaltung ist gleich der Summe der Einzelwiderstände:RTotal =R₁ + R₂ + . . . R_n
• Gesamtspannung in einer Reihenschaltung ist gleich der Summe der einzelnen Spannungsabfälle E_Gesamt =E₁ + E₂ + . . . En

Probieren Sie unsere Rechner für das Ohmsche Gesetz in unserem Tools Abschnitt.

VERWANDTE ARBEITSBLÄTTER:

• Arbeitsblatt zum Üben von Gleichstromkreisen mit Lösungen
• Arbeitsblatt algebraische Gleichungsmanipulation für elektrische Schaltkreise

Was sind „Serien“- und „Parallel“-Schaltungen? Einfache Parallelschaltung