Einfache Parallelschaltung
Auf dieser Seite skizzieren wir die drei Prinzipien, die Sie in Bezug auf Parallelschaltungen verstehen sollten:
- Spannung: Die Spannung ist an allen Komponenten in einer Parallelschaltung gleich.
- Aktuell: Der Gesamtstrom des Stromkreises ist gleich der Summe der einzelnen Zweigströme.
- Widerstand: Individuelle Widerstände vermindern um einen kleineren Gesamtwiderstand zu erreichen, anstatt hinzuzufügen um die Summe zu bilden.
Schauen wir uns einige Beispiele für Parallelschaltungen an, die diese Prinzipien demonstrieren.
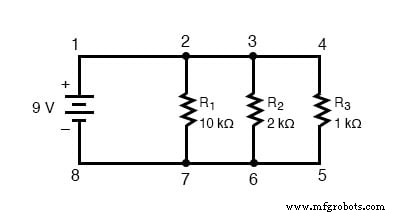
Wir beginnen mit einer Parallelschaltung aus drei Widerständen und einer einzigen Batterie:
Spannung in Parallelschaltungen
Das erste zu verstehende Prinzip bei Parallelschaltungen ist, dass die Spannung an allen Komponenten in der Schaltung gleich ist . Dies liegt daran, dass es in einer Parallelschaltung nur zwei Sätze von elektrisch gemeinsamen Punkten gibt und die zwischen den Sätzen von gemeinsamen Punkten gemessene Spannung zu jedem Zeitpunkt immer gleich sein muss.
Daher ist in der obigen Schaltung die Spannung an R1 gleich der Spannung an R2 die gleich der Spannung an R3 . ist die gleich der Spannung an der Batterie ist.
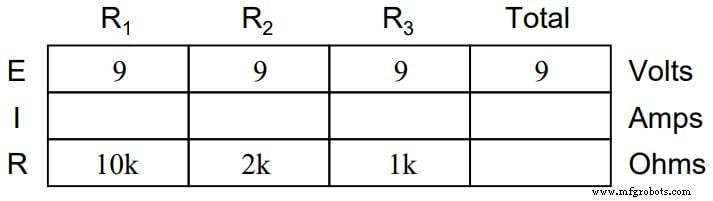
Diese Spannungsgleichheit lässt sich in einer weiteren Tabelle für unsere Startwerte darstellen:
Anwendungen des Ohmschen Gesetzes für einfache Parallelschaltungen
Genau wie bei Reihenschaltungen gilt der gleiche Vorbehalt für das Ohmsche Gesetz:Werte für Spannung, Strom und Widerstand müssen im gleichen Kontext stehen, damit die Berechnungen korrekt funktionieren.
In der obigen Beispielschaltung können wir jedoch sofort das Ohmsche Gesetz auf jeden Widerstand anwenden, um seinen Strom zu ermitteln, da wir die Spannung an jedem Widerstand (9 Volt) und den Widerstand jedes Widerstands kennen:

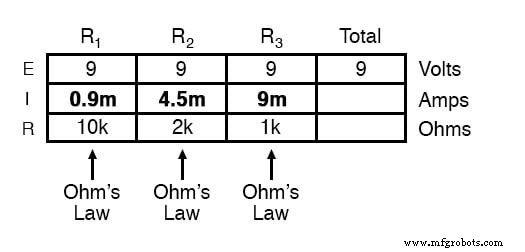
Zu diesem Zeitpunkt wissen wir immer noch nicht, wie hoch der Gesamtstrom oder der Gesamtwiderstand für diese Parallelschaltung ist, daher können wir das Ohmsche Gesetz nicht auf die ganz rechte Spalte („Gesamt“) anwenden. Wenn wir jedoch genau überlegen, was passiert, sollte klar sein, dass der Gesamtstrom der Summe aller Einzelwiderstandsströme („Zweigströme“) entsprechen muss:
Da der Gesamtstrom den Pluspol (+) der Batterie an Punkt 1 verlässt und durch den Stromkreis fließt, spaltet sich ein Teil des Stroms an Punkt 2 ab und fließt durch R1 , einige weitere spalten sich bei Punkt 3 ab, um durch R2 zu gehen , und der Rest geht durch R3 . Wie bei einem Fluss, der sich in mehrere kleinere Bäche verzweigt, müssen die kombinierten Durchflussmengen aller Bäche der Durchflussmenge des gesamten Flusses entsprechen.
Dasselbe tritt auf, wenn die Ströme durch R1 , R2 , und R3 verbinden, um zurück zum Minuspol der Batterie (-) in Richtung Punkt 8 zu fließen:der Stromfluss von Punkt 7 zu Punkt 8 muss der Summe der (Zweig-)Ströme durch R1 entsprechen , R2 , und R3 .
Dies ist das zweite Prinzip von Parallelschaltungen:Der Gesamtstrom der Schaltung ist gleich der Summe der einzelnen Zweigströme .
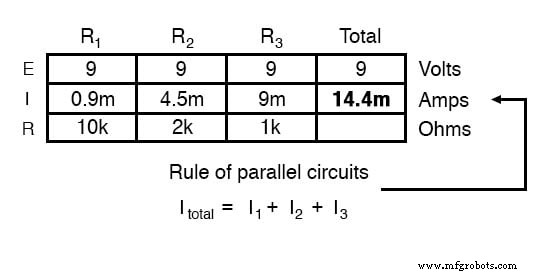
Nach diesem Prinzip können wir den IT-Spot auf unserem Tisch mit der Summe von IR1 . ausfüllen , IR2 , und ichR3 :
So berechnen Sie den Gesamtwiderstand in Parallelschaltungen
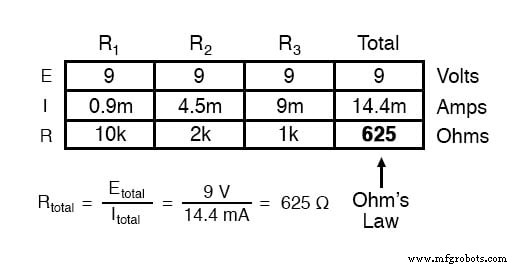
Wenn wir schließlich das Ohmsche Gesetz auf die ganz rechte Spalte („Gesamt“) anwenden, können wir den Gesamtwiderstand der Schaltung berechnen:
Die Widerstandsgleichung in Parallelschaltungen
Bitte beachten Sie hier etwas sehr Wichtiges. Der gesamte Stromkreiswiderstand beträgt nur 625 Ω:weniger als jeder der einzelnen Widerstände. In der Reihenschaltung, wo der Gesamtwiderstand die Summe der Einzelwiderstände war, war die Summe zwangsläufig größer als jeder der Widerstände einzeln.
Hier in der Parallelschaltung ist jedoch das Gegenteil der Fall:Wir sagen, dass die Einzelwiderstände verringern statt hinzufügen um die Summe zu bilden .
Dieses Prinzip vervollständigt unseren Dreiklang von „Regeln“ für Parallelschaltungen, so wie sich herausstellte, dass Reihenschaltungen drei Regeln für Spannung, Strom und Widerstand haben.
Mathematisch sieht der Zusammenhang zwischen Gesamtwiderstand und Einzelwiderständen in einer Parallelschaltung so aus:
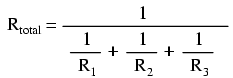
So ändern Sie die Nummerierungsschemata für Parallelschaltungen für SPICE
Die gleiche Grundform der Gleichung funktioniert für jede Anzahl der parallel geschalteten Widerstände, addieren Sie einfach so viele 1/R-Terme auf den Nenner des Bruchs wie nötig, um alle parallelen Widerstände in der Schaltung aufzunehmen.
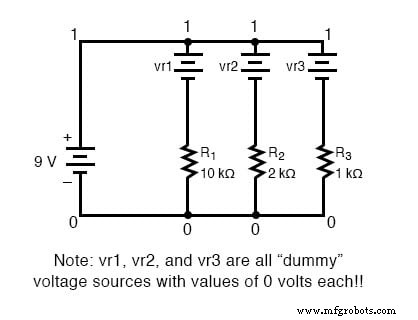
Genau wie bei der Reihenschaltung können wir unsere Berechnungen durch Computeranalysen überprüfen. Zuerst müssen wir natürlich unsere Beispielschaltung dem Computer in Begriffen beschreiben, die er verstehen kann. Ich beginne damit, die Schaltung neu zu zeichnen:

Auch hier stellen wir fest, dass das ursprüngliche Nummerierungsschema, das zur Identifizierung von Punkten in der Schaltung verwendet wurde, zugunsten von SPICE geändert werden muss.
In SPICE müssen alle elektrisch gemeinsamen Punkte identische Knotennummern haben. So weiß SPICE, was mit was und wie verbunden ist.
Bei einer einfachen Parallelschaltung liegen alle Punkte in einer von zwei Punktmengen elektrisch gemeinsam. Für unsere Beispielschaltung hat der Draht, der die Oberseiten aller Komponenten verbindet, eine Knotennummer und der Draht, der die Unterseiten der Komponenten verbindet, hat die andere.
Getreu der Konvention, Null als Knotennummer einzuschließen, wähle ich die Zahlen 0 und 1:
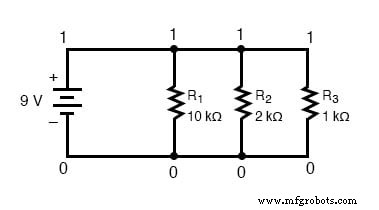
Ein Beispiel wie dieses macht die Bedeutung der Knotennummern in SPICE ziemlich klar. Dadurch, dass alle Komponenten gemeinsame Zahlensätze verwenden, „weiß“ der Computer, dass sie alle parallel miteinander verbunden sind.
Um Zweigströme in SPICE anzuzeigen, müssen wir Nullspannungsquellen in Reihe (in Reihe) mit jedem Widerstand einfügen und dann unsere Strommessungen auf diese Quellen beziehen.
Aus irgendeinem Grund haben die Macher des SPICE-Programms es so gemacht, dass der Strom nur bis . berechnet werden kann eine Spannungsquelle. Dies ist eine etwas nervige Forderung des Simulationsprogramms SPICE. Wenn jede dieser „Dummy“-Spannungsquellen hinzugefügt wird, müssen einige neue Knotennummern erstellt werden, um sie mit ihren jeweiligen Zweigwiderständen zu verbinden:

So überprüfen Sie die Ergebnisse der Computeranalyse
Die Dummy-Spannungsquellen sind alle auf 0 Volt eingestellt, um keinen Einfluss auf den Betrieb der Schaltung zu haben.
Die Schaltungsbeschreibungsdatei oder Netzliste , sieht so aus:
Parallelschaltung v1 1 0 r1 2 0 10k r2 3 0 2k r3 4 0 1k vr1 1 2 dc 0 vr2 1 3 dc 0 vr3 1 4 dc 0 .dc v1 9 9 1 .print dc v(2,0) v(3,0) v(4,0) .print dc i(vr1) i(vr2) i(vr3) .Ende
Wenn wir die Computeranalyse ausführen, erhalten wir diese Ergebnisse (ich habe den Ausdruck mit beschreibenden Etiketten versehen):
Spannung
Spannung
Diese Werte stimmen tatsächlich mit denen überein, die zuvor durch das Ohmsche Gesetz berechnet wurden:0,9 mA für IR1 , 4,5 mA für IR2 , und 9 mA für IR3 . Da sie parallel geschaltet sind, fällt natürlich an allen Widerständen die gleiche Spannung ab (9 Volt, wie bei der Batterie).
Drei Regeln für Parallelschaltungen
Zusammenfassend ist eine Parallelschaltung definiert als eine, bei der alle Komponenten zwischen denselben elektrisch gemeinsamen Punkten verbunden sind. Anders ausgedrückt:Alle Komponenten sind über die Klemmen der jeweils anderen verbunden. Aus dieser Definition folgen drei Regeln für Parallelschaltungen:
- Alle Komponenten haben dieselbe Spannung.
- Widerstände verringern sich und entsprechen einem kleineren Gesamtwiderstand.
- Zweigströme addieren sich zu einem größeren Gesamtstrom.
Wie bei Reihenschaltungen wurzeln alle diese Regeln in der Definition einer Parallelschaltung. Wenn Sie diese Definition vollständig verstehen, sind die Regeln nichts anderes als Fußnoten zur Definition.
RÜCKBLICK:
- Komponenten in einer Parallelschaltung haben dieselbe Spannung:EGesamt =E1 =E2 =. . . En
- Der Gesamtwiderstand in einer Parallelschaltung ist weniger als jeder der Einzelwiderstände:RGesamt =1 / (1/R1 + 1/R2 + . . . 1/Rn )
- Gesamtstrom in einer Parallelschaltung ist gleich der Summe der einzelnen Zweigströme:IGesamt =I1 + I2 + . . . Ichn .
VERWANDTE ARBEITSBLÄTTER:
- Übungsarbeitsblatt für parallele Gleichstromkreise mit Arbeitsblatt mit Lösungen
- Arbeitsblatt algebraische Gleichungsmanipulation für elektrische Schaltkreise
Industrietechnik



