Mesh aktuelle Methode und Analyse
Die Mesh-Current-Methode , auch bekannt als Loop Current Method , ist der Branch-Current-Methode insofern sehr ähnlich, als sie simultane Gleichungen, das Kirchhoffsche Spannungsgesetz und das Ohmsche Gesetz verwendet, um unbekannte Ströme in einem Netzwerk zu bestimmen. Es unterscheidet sich von der Branch Current-Methode dadurch, dass es nicht Verwenden Sie das Kirchhoffsche Stromgesetz, und es ist normalerweise in der Lage, eine Schaltung mit weniger unbekannten Variablen und weniger gleichzeitigen Gleichungen zu lösen, was besonders schön ist, wenn Sie gezwungen sind, ohne Taschenrechner zu lösen.
Mesh Current, konventionelle Methode
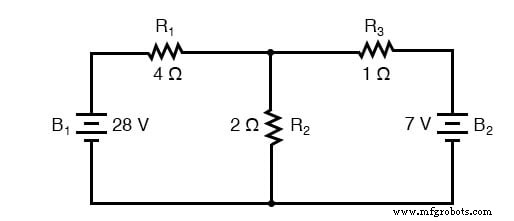
Sehen wir uns an, wie diese Methode bei demselben Beispielproblem funktioniert:
Schleifen identifizieren
Der erste Schritt bei der Mesh-Current-Methode besteht darin, „Schleifen“ innerhalb der Schaltung zu identifizieren, die alle Komponenten umfasst. In unserer Beispielschaltung ist die von B1 . gebildete Schleife , R1 , und R2 wird die erste sein, während die Schleife von B2 . gebildet wird , R2 , und R3 wird der zweite sein. Der seltsamste Teil der Mesh-Current-Methode besteht darin, sich zirkulierende Ströme in jeder der Schleifen vorzustellen. Tatsächlich hat diese Methode ihren Namen von der Idee, dass diese Ströme zwischen Schleifen wie Sätze von sich drehenden Zahnrädern ineinandergreifen:
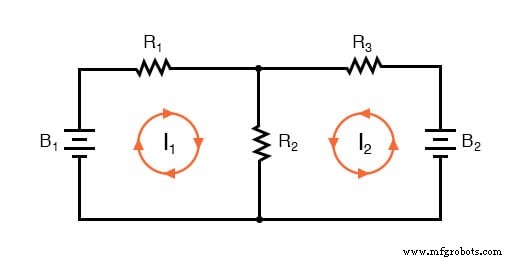
Die Wahl der Richtung jedes Stroms ist völlig willkürlich, genau wie bei der Branch Current-Methode, aber die resultierenden Gleichungen sind einfacher zu lösen, wenn die Ströme durch sich schneidende Komponenten in die gleiche Richtung fließen (beachten Sie, wie Ströme I1 und ich2 gehen beide nach oben durch den Widerstand R2 , wo sie „ineinandergreifen“ oder sich überschneiden). Wenn die angenommene Richtung eines Maschenstroms falsch ist, hat die Antwort für diesen Strom einen negativen Wert.
Beschrifte die Polaritäten des Spannungsabfalls
Der nächste Schritt besteht darin, alle Polaritäten des Spannungsabfalls an den Widerständen entsprechend den angenommenen Richtungen der Maschenströme zu beschriften. Denken Sie daran, dass das „vorgelagerte“ Ende eines Widerstands immer negativ und das „vorgelagerte“ Ende eines Widerstands positiv zueinander ist, da Elektronen negativ geladen sind. Die Batteriepolaritäten werden natürlich durch ihre Symbolorientierungen im Diagramm bestimmt und können mit den Widerstandspolaritäten (angenommene Stromrichtungen) „übereinstimmen“ oder nicht:
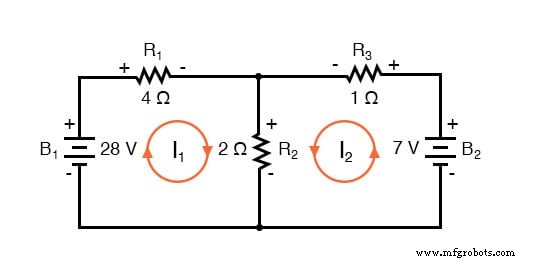
Mit dem Spannungsgesetz von Kirchhoff können wir nun jede dieser Schleifen umgehen und Gleichungen erzeugen, die die Spannungsabfälle und Polaritäten der Komponenten darstellen. Wie bei der Branch Current-Methode bezeichnen wir den Spannungsabfall eines Widerstands als Produkt des Widerstands (in Ohm) und seines jeweiligen Maschenstroms (diese Größe ist zu diesem Zeitpunkt unbekannt). Wenn zwei Ströme ineinandergreifen, schreiben wir diesen Begriff in die Gleichung, wobei der Widerstandsstrom die Summe ist der beiden Eingriffsströme.
Verfolgen der linken Schleife der Schaltung mit Gleichungen
Die linke Schleife der Strecke abfahren, ausgehend von der oberen linken Ecke und gegen den Uhrzeigersinn (die Wahl der Startpunkte und Richtungen ist letztendlich irrelevant), die Polarität zählen, als ob wir ein Voltmeter in der Hand hätten, rotes Kabel auf den Punkt vor uns und schwarzes Blei an der Spitze dahinter, erhalten wir diese Gleichung:
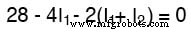
Beachten Sie, dass der mittlere Term der Gleichung die Summe der Maschenströme I1 . verwendet und ich2 als Strom durch den Widerstand R2 . Dies liegt daran, dass die Netzströme I1 und ich2 gehen in die gleiche Richtung durch R2 , und ergänzen sich somit gegenseitig. Verteilen des Koeffizienten von 2 auf I1 und ich2 Terme und dann Kombinieren von I1 Terme in der Gleichung können wir so vereinfachen:

Zu diesem Zeitpunkt haben wir eine Gleichung mit zwei Unbekannten. Um nach zwei unbekannten Maschenströmen auflösen zu können, müssen wir zwei Gleichungen haben. Wenn wir die andere Schleife der Schaltung verfolgen, können wir eine andere KVL-Gleichung erhalten und haben genügend Daten, um nach den beiden Strömen aufzulösen. Ich bin ein Gewohnheitstier, ich fange in der oberen linken Ecke der rechten Schleife an und folge gegen den Uhrzeigersinn:
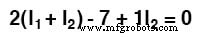
Wenn wir die Gleichung wie zuvor vereinfachen, erhalten wir:
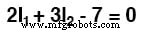
Auflösung für das Unbekannte
Mit zwei Gleichungen können wir nun eine von mehreren Methoden verwenden, um die unbekannten Ströme I1 . mathematisch aufzulösen und ich2 :

Schaltung neu zeichnen
Zu wissen, dass diese Lösungen Werte für mesh sind Ströme, nicht Zweig Ströme, müssen wir zu unserem Diagramm zurückkehren, um zu sehen, wie sie zusammenpassen, um Ströme durch alle Komponenten zu geben:
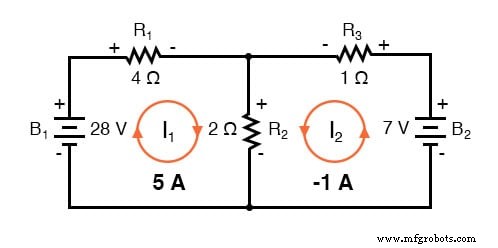
Die Lösung von -1 Ampere für I2 bedeutet, dass wir zunächst von einer falschen Stromrichtung ausgegangen sind. Tatsächlich, I2 fließt gegen den Uhrzeigersinn bei einem Wert von (positiv) 1 Ampere:
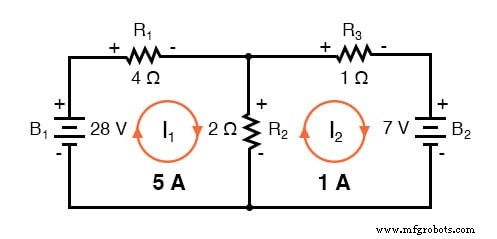
Diese Änderung der Stromrichtung gegenüber der zuerst angenommenen ändert die Polarität der Spannungsabfälle an R2 und R3 wegen Strom I2 . Von hier aus können wir sagen, dass der Strom durch R1 beträgt 5 Ampere, mit dem Spannungsabfall über R1 ist das Produkt aus Strom und Widerstand (E=IR), 20 Volt (links positiv und rechts negativ).
Außerdem können wir mit Sicherheit sagen, dass der Strom durch R3 1 Ampere, mit einem Spannungsabfall von 1 Volt (E=IR), links positiv und rechts negativ. Aber was passiert bei R2 ?
Maschenstrom I1 geht „abwärts“ durch R2 , während Maschenstrom I2 geht „aufwärts“ durch R2 . Um den tatsächlichen Strom durch R2 . zu bestimmen , wir müssen sehen, wie die Maschenströme I1 und ich2 interagieren (in diesem Fall sind sie in Opposition) und addieren sie algebraisch, um einen endgültigen Wert zu erhalten. Da ich1 geht bei 5 Ampere "ab" und I2 geht mit 1 Ampere „auf“, das echte Strom durch R2 muss ein Wert von 4 Ampere sein, nach unten gehend:
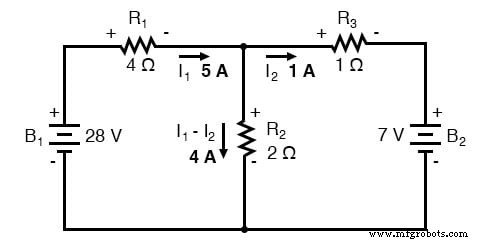
Ein Strom von 4 Ampere durch R2 Der Widerstand von 2 ergibt einen Spannungsabfall von 8 Volt (E=IR), oben positiv und unten negativ.
Vorteil der Netzstromanalyse
Der Hauptvorteil der Mesh Current-Analyse besteht darin, dass sie im Allgemeinen die Lösung eines großen Netzwerks mit weniger unbekannten Werten und weniger gleichzeitigen Gleichungen ermöglicht. Unser Beispielproblem benötigte drei Gleichungen, um die Branch Current-Methode zu lösen, und nur zwei Gleichungen, die die Mesh-Current-Methode verwendet. Dieser Vorteil ist umso größer, je komplexer die Netzwerke werden:
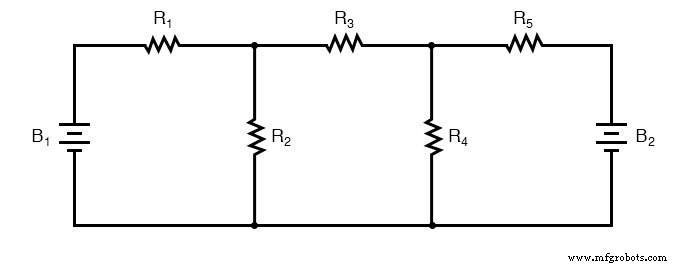
Um dieses Netzwerk mit Zweigströmen zu lösen, müssten wir fünf Variablen festlegen, um jeden einzelnen Strom in der Schaltung zu berücksichtigen (I1 bis I5 ). Dies würde fünf Gleichungen für die Lösung erfordern, in Form von zwei KCL-Gleichungen und drei KVL-Gleichungen (zwei Gleichungen für KCL an den Knoten und drei Gleichungen für KVL in jeder Schleife):
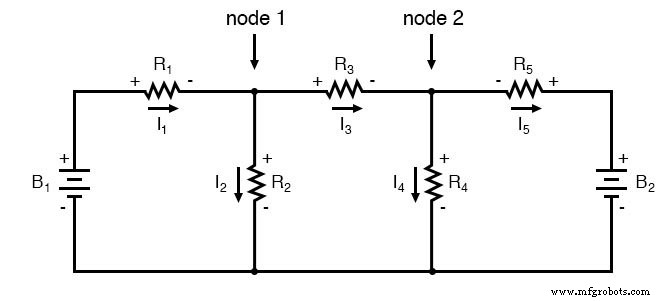
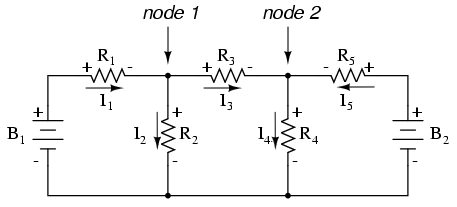

Ich nehme an, wenn Sie mit Ihrer Zeit nichts Besseres zu tun haben, als nach fünf unbekannten Variablen mit fünf Gleichungen aufzulösen, könnte es Ihnen nichts ausmachen, die Branch Current-Analysemethode für diese Schaltung zu verwenden. Für diejenigen von uns, die haben Bessere Dinge mit unserer Zeit zu tun, ist die Mesh Current-Methode viel einfacher und erfordert nur drei Unbekannte und drei Gleichungen zum Lösen:
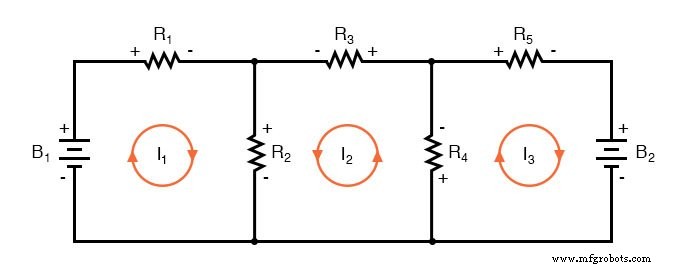
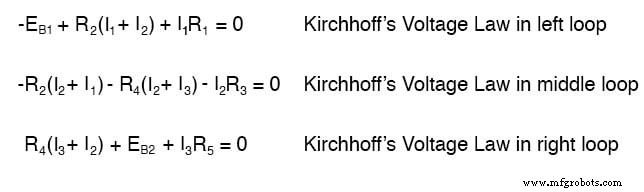
Weniger zu bearbeitende Gleichungen sind ein entscheidender Vorteil, insbesondere wenn eine gleichzeitige Gleichungslösung von Hand (ohne Taschenrechner) durchgeführt wird.
Unausgeglichene Wheatstone-Brücke
Eine andere Art von Schaltung, die sich gut für Mesh Current eignet, ist die unsymmetrische Wheatstone-Brücke. Nehmen Sie zum Beispiel diese Schaltung:
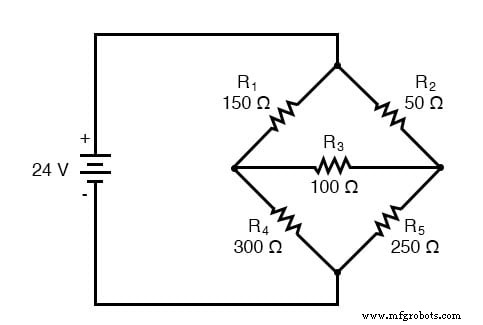
Da die Verhältnisse von R1 /R4 und R2 /R5 ungleich sind, wissen wir, dass die Spannung am Widerstand R3 . anliegt , und eine gewisse Menge an Strom durch. Wie zu Beginn dieses Kapitels besprochen, ist diese Art von Schaltung durch normale Serien-Parallel-Analyse irreduzibel und kann nur mit einer anderen Methode analysiert werden.
Wir könnten die Branch Current-Methode auf diese Schaltung anwenden, aber dafür wären sechs Ströme (I1 bis I6 ), was zu einem sehr großen Satz gleichzeitig zu lösender Gleichungen führt. Mit der Mesh Current-Methode können wir jedoch für alle Ströme und Spannungen mit viel weniger Variablen auflösen.
Netz zeichnen
Der erste Schritt bei der Mesh-Current-Methode besteht darin, gerade genug Mesh-Ströme zu ziehen, um alle Komponenten in der Schaltung zu berücksichtigen. Wenn man sich unsere Brückenschaltung ansieht, sollte es offensichtlich sein, wo zwei dieser Ströme platziert werden:
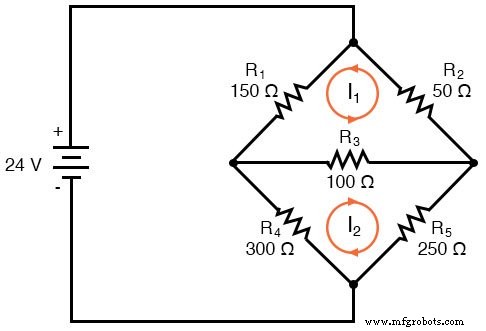
Die Richtungen dieser Maschenströme sind natürlich willkürlich. Zwei Maschenströme reichen in dieser Schaltung jedoch nicht aus, da weder I1 noch I2 geht durch die Batterie. Wir müssen also einen dritten Maschenstrom hinzufügen, I3 :
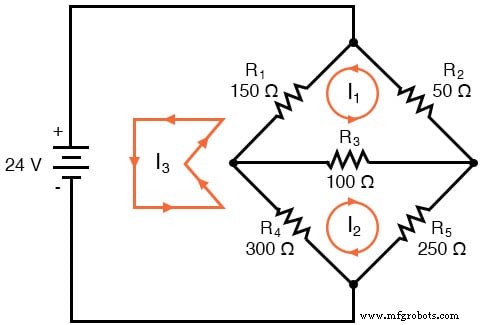
Hier habe ich I3 gewählt zum Loopen von der Unterseite des Akkus durch R4 , bis R1 , und zurück zur Oberseite des Akkus. Dies ist nicht der einzige Weg, den ich für I3 hätte wählen können , aber es scheint am einfachsten zu sein.
Beschriften Sie die Polaritäten des Spannungsabfalls des Widerstands
Jetzt müssen wir die Polaritäten des Spannungsabfalls des Widerstands beschriften, indem wir jeder der angenommenen Stromrichtungen folgen:
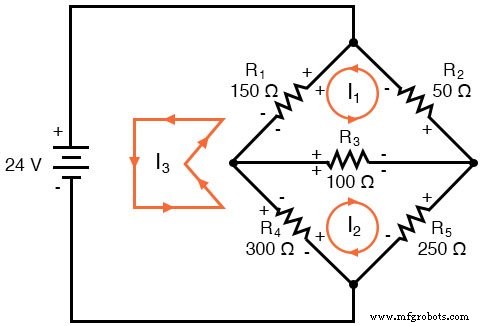
Beachten Sie hier etwas sehr Wichtiges:am Widerstand R4 stimmen die Polaritäten für die jeweiligen Maschenströme nicht überein. Dies liegt daran, dass diese Netzströme (I2 und ich3 ) durchlaufen R4 in verschiedene Richtungen. Dies schließt die Verwendung der Analysemethode Mesh Current nicht aus, verkompliziert sie jedoch ein wenig. Später werden wir jedoch zeigen, wie man den R4 . vermeidet aktuellen Zusammenstoß. (Siehe Beispiel unten)
KVL verwenden
Generieren einer KVL-Gleichung für die oberste Schleife der Brücke, ausgehend vom obersten Knoten und im Uhrzeigersinn verfolgend:

In dieser Gleichung repräsentieren wir die gemeinsamen Richtungen von Strömen durch ihre Summen durch gemeinsame Widerstände. Zum Beispiel Widerstand R3 , mit einem Wert von 100 Ω, hat seinen Spannungsabfall in der obigen KVL-Gleichung durch den Ausdruck 100(I1 + I2 ), da beide Ströme I1 und ich2 gehe durch R3 von rechts nach links. Das gleiche gilt für den Widerstand R1 , wobei der Spannungsabfallausdruck als 150(I1 + I3 ), da beide I1 und ich3 gehe von unten nach oben durch diesen Widerstand und arbeite so zusammen um seinen Spannungsabfall zu erzeugen.
Das Generieren einer KVL-Gleichung für die untere Schleife der Brücke wird nicht so einfach sein, da wir zwei Ströme haben, die durch den Widerstand R4 . gegeneinander laufen . So mache ich es (beginne am rechten Knoten und gehe gegen den Uhrzeigersinn):

Beachten Sie, dass der zweite Term in der ursprünglichen Form der Gleichung den Widerstand R4 . hat 's Wert von 300 Ω multipliziert mit der Differenz zwischen I2 und ich3 (I2 - I3 ). Auf diese Weise stellen wir den kombinierten Effekt zweier Maschenströme dar, die in entgegengesetzte Richtungen durch dieselbe Komponente fließen. Die Wahl der passenden mathematischen Zeichen ist hier sehr wichtig:300(I2 - I3 ) bedeutet nicht dasselbe wie 300(I3 - I2 ). Ich habe mich entschieden, 300 zu schreiben (I2 - I3 ) weil ich zuerst an I2 . dachte Wirkung (Erzeugung eines positiven Spannungsabfalls, Messung mit einem imaginären Voltmeter über R4 , rotes Blei unten und schwarzes Blei oben) und sekundär von I3 s-Effekt (erzeugt einen negativen Spannungsabfall, rotes Kabel unten und schwarzes Kabel oben). Wenn ich in Bezug auf I3 gedacht hätte Wirkung zuerst und I2 sekundär, wenn ich meine imaginären Voltmeter-Leitungen in den gleichen Positionen hielt (rot unten und schwarz oben), wäre der Ausdruck -300(I3 - I2 ). Beachten Sie, dass dieser Ausdruck ist mathematisch äquivalent zum ersten:+300(I2 - I3 ).
Nun, das kümmert sich um zwei Gleichungen, aber ich brauche noch eine dritte Gleichung, um meinen simultanen Gleichungssatz von drei Variablen, drei Gleichungen, zu vervollständigen. Diese dritte Gleichung muss auch die Spannung der Batterie beinhalten, die bis zu diesem Punkt in keiner der beiden vorherigen KVL-Gleichungen auftaucht. Um diese Gleichung zu generieren, zeichne ich mit meinem imaginären Voltmeter erneut eine Schleife, beginnend am unteren (negativen) Pol der Batterie, im Uhrzeigersinn (wiederum ist die Richtung, in die ich gehe, willkürlich und muss nicht mit der Richtung übereinstimmen.) des Maschenstroms in dieser Schleife):

Auflösung für die Ströme
Auflösen nach I1 , I2 , und ich3 mit der von uns bevorzugten simultanen Gleichungsmethode:

Beispiel: Verwenden Sie Octave, um die Lösung für I1 . zu finden , I2 , und ich3 aus der oben vereinfachten Form von Gleichungen.
Lösung: Geben Sie in Octave, einem Open-Source-Matlab®-Klon, die Koeffizienten in die A-Matrix zwischen eckigen Klammern mit durch Kommas getrennten Spaltenelementen und durch Semikolons getrennten Zeilen ein. Tragen Sie die Spannungen in den Spaltenvektor ein:b. Die unbekannten Ströme:I1 , 2 , und ich3 werden durch den Befehl berechnet:x=A\b. Diese sind im x-Spaltenvektor enthalten.
Der für I1 . ermittelte negative Wert sagt uns, dass die angenommene Richtung für diesen Maschenstrom falsch war. Somit sind die tatsächlichen Stromwerte durch jeden Widerstand wie folgt:
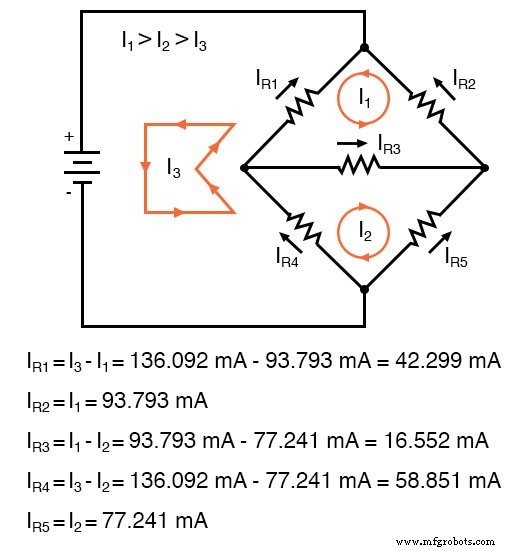
Berechnung der Spannungsabfälle an jedem Widerstand:
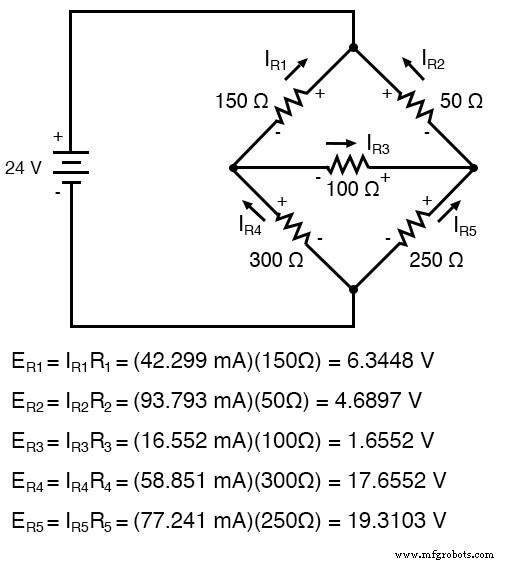
Eine SPICE-Simulation bestätigt die Genauigkeit unserer Spannungsberechnungen:
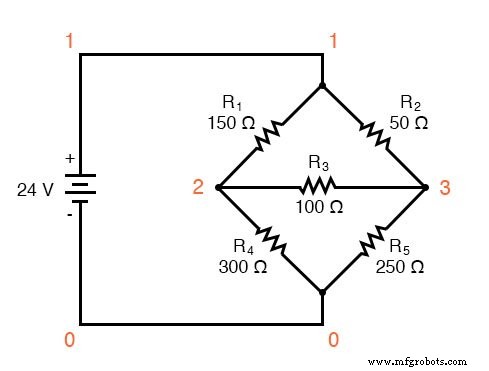
unsymmetrische Wheatstone-Brücke v1 1 0 r1 1 2 150 r2 1 3 50 r3 2 3 100 r4 2 0 300 r5 3 0 250 .dc v1 24 24 1 .print dc v(1,2) v(1,3) v(3,2) v(2,0) v(3,0) .Ende v1 v(1,2) v(1,3) v(3,2) v(2) v(3) 2.400E+01 6.345E+00 4.690E+00 1.655E+00 1.766E+01 1.931E+01
Beispiel:
(a) Finden Sie einen neuen Pfad für den Strom I3 das erzeugt bei keinem Widerstand eine widersprüchliche Polarität im Vergleich zu I1 oder I2 . R4 war die beleidigende Komponente. (b) Finden Sie Werte für I1 , I2 , und ich3 . (c) Finden Sie die fünf Widerstandsströme und vergleichen Sie sie mit den vorherigen Werten.
Lösung:
(a) Route I3 bis R5 , R3, und R1 wie abgebildet:
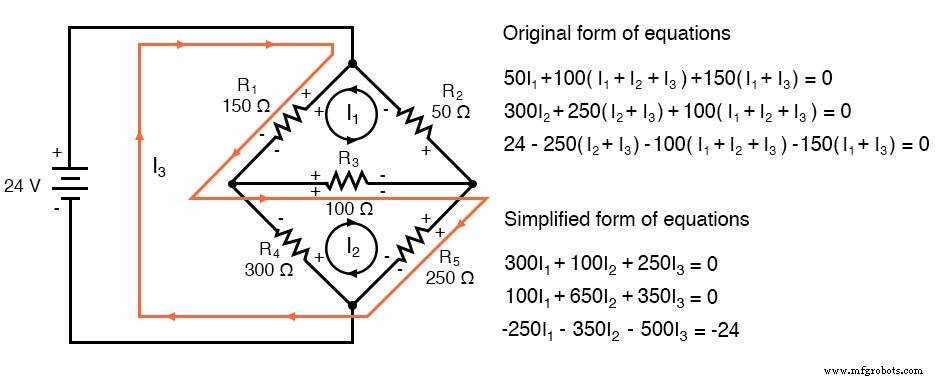
Beachten Sie, dass die widersprüchliche Polarität von R4 wurde entfernt. Darüber hinaus weist keiner der anderen Widerstände widersprüchliche Polaritäten auf.
(b) Octave, ein (kostenloser) Open-Source-Matlab-Klon, liefert einen Mesh-Stromvektor bei „x“:
Nicht alle Ströme I1 , I2 , und ich3 sind gleich (I2 ) wie die vorherige Brücke wegen unterschiedlicher Schleifenpfade Die Widerstandsströme sind jedoch mit den vorherigen Werten vergleichbar:
Da die Widerstandsströme mit den vorherigen Werten identisch sind, sind die Widerstandsspannungen identisch und müssen nicht erneut berechnet werden.
RÜCKBLICK:
- Zu befolgende Schritte für die Analysemethode "Mesh Current":
- (1) Ziehe Maschenströme in Schleifen des Stromkreises, genug, um alle Komponenten zu berücksichtigen.
- (2) Spannungsabfall-Polaritäten des Label-Widerstands basierend auf den angenommenen Richtungen der Maschenströme.
- (3) Schreiben Sie KVL-Gleichungen für jede Schleife der Schaltung, indem Sie das Produkt IR für E in jedem Widerstandsterm der Gleichung einsetzen. Wenn sich zwei Maschenströme durch eine Komponente schneiden, drücken Sie den Strom als die algebraische Summe dieser beiden Maschenströme aus (d. h. I1 + I2 ), wenn die Ströme durch diese Komponente in die gleiche Richtung fließen. Wenn nicht, drücken Sie den Strom ab der Differenz aus (d. h. I1 - I2 ).
- (4) Auflösen nach unbekannten Netzströmen (gleichzeitige Gleichungen).
- (5) Wenn eine Lösung negativ ist, ist die angenommene Stromrichtung falsch!
- (6) Fügen Sie algebraisch Maschenströme hinzu, um Stromkomponenten zu finden, die mehrere Maschenströme teilen.
- (7) Auflösen nach Spannungsabfällen an allen Widerständen (E=IR).
Netzstrom durch Inspektion
Wir werfen einen zweiten Blick auf die „Mesh-Current-Methode“, bei der alle Ströme im Uhrzeigersinn (cw) laufen. Die Motivation besteht darin, das Schreiben von Maschengleichungen zu vereinfachen, indem die Polarität des Spannungsabfalls des Widerstands ignoriert wird. Allerdings ist auf die Polarität der Spannungsquellen in Bezug auf die angenommene Stromrichtung zu achten. Das Vorzeichen der Spannungsabfälle am Widerstand folgt einem festen Muster.
Wenn wir einen Satz konventioneller Maschenstromgleichungen für die folgende Schaltung schreiben, wobei wir auf die Vorzeichen des Spannungsabfalls an den Widerständen achten, können wir die Koeffizienten in ein festes Muster umordnen:
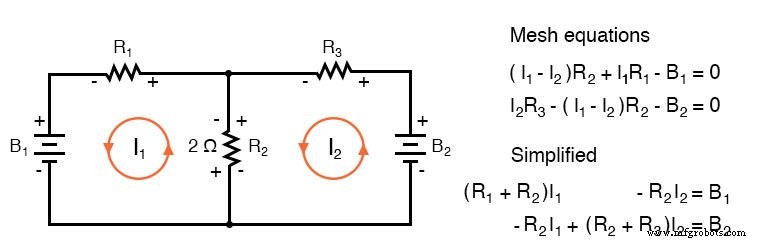
Einmal neu geordnet, können wir Gleichungen durch Inspektion schreiben. Die Vorzeichen der Koeffizienten folgen einem festen Muster im obigen Paar oder der Dreiergruppe in den folgenden Regeln.
Aktuelle Maschenregeln:
- Diese Methode geht von herkömmlichen Stromflussspannungsquellen aus. Ersetzen Sie jede Stromquelle parallel durch einen Widerstand durch eine äquivalente Spannungsquelle in Reihe mit einem äquivalenten Widerstand.
- Ignorieren Sie die Stromrichtung oder Spannungspolarität an den Widerständen und zeichnen Sie Stromschleifen gegen den Uhrzeigersinn, die alle Komponenten durchqueren. Verschachtelte Schleifen vermeiden.
- Schreiben Sie Spannungsgesetzgleichungen in Bezug auf unbekannte Ströme:I1 , I2 , und ich3 . Gleichung 1 Koeffizient 1, Gleichung 2, Koeffizient 2 und Gleichung 3 Koeffizient 3 sind die positiven Summen der Widerstände um die jeweiligen Schleifen herum.
- Alle anderen Koeffizienten sind negativ und repräsentieren den gemeinsamen Widerstand eines Schleifenpaares. Gleichung 1 Koeffizient 2 ist der gemeinsame Widerstand der Schleifen 1 und 2, Koeffizient 3 der gemeinsame Widerstand der Schleifen 1 und 3. Wiederholen Sie dies für andere Gleichungen und Koeffizienten.
- +(Summe der R-Schleife 1)I1 - (gemeinsame R-Schleife 1-2)I2 - (gemeinsame R-Schleife 1-3)I3 =E1
-(gemeinsame R-Schleife 1-2)I1 + ( Summe der R-Schleife 2)I2 - (gemeinsame R-Schleife 2-3)I3 =E2
-(gemeinsame R-Schleife 1-3)I1 - (gemeinsame R-Schleife 2-3)I2 + (Summe der R-Schleife 3 )I3 =E3 - Die rechte Seite der Gleichungen ist gleich einer Elektronenstrom-Flussspannungsquelle. Ein Spannungsanstieg in Bezug auf den angenommenen Strom gegen den Uhrzeigersinn ist positiv und 0 für keine Spannungsquelle.
- Löse Gleichungen für Netzströme:I1 , I2 , und I3. Mit KCL nach Strömen durch einzelne Widerstände auflösen. Lösen Sie nach Spannungen mit dem Ohmschen Gesetz und KVL auf.
Während die obigen Regeln für eine Schaltung mit drei Maschen spezifisch sind, können die Regeln auf kleinere oder größere Maschen ausgedehnt werden. Die folgende Abbildung veranschaulicht die Anwendung der Regeln. Die drei Ströme werden alle in die gleiche Richtung im Uhrzeigersinn gezogen. Für jede der drei Schleifen wird eine KVL-Gleichung geschrieben. Beachten Sie, dass die Widerstände nicht gepolt sind. Wir brauchen es nicht, um die Vorzeichen der Koeffizienten zu bestimmen. Allerdings müssen wir auf die Polarität der Spannungsquelle in Bezug auf die Stromrichtung achten. Die I3 Strom fließt im Uhrzeigersinn aus dem Pluspol (+) der 24-V-Quelle und kehrt dann zum (-)-Pol zurück. Dies ist ein Spannungsanstieg für den herkömmlichen Stromfluss. Daher ist die dritte Gleichung auf der rechten Seite -24V.
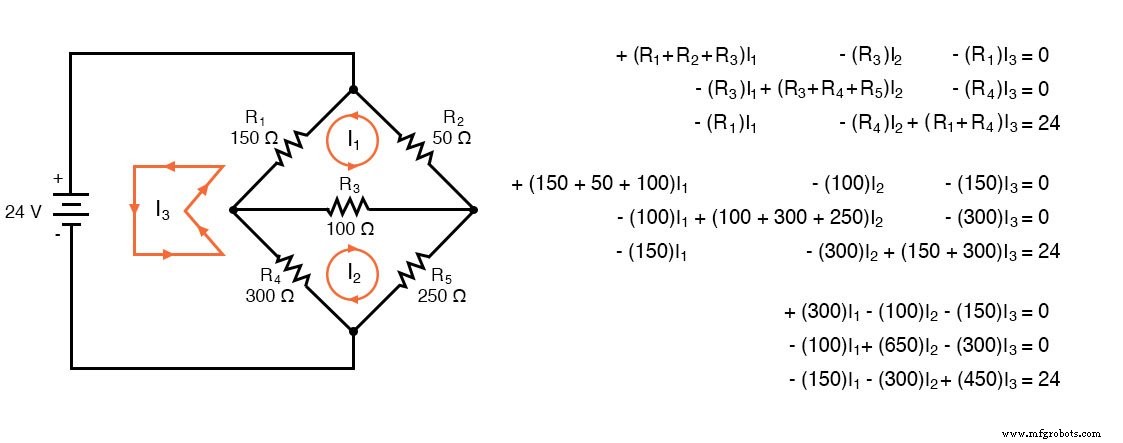
Geben Sie in Octave die Koeffizienten in die A-Matrix mit durch Kommas getrennten Spaltenelementen und durch Semikolon getrennten Zeilen ein. Tragen Sie die Spannungen in den Spaltenvektor ein b. Löse nach den unbekannten Strömen auf:I1 , I2 , und ich3 mit dem Befehl:x=A\b. Diese Ströme sind im x-Spaltenvektor enthalten. Die positiven Werte zeigen an, dass die drei Maschenströme alle im angenommenen Uhrzeigersinn fließen.
Die Maschenströme entsprechen der vorherigen Lösung durch ein anderes Maschenstromverfahren. Die Berechnung der Widerstandsspannungen und -ströme ist identisch mit der vorherigen Lösung. Keine Notwendigkeit, hier zu wiederholen.
Beachten Sie, dass elektrotechnische Texte auf konventionellem Stromfluss basieren. Die Loop-Current-Mesh-Current-Methode in diesen Texten lässt die angenommenen Mesh-Ströme im Uhrzeigersinn laufen . Der konventionelle Strom fließt aus dem (+)-Pol der Batterie durch den Stromkreis und kehrt zum (-)-Pol zurück. Ein konventioneller Strom-Spannungs-Anstieg entspricht der Verfolgung des angenommenen Stroms von (-) nach (+) durch beliebige Spannungsquellen.
Ein weiteres Beispiel einer vorherigen Schaltung folgt. Der Widerstand um Schleife 1 beträgt 6 , um Schleife 2:3 . Der gemeinsame Widerstand beider Schleifen beträgt 2 . Beachten Sie die Koeffizienten von I1 und ich2 im Gleichungspaar. Verfolgen des angenommenen Stroms von Schleife 1 im Uhrzeigersinn durch B1 von (+) nach (-) entspricht einem Anstieg der Elektronenstromflussspannung.
Somit ist das Vorzeichen der 28 V positiv. Die Schleife 2 im Gegenuhrzeigersinn nahm Stromspuren (-) bis (+) durch B2 . an , ein Spannungsabfall. Somit ist das Vorzeichen von B2 negativ ist, -7 in der zweiten Maschengleichung. Auch hier gibt es keine Polaritätsmarkierungen an den Widerständen. Sie fließen auch nicht in die Gleichungen ein.
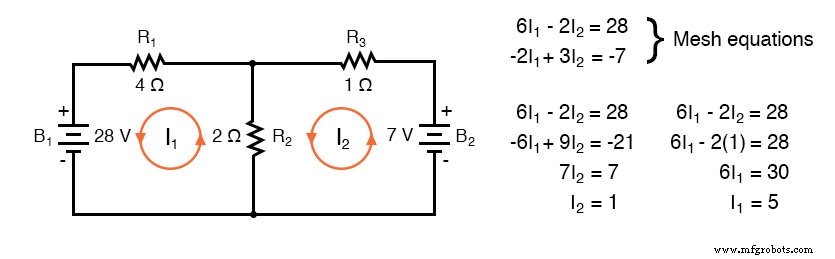
Die Ströme I1 =5 A und I2 =1 A sind beide positiv. Beide fließen in Richtung der Schleifen im Uhrzeigersinn. Dies vergleicht sich mit früheren Ergebnissen.
Zusammenfassung:
- Die modifizierte Maschenstrommethode vermeidet die Vorzeichenbestimmung der Gleichungskoeffizienten, indem alle Maschenströme für den herkömmlichen Stromfluss im Uhrzeigersinn gezeichnet werden.
- Wir müssen jedoch das Vorzeichen aller Spannungsquellen in der Schleife bestimmen. Die Spannungsquelle ist positiv, wenn der angenommene ccw-Strom mit der Batterie (Quelle) fließt. Das Vorzeichen ist negativ, wenn der angenommene ccw-Strom gegen die Batterie fließt.
- Weitere Informationen finden Sie in den obigen Regeln.
VERWANDTES ARBEITSBLATT:
- Arbeitsblatt zur DC-Netzstromanalyse
Industrietechnik
- Lösen simultaner Gleichungen:Die Substitutionsmethode und die Additionsmethode
- Beispielschaltungen und Netzlisten
- Einführung in Dioden und Gleichrichter
- Spannung und Strom
- Spannungs- und Stromberechnungen
- Was ist Netzanalyse:Verfahren und seine Beispiele
- Abstrakte C#-Klasse und -Methode
- C# Teilklasse und Teilmethode
- Versiegelte C#-Klasse und -Methode
- Strom, Leistung und Drehmoment in drehzahlgeregelten Antrieben



