Knotenspannungsmethode
Die Knotenspannungsanalysemethode löst unbekannte Spannungen an Schaltungsknoten im Sinne eines Systems von KCL-Gleichungen auf. Diese Analyse sieht seltsam aus, da sie den Austausch von Spannungsquellen durch gleichwertige Stromquellen beinhaltet. Außerdem werden Widerstandswerte in Ohm durch äquivalente Leitwerte in Siemens ersetzt, G =1/R. Siemens (S) ist die Einheit des Leitwerts und hat die Einheit mho ersetzt. Auf jeden Fall S =Ω-1. Und S =mho (veraltet).
Methode zur Berechnung der Knotenspannung
Wir beginnen mit einer Schaltung mit herkömmlichen Spannungsquellen. Ein gemeinsamer Knoten E0 wird als Bezugspunkt gewählt. Die Knotenspannungen E1 und E2 werden in Bezug auf diesen Punkt berechnet.
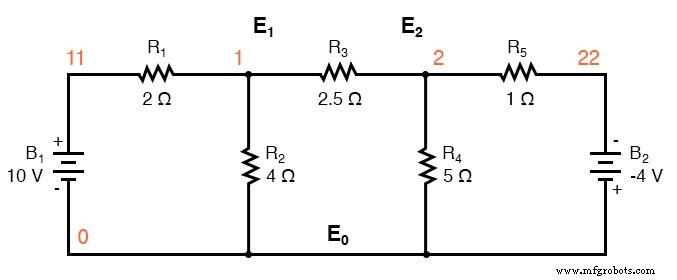
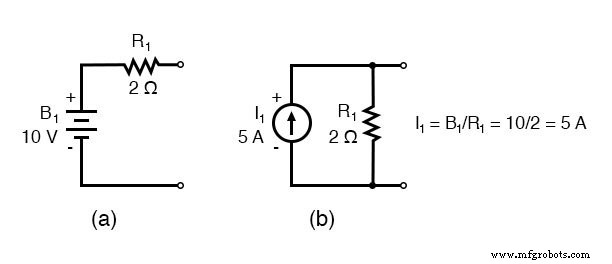
Das Ersetzen von Spannungsquellen und zugehörigen Serienwiderständen durch äquivalente Stromquellen und Parallelwiderstände ergibt die modifizierte Schaltung. Ersetzen Sie den Widerstand in Ohm durch die Widerstandsleitwerte in Siemens.
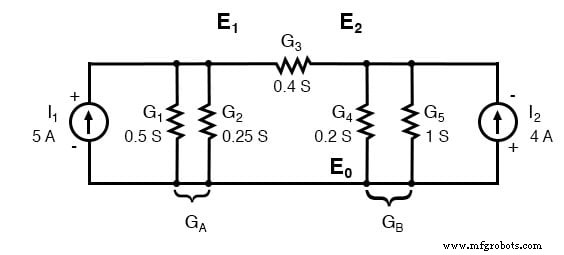
Die parallelen Leitwerte (Widerstände) können durch Addition der Leitwerte kombiniert werden. Wir werden die Schaltung jedoch nicht neu zeichnen. Die Schaltung ist bereit für die Anwendung der Knotenspannungsmethode.
Um eine allgemeine Knotenspannungsmethode abzuleiten, schreiben wir ein Paar von KCL-Gleichungen in Bezug auf unbekannte Knotenspannungen V1 und V2 dieses eine Mal. Wir tun dies, um ein Muster zum Schreiben von Gleichungen durch Inspektion zu veranschaulichen.
Die Koeffizienten des letzten Gleichungspaares oben wurden neu angeordnet, um ein Muster zu zeigen. Die Summe der mit dem ersten Knoten verbundenen Leitwerte ist der positive Koeffizient der ersten Spannung in Gleichung (1). Die Summe der mit dem zweiten Knoten verbundenen Leitwerte ist der positive Koeffizient der zweiten Spannung in Gleichung (2). Die anderen Koeffizienten sind negativ und repräsentieren Konduktanzen zwischen den Knoten. Bei beiden Gleichungen ist die rechte Seite gleich der jeweiligen Stromquelle, die mit dem Knoten verbunden ist. Dieses Muster ermöglicht es uns, die Gleichungen durch Inspektion schnell zu schreiben. Dies führt zu einem Regelwerk für die Knotenspannungsanalysemethode.
Knotenspannungsregeln:
- Wandeln Sie Spannungsquellen in Reihe mit einem Widerstand in eine äquivalente Stromquelle mit parallelem Widerstand um.
- Ändern Sie die Widerstandswerte in Leitwerte.
- Wählen Sie einen Referenzknoten aus (E0 )
- Unbekannte Spannungen zuweisen (E1 )(E2 ) ... (EN )zu den restlichen Knoten.
- Schreiben Sie eine KCL-Gleichung für jeden Knoten 1,2, ... N. Der positive Koeffizient der ersten Spannung in der ersten Gleichung ist die Summe der mit dem Knoten verbundenen Leitwerte. Der Koeffizient für die zweite Spannung in der zweiten Gleichung ist die Summe der mit diesem Knoten verbundenen Leitwerte. Wiederholen Sie dies für den Koeffizienten der dritten Spannung, die dritte Gleichung und andere Gleichungen. Diese Koeffizienten fallen auf eine Diagonale.
- Alle anderen Koeffizienten für alle Gleichungen sind negativ und repräsentieren Konduktanzen zwischen Knoten. Die erste Gleichung, der zweite Koeffizient ist der Leitwert von Knoten 1 zu Knoten 2, der dritte Koeffizient ist der Leitwert von Knoten 1 zu Knoten 3. Tragen Sie negative Koeffizienten für andere Gleichungen ein.
- Die rechte Seite der Gleichungen ist die Stromquelle, die mit den jeweiligen Knoten verbunden ist.
- Löse das Gleichungssystem für unbekannte Knotenspannungen.
Beispiel einer Knotenspannungsmethode
Beispiel: Stellen Sie die Gleichungen auf und lösen Sie die Knotenspannungen mit den Zahlenwerten in der obigen Abbildung auf.
Lösung:
Die Lösung zweier Gleichungen kann mit einem Taschenrechner oder mit einer Oktave (nicht gezeigt) durchgeführt werden. Die Lösung wird mit SPICE anhand des ursprünglichen Schaltplans mit Spannungsquellen verifiziert. Die Schaltung mit den Stromquellen hätte jedoch simuliert werden können.
Noch ein Beispiel. Dieser hat drei Knoten. Die Leitwerte sind im Schaltplan nicht aufgeführt. G1 . jedoch =1/R1 , usw.
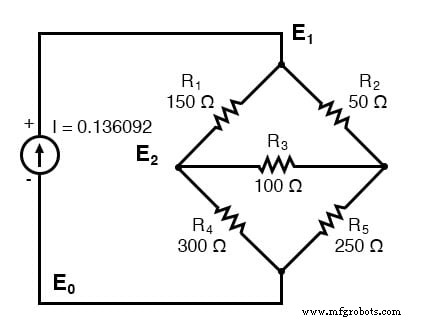
Es gibt drei Knoten zum Schreiben von Gleichungen durch Inspektion. Beachten Sie, dass die Koeffizienten für Gleichung (1) positiv sind E1 , Gleichung (2) E2 , und Gleichung (3) E3 . Dies sind die Summen aller Leitwerte, die mit den Knoten verbunden sind. Alle anderen Koeffizienten sind negativ und repräsentieren eine Leitfähigkeit zwischen Knoten. Die rechte Seite der Gleichungen ist die zugehörige Stromquelle, 0,136092 A für die einzige Stromquelle am Knoten 1. Die anderen Gleichungen auf der rechten Seite sind wegen fehlender Stromquellen null. Wir sind zu faul, die Leitwerte für die Widerstände im Diagramm zu berechnen. Somit sind die tiefgestellten Gs die Koeffizienten.
Wir sind so faul, dass wir reziproke Widerstände und Summen reziproker Widerstände in die Oktav-„A“-Matrix eingeben und Oktave die Leitwertmatrix nach „A=“ berechnen lassen. Die anfängliche Eingabezeile war so lang, dass sie in drei Reihen aufgeteilt wurde. Dies unterscheidet sich von früheren Beispielen. Die eingegebene Matrix „A“ wird durch eckige Klammern am Anfang und am Ende abgegrenzt. Spaltenelemente sind durch Leerzeichen getrennt. Zeilen werden durch „neue Zeile“ getrennt. Kommas und Semikolons werden als Trennzeichen nicht benötigt. Der Stromvektor bei „b“ ist jedoch durch Semikolon getrennt, um einen Spaltenvektor von Strömen zu erhalten.
Beachten Sie, dass die Diagonalkoeffizienten der Matrix „A“ positiv sind, dass alle anderen Koeffizienten negativ sind.
Die Lösung als Spannungsvektor liegt bei „x“. E1 =24.000 V, E2 =17,655 V, E3 =19,310 V. Diese drei Spannungen sind vergleichbar mit den bisherigen Maschenstrom- und SPICE-Lösungen für das Problem der unsymmetrischen Brücke. Dies ist kein Zufall, denn die Stromquelle von 0,13609 A wurde bewusst gewählt, um die bei diesem Problem als Spannungsquelle verwendeten 24 V zu liefern.
Zusammenfassung
- Angesichts eines Netzwerks von Leitwerten und Stromquellen löst die Knotenspannungsmethode der Schaltungsanalyse unbekannte Knotenspannungen aus KCL-Gleichungen auf.
- Siehe die Regeln oben für Details zum Schreiben der Gleichungen durch Inspektion.
- Die Einheit des Leitwerts G ist Siemens S. Der Leitwert ist der Kehrwert des Widerstands:G =1/R
VERWANDTE ARBEITSBLÄTTER:
- Arbeitsblatt für präzise Diodenschaltungen
- Arbeitsblatt Kirchhoffsche Gesetze
Industrietechnik



