Δ-Y- und Y-Δ-Conversions

In vielen Schaltungsanwendungen begegnen wir Komponenten, die auf eine von zwei Arten miteinander verbunden sind, um ein Netzwerk mit drei Anschlüssen zu bilden:die „Delta“- oder Δ-Konfiguration (auch bekannt als „Pi“ oder π) und die „Y“-Konfiguration ( auch bekannt als „T“) Konfiguration.

Es ist möglich, die richtigen Werte von Widerständen zu berechnen, die erforderlich sind, um eine Art von Netzwerk (Δ oder Y) zu bilden, das sich identisch verhält wie die andere Art, wie allein anhand der Anschlussverbindungen analysiert. Das heißt, wenn wir zwei separate Widerstandsnetzwerke hätten, ein und ein Y, jedes mit seinen nicht sichtbaren Widerständen und nur den drei Anschlüssen (A, B und C), die zum Testen freigelegt sind, könnten die Widerstände für die Größe von bemessen werden zwei Netze, so dass es keine Möglichkeit gäbe, ein Netz elektrisch vom anderen zu unterscheiden. Mit anderen Worten, äquivalente Δ- und Y-Netzwerke verhalten sich identisch.

Δ und Y-Umrechnungsgleichungen

Es gibt mehrere Gleichungen, die verwendet werden, um ein Netzwerk in das andere umzuwandeln:

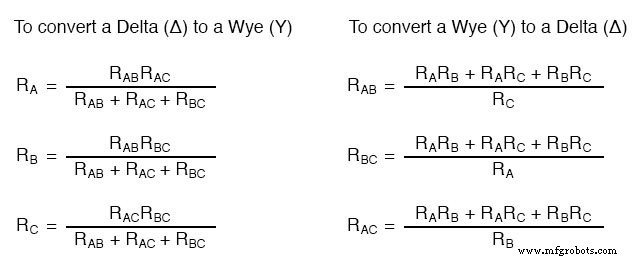
Δ- und Y-Netze werden häufig in 3-Phasen-Wechselstromnetzen gesehen (ein Thema, das in Band II dieser Buchreihe behandelt wird), aber selbst dann sind es normalerweise symmetrische Netze (alle Widerstände haben den gleichen Wert) und Umwandlung von einem in den anderen müssen keine so komplexen Berechnungen beinhalten. Wann müsste der durchschnittliche Techniker diese Gleichungen jemals verwenden?

Anwendung der Δ- und Y-Umwandlung

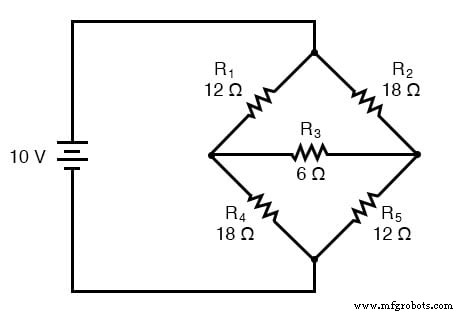
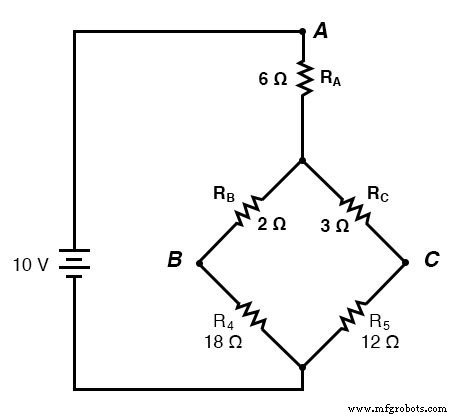
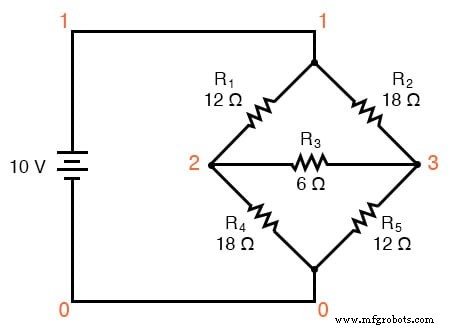
Eine Hauptanwendung für die Δ-Y-Wandlung ist die Lösung von unsymmetrischen Brückenschaltungen, wie der folgenden:

Die Lösung dieser Schaltung mit Branch Current- oder Mesh-Current-Analyse ist ziemlich kompliziert, und weder der Millman- noch der Superpositionssatz helfen, da es nur eine Stromquelle gibt. Wir könnten Thevenins oder Nortons Theorem verwenden, um R₃ . zu behandeln wie unsere Ladung, aber was wäre das für ein Spaß?

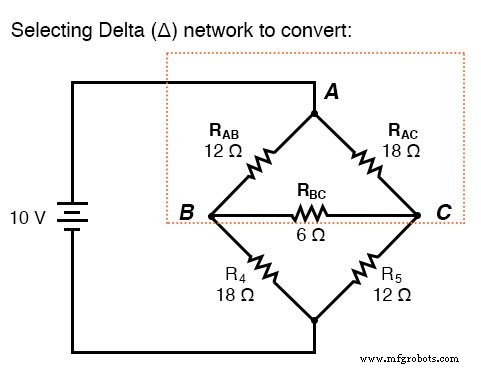
Wenn wir Widerstände R₁ . behandeln würden , R₂ , und R₃ als verbunden in einer Δ-Konfiguration (R_ab , R_ac , und R_bc ) und erzeugen ein äquivalentes Y-Netzwerk, um sie zu ersetzen, könnten wir diese Brückenschaltung in eine (einfache) Reihen-/Parallel-Kombinationsschaltung umwandeln:

Nach der Δ-Y-Umwandlung . . .

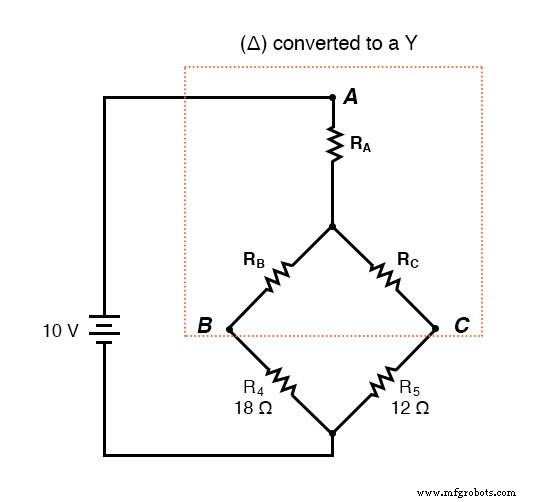
Wenn wir unsere Berechnungen korrekt durchführen, sind die Spannungen zwischen den Punkten A, B und C in der umgewandelten Schaltung die gleichen wie in der ursprünglichen Schaltung, und wir können diese Werte zurück in die ursprüngliche Brückenkonfiguration übertragen.

Widerstände R₄ und R₅ , bleiben natürlich bei 18 bzw. 12 gleich. Analysiert man nun die Schaltung als Reihen-/Parallelkombination, kommen wir zu folgenden Zahlen:

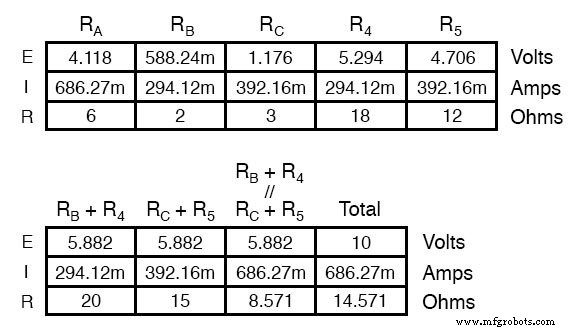
Wir müssen die Spannungsabfälle aus der obigen Tabelle verwenden, um die Spannungen zwischen den Punkten A, B und C zu bestimmen und zu sehen, wie sie sich addieren (oder subtrahieren, wie es bei der Spannung zwischen den Punkten B und C der Fall ist):

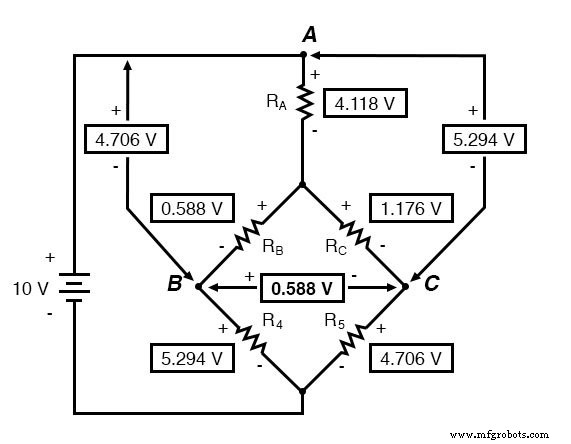
Jetzt, da wir diese Spannungen kennen, können wir sie auf die gleichen Punkte A, B und C in der ursprünglichen Brückenschaltung übertragen:

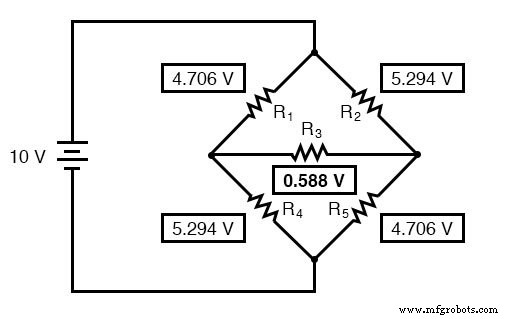
Spannungsabfälle an R₄ und R₅ , sind natürlich genau die gleichen wie in der Wandlerschaltung.

An dieser Stelle könnten wir diese Spannungen nehmen und Widerstandsströme durch die wiederholte Anwendung des Ohmschen Gesetzes (I=E/R) bestimmen:

Simulation mit SPICE

Eine kurze Simulation mit SPICE soll unsere Arbeit verifizieren:

unsymmetrische Brückenschaltung v1 1 0 r1 1 2 12 r2 1 3 18 r3 2 3 6 r4 2 0 18 r5 3 0 12 .dc v1 10 10 1 .print dc v(1,2) v(1,3) v(2,3) v(2,0) v(3,0) .Ende v1 v(1,2) v(1,3) v(2,3) v(2) v(3) 1.000E+01 4.706E+00 5.294E+00 5.882E-01 5.294E+00 4.706E+00 

Die Spannungswerte, von links nach rechts gelesen, stellen Spannungsabfälle an den fünf entsprechenden Widerständen dar, R₁ bis R₅ . Ich hätte auch Ströme zeigen können, aber da dies das Einfügen von „Dummy“-Spannungsquellen in die SPICE-Netzliste erfordert hätte und wir in erster Linie daran interessiert sind, die Δ-Y-Umwandlungsgleichungen und nicht das Ohmsche Gesetz zu validieren, reicht dies.

RÜCKBLICK:

• „Delta“ (Δ)-Netzwerke werden auch als „Pi“ (π)-Netzwerke bezeichnet.
• „Y“-Netzwerke werden auch als „T“-Netzwerke bezeichnet.
• Δ- und Y-Netzwerke können mit den richtigen Widerstandsgleichungen in ihre entsprechenden Gegenstücke umgewandelt werden. Mit „äquivalent“ meine ich, dass die beiden Netzwerke elektrisch identisch sind, gemessen von den drei Anschlüssen (A, B und C).
• Eine Brückenschaltung kann zu einer Reihen-/Parallelschaltung vereinfacht werden, indem die Hälfte von einem Δ- in ein Y-Netzwerk umgewandelt wird. Nachdem Spannungsabfälle zwischen den ursprünglichen drei Verbindungspunkten (A, B und C) gelöst wurden, können diese Spannungen über dieselben äquivalenten Punkte zurück auf die ursprüngliche Brückenschaltung übertragen werden.

VERWANDTES ARBEITSBLATT:

• Arbeitsblatt für Delta- und Wye-Dreiphasenschaltungen