Einführung in komplexe Zahlen

Wenn ich die Entfernung zwischen zwei Städten beschreiben müsste, könnte ich eine Antwort geben, die aus einer einzelnen Zahl in Meilen, Kilometern oder einer anderen linearen Maßeinheit besteht.

Wenn ich jedoch beschreiben sollte, wie man von einer Stadt in eine andere reist, müsste ich mehr Informationen liefern als nur die Entfernung zwischen diesen beiden Städten; Ich müsste auch Angaben zur Anfahrt machen auch zu reisen.

Die Art von Information, die eine einzelne Dimension ausdrückt, wie z. B. die lineare Entfernung, wird als Skalar bezeichnet Quantität in der Mathematik. Skalare Zahlen sind die Art von Zahlen, die Sie bisher in den meisten Ihrer mathematischen Anwendungen verwendet haben.

Die von einer Batterie erzeugte Spannung ist beispielsweise eine skalare Größe. Ebenso der Widerstand eines Drahtstücks (Ohm) oder der Strom durch es (Ampere).

Wenn wir jedoch beginnen, Wechselstromkreise zu analysieren, finden wir diese Menge an Spannung, Strom und sogar Widerstand (genannt Impedanz in Wechselstrom) sind nicht die bekannten eindimensionalen Größen, die wir gewohnt sind, in Gleichstromkreisen zu messen.

Vielmehr besitzen diese Größen, da sie dynamisch sind (in Richtung und Amplitude wechselnd), andere Dimensionen, die berücksichtigt werden müssen. Frequenz- und Phasenverschiebung sind zwei dieser Dimensionen, die ins Spiel kommen.

Selbst bei relativ einfachen Wechselstromkreisen, bei denen es sich nur um eine einzige Frequenz handelt, haben wir neben der Amplitude noch die Dimension der Phasenverschiebung zu bewältigen.

Um Wechselstromkreise erfolgreich zu analysieren, müssen wir mit mathematischen Objekten und Techniken arbeiten, die diese mehrdimensionalen Größen darstellen können.

Hier müssen wir skalare Zahlen für etwas besser geeignetes aufgeben:komplexe Zahlen . Genau wie im Beispiel der Wegbeschreibung von einer Stadt zur anderen weisen Wechselstromgrößen in einer Einfrequenzschaltung sowohl eine Amplituden- (Analogie:Entfernung) als auch eine Phasenverschiebung (Analogie:Richtung) auf.

Eine komplexe Zahl ist eine einzelne mathematische Größe, die diese beiden Dimensionen der Amplituden- und Phasenverschiebung gleichzeitig ausdrücken kann.

Grafische Darstellung komplexer Zahlen

Komplexe Zahlen sind leichter zu verstehen, wenn sie grafisch dargestellt werden. Wenn ich eine Linie mit einer bestimmten Länge (Größe) und einem bestimmten Winkel (Richtung) zeichne, habe ich eine grafische Darstellung einer komplexen Zahl, die in der Physik allgemein als Vektor bekannt ist :(Abbildung unten)

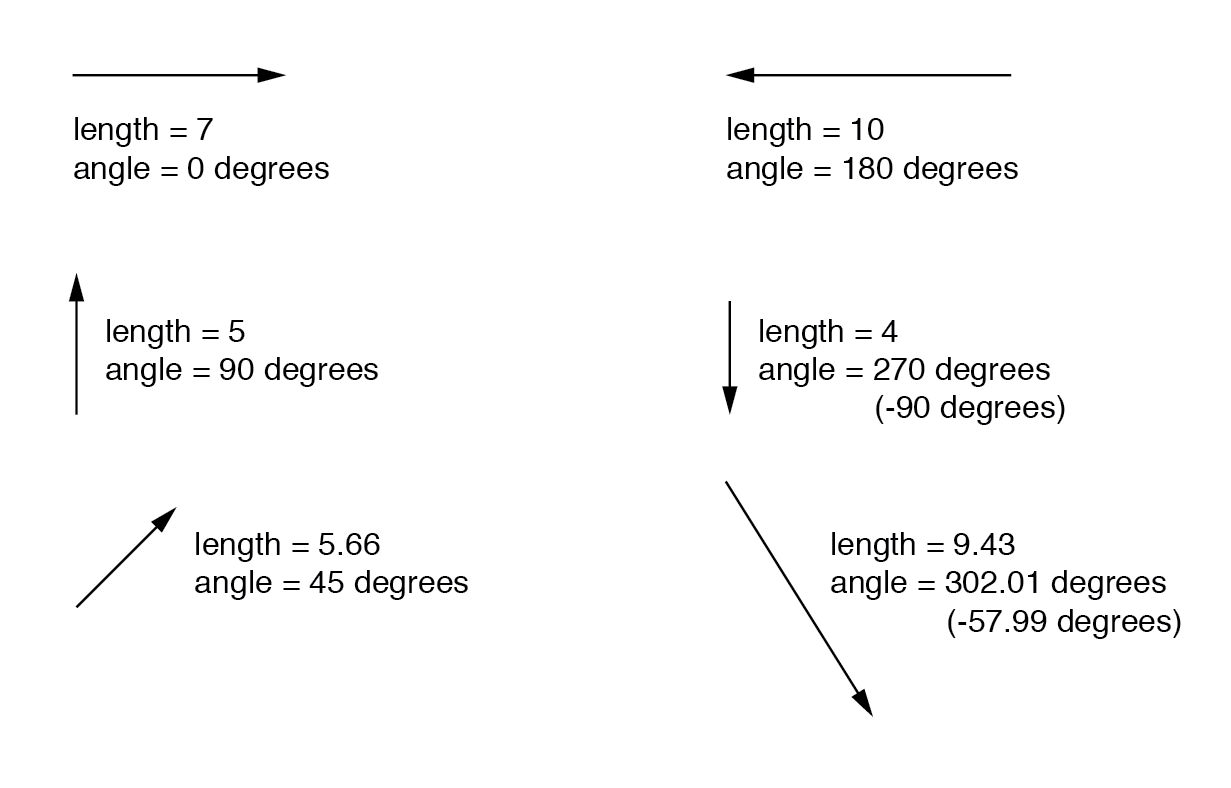
Wie Entfernungen und Richtungen auf einer Karte muss es einen gemeinsamen Bezugsrahmen geben, damit Winkelangaben eine Bedeutung haben. In diesem Fall wird direkt rechts als 0 ^o . angesehen , und Winkel werden in positiver Richtung gegen den Uhrzeigersinn gezählt:(Abbildung unten)

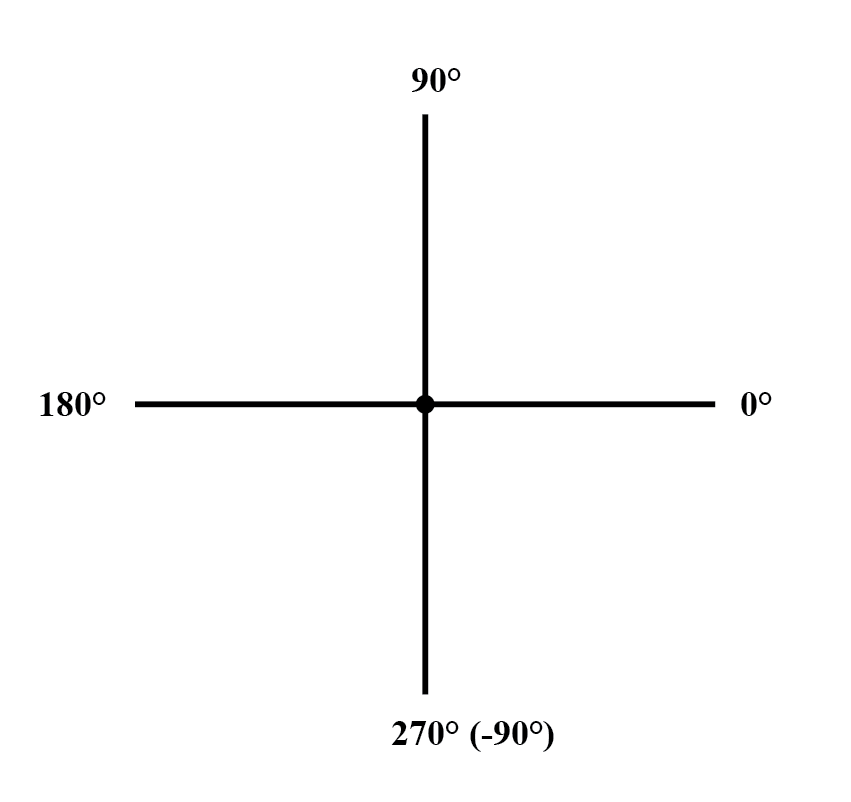
Die Idee, eine Zahl grafisch darzustellen, ist nichts Neues. Das haben wir alle in der Grundschule mit dem „Zahlenstrahl“ gelernt:(Abbildung unten)

Wir haben sogar gelernt, wie Addition und Subtraktion funktionieren, indem wir gesehen haben, wie sich Längen (Größen) stapeln, um eine endgültige Antwort zu geben:(Abbildung unten)

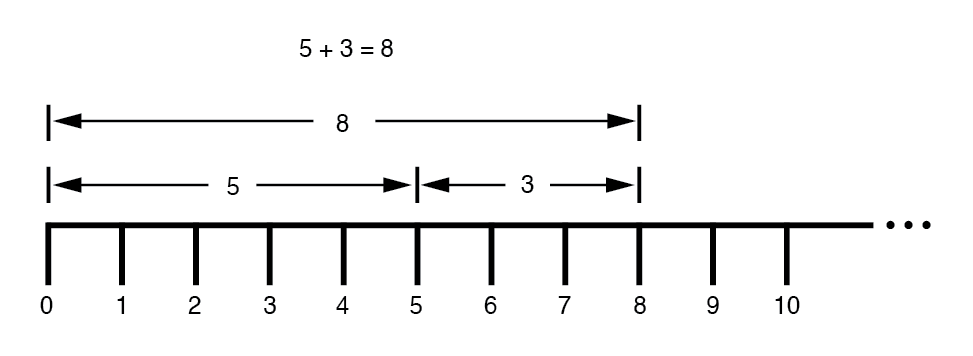
Später haben wir erfahren, dass es Möglichkeiten gibt, die Werte zwischen zu bestimmen die ganzen Zahlen auf der Linie markiert. Dies waren Bruch- oder Dezimalzahlen:(Abbildung unten)

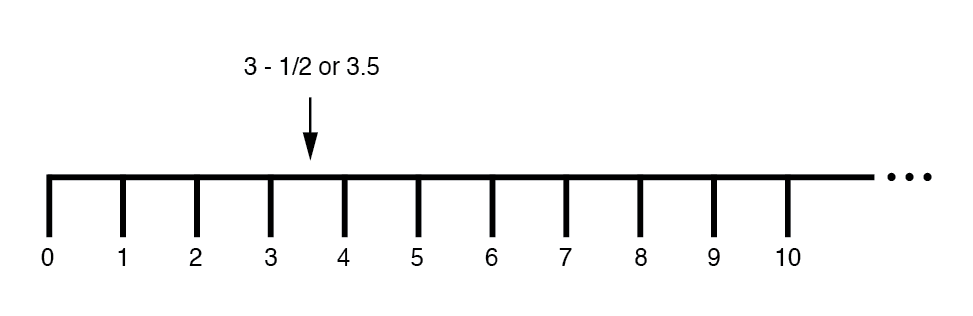
Diese in der Grundschule gelernten Zahlenfelder (ganze, ganze, rationale, irrationale, reelle usw.) haben eines gemeinsam:Sie sind alle eindimensional . Die Geradlinigkeit des Zahlenstrahls verdeutlicht dies grafisch.

Sie können sich auf der Zahlenlinie nach oben oder unten bewegen, aber alle „Bewegungen“ entlang dieser Linie sind auf eine einzige Achse (horizontal) beschränkt.

Eindimensionale Skalarzahlen sind vollkommen ausreichend, um Perlen zu zählen, das Gewicht darzustellen oder die DC-Batteriespannung zu messen, aber sie sind nicht in der Lage, etwas Komplexeres wie die Entfernung und . darzustellen Richtung zwischen zwei Städten, oder die Amplitude und Phase einer AC-Wellenform.

Um solche Größen darzustellen, benötigen wir mehrdimensionale Darstellungen. Mit anderen Worten, wir brauchen einen Zahlenstrahl, der in verschiedene Richtungen zeigen kann, und genau das ist ein Vektor.

RÜCKBLICK:

• Ein Skalar Zahl ist die Art von mathematischen Objekten, an die der Mensch im Alltag gewöhnt ist:eine eindimensionale Größe wie Temperatur, Länge, Gewicht usw.
• Eine komplexe Zahl ist eine mathematische Größe, die zwei Dimensionen von Größe und Richtung repräsentiert.
• Ein Vektor ist eine grafische Darstellung einer komplexen Zahl. Es sieht aus wie ein Pfeil mit einem Startpunkt, einer Spitze, einer bestimmten Länge und einer bestimmten Richtung. Manchmal das Wort phasor wird in elektrischen Anwendungen verwendet, bei denen der Winkel des Vektors die Phasenverschiebung zwischen den Wellenformen darstellt.

VERWANDTES ARBEITSBLATT:

• AC-Phase Arbeitsblatt