Parallel-Widerstands-Induktor-Schaltungen

Nehmen wir die gleichen Komponenten für unsere Serien-Beispielschaltung und schalten sie parallel:

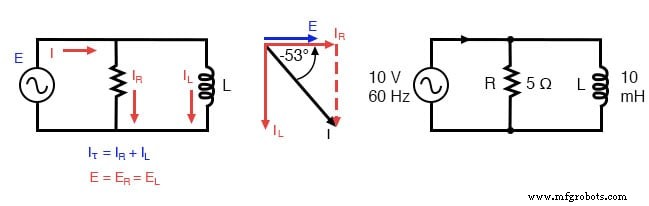
Parallel R-L-Schaltung.

Da die Stromquelle dieselbe Frequenz wie die beispielhafte Reihenschaltung hat und sowohl der Widerstand als auch die Induktivität dieselben Widerstands- bzw. Induktivitätswerte aufweisen, müssen sie auch dieselben Impedanzwerte aufweisen. So können wir unsere Analysetabelle mit denselben „gegebenen“ Werten beginnen:

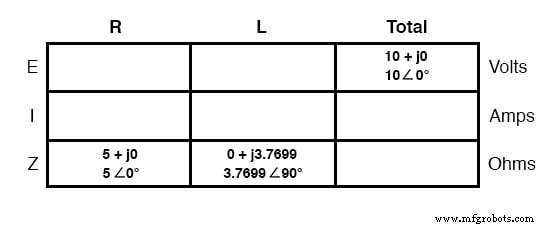
Der einzige Unterschied in unserer Analysetechnik besteht diesmal darin, dass wir die Regeln für Parallelschaltungen anstelle der Regeln für Reihenschaltungen anwenden. Der Ansatz ist grundsätzlich der gleiche wie bei DC. Wir wissen, dass die Spannung von allen Komponenten in einer Parallelschaltung gleichmäßig geteilt wird, daher können wir die Gesamtspannung (10 Volt ∠ 0°) auf alle Komponentenspalten übertragen:

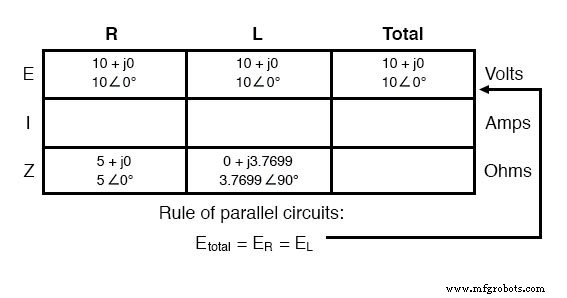
Jetzt können wir das Ohmsche Gesetz (I=E/Z) vertikal auf zwei Spalten der Tabelle anwenden und den Strom durch den Widerstand und den Strom durch die Induktivität berechnen:

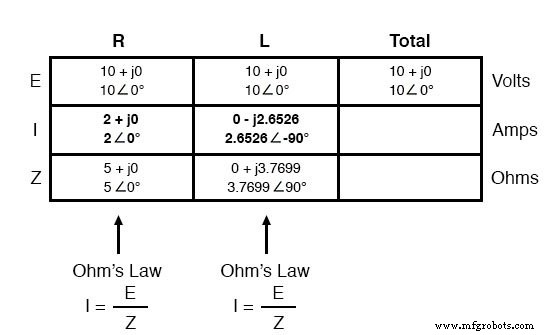
Wie bei Gleichstromkreisen addieren sich Zweigströme in einem parallelen Wechselstromkreis zum Gesamtstrom (das Kirchhoffsche Stromgesetz gilt für Wechselstrom immer noch wie für Gleichstrom):

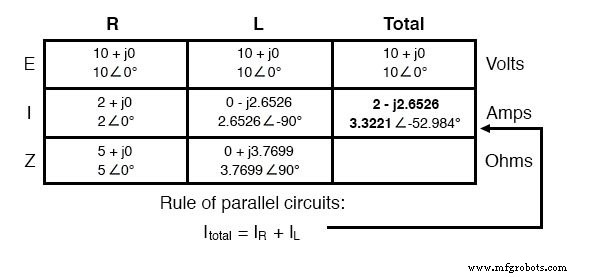
Schließlich kann die Gesamtimpedanz mithilfe des Ohmschen Gesetzes (Z=E/I) vertikal in der Spalte „Gesamt“ berechnet werden. Übrigens kann die Parallelimpedanz auch berechnet werden, indem eine reziproke Formel verwendet wird, die mit der identisch ist, die bei der Berechnung der Parallelwiderstände verwendet wird.

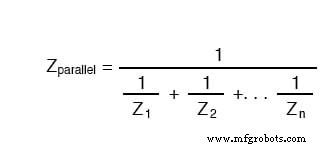
Das einzige Problem bei der Verwendung dieser Formel besteht darin, dass sie normalerweise viele Taschenrechnertastenanschläge erfordert.

Und wenn Sie entschlossen sind, eine Formel wie diese „Langhand“ durchzuspielen, seien Sie auf sehr viel Arbeit vorbereitet! Aber wie bei Gleichstromkreisen haben wir oft mehrere Möglichkeiten, die Größen in unseren Analysetabellen zu berechnen, und dieses Beispiel ist nicht anders.

Egal, wie Sie die Gesamtimpedanz berechnen (Ohmsches Gesetz oder die Kehrwertformel), Sie erhalten denselben Wert:

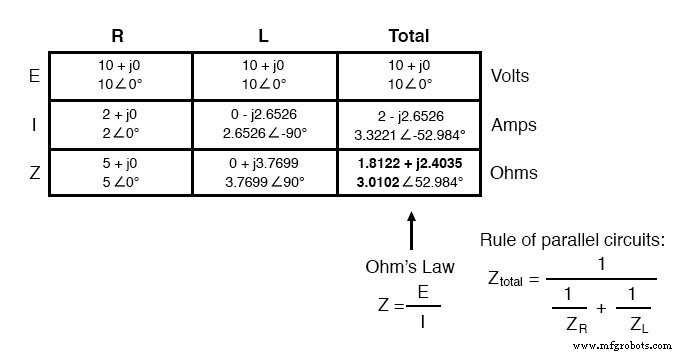
RÜCKBLICK:

• Impedanzen (Z) werden wie Widerstände (R) bei der Parallelschaltungsanalyse verwaltet:Parallelimpedanzen verkleinern sich mit der Kehrwertformel zur Gesamtimpedanz. Führen Sie nur alle Berechnungen in komplexer (nicht skalarer) Form durch! ZGesamt =1/(1/Z1 + 1/Z2 + . . . 1/Zn)
• Ohmsches Gesetz für Wechselstromkreise:E =IZ; ich =E/Z; Z =E/I
• Wenn Widerstände und Induktivitäten in Parallelschaltungen (genau wie in Reihenschaltungen) zusammengemischt werden, hat die Gesamtimpedanz einen Phasenwinkel zwischen 0° und +90°. Der Strom der Schaltung hat einen Phasenwinkel zwischen 0° und -90°.
• Parallel-Wechselstromkreise weisen dieselben grundlegenden Eigenschaften auf wie parallele Gleichstromkreise:Die Spannung ist im gesamten Stromkreis gleichmäßig, Zweigströme addieren sich zum Gesamtstrom und Impedanzen nehmen (durch die Kehrwertformel) ab, um die Gesamtimpedanz zu bilden.

VERWANDTE ARBEITSBLÄTTER:

• Induktoren-Arbeitsblatt