Resonanz in seriell-parallelen Schaltungen
In einfachen Blindschaltkreisen mit geringem oder keinem Widerstand zeigen sich die Auswirkungen einer radikal veränderten Impedanz bei der Resonanzfrequenz, die durch die zuvor gegebene Gleichung vorhergesagt wird. In einem parallelen (Tank) LC-Kreis bedeutet dies eine unendliche Impedanz bei Resonanz. In einer LC-Reihenschaltung bedeutet dies eine Impedanz von Null bei Resonanz:
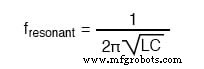
Sobald jedoch in den meisten LC-Schaltungen erhebliche Widerstandswerte eingeführt werden, wird diese einfache Resonanzberechnung ungültig.
Auf dieser Seite werfen wir einen Blick auf mehrere LC-Schaltungen mit zusätzlichem Widerstand, wobei die gleichen Werte für Kapazität und Induktivität wie zuvor verwendet werden:10 µF bzw. 100 mH.
Berechnung der Resonanzfrequenz eines hochohmigen Schaltkreises
Nach unserer einfachen Gleichung oben sollte die Resonanzfrequenz 159,155 Hz betragen. Beobachten Sie jedoch, wo der Strom in den folgenden SPICE-Analysen ein Maximum oder ein Minimum erreicht:
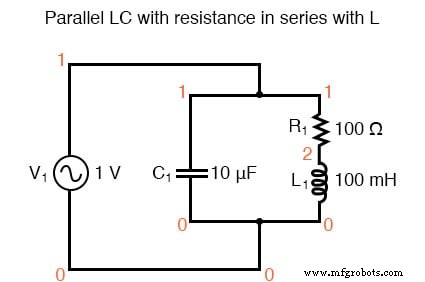
Parallel-LC-Schaltung mit Widerstand in Reihe mit L.
Ergebnisse:
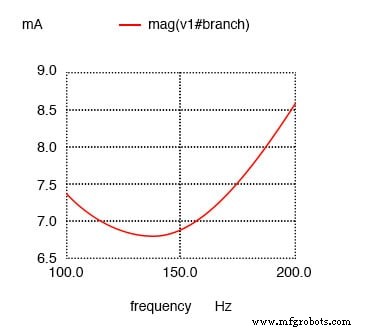
Widerstand in Reihe mit L erzeugt minimalen Strom bei 136,8 Hz statt berechneten 159,2 Hz
Mindeststrom bei 136,8 Hz statt 159,2 Hz!
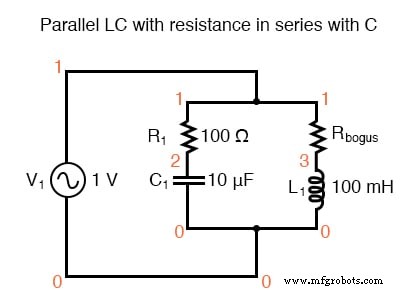
Parallel LC mit Widerstand in Reihe mit C.
Hier ist ein zusätzlicher Widerstand (Rbogus) erforderlich, um zu verhindern, dass SPICE bei der Analyse auf Probleme stößt. SPICE kann keinen Induktor handhaben, der direkt parallel zu einer Spannungsquelle oder einem anderen Induktor geschaltet ist, daher ist das Hinzufügen eines Vorwiderstands erforderlich, um die sonst gebildete Spannungsquelle/Induktorschleife „aufzubrechen“.
Dieser Widerstand ist als sehr ausgewählt niedriger Wert für minimalen Einfluss auf das Verhalten der Schaltung.
Mindeststrom bei ca. 180 Hz statt 159,2 Hz!
Ergebnisse:
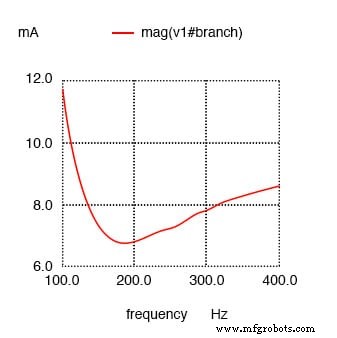
Widerstand in Reihe mit C verschiebt den minimalen Strom von berechneten 159,2 Hz auf ungefähr 180 Hz.
LC-Schaltungen der Serie
Wir richten unsere Aufmerksamkeit auf LC-Reihenschaltungen und experimentieren damit, signifikante Widerstände parallel zu L oder C zu platzieren. In den folgenden Reihenschaltungsbeispielen wird ein 1-Ω-Widerstand (R1) in Reihe mit der Induktivität und dem Kondensator geschaltet, um den Gesamtstrom bei . zu begrenzen Resonanz.
Der „zusätzliche“ Widerstand, der eingefügt wird, um Resonanzfrequenzeffekte zu beeinflussen, ist der 100--Widerstand R2. Die Ergebnisse sind in der folgenden Abbildung dargestellt.
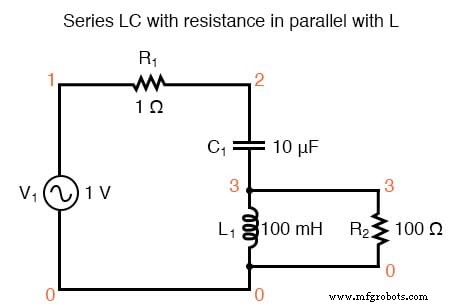
Serie LC-Schwingkreis mit Widerstand parallel zu L.
Maximaler Strom bei ca. 178,9 Hz statt 159,2 Hz!
Ergebnisse:
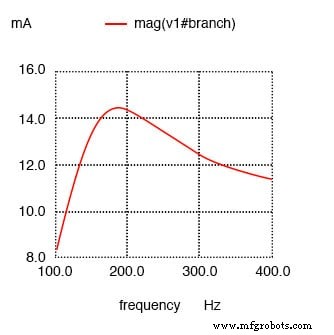
Reihenschwingkreis mit Widerstand parallel zu L verschiebt den maximalen Strom von 159,2 Hz auf ungefähr 180 Hz.
Und schließlich eine LC-Reihenschaltung mit dem signifikanten Widerstand parallel zum Kondensator. Die verschobene Resonanz ist unten gezeigt.
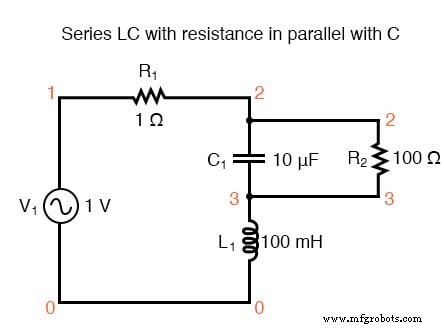
Serien-LC-Schwingkreis mit Widerstand parallel zu C.
Maximaler Strom bei 136,8 Hz statt 159,2 Hz!
Ergebnisse:
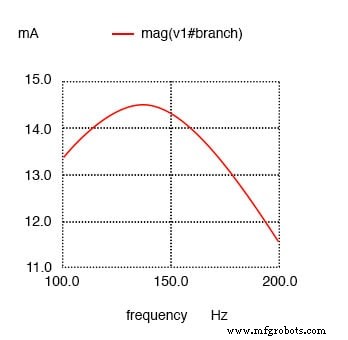
Widerstand parallel zu C im Serienresonanzkreis verschiebt das Strommaximum von berechneten 159,2 Hz auf etwa 136,8 Hz.
Antiresonanz in LC-Schaltungen
Die Tendenz des zusätzlichen Widerstands, den Punkt zu verzerren, an dem die Impedanz in einem LC-Kreis ein Maximum oder Minimum erreicht, wird als Antiresonanz bezeichnet . Der aufmerksame Beobachter wird ein Muster zwischen den vier oben aufgeführten SPICE-Beispielen bemerken, in Bezug darauf, wie sich der Widerstand auf die Resonanzspitze einer Schaltung auswirkt:
Parallel ("Tank") LC-Schaltung:
- R in Reihe mit L:Resonanzfrequenz nach unten verschoben
- R in Reihe mit C:Resonanzfrequenz nach oben shift verschoben
Serie LC-Schaltung:
- R parallel zu L:Resonanzfrequenz nach oben . verschoben
- R parallel zu C:Resonanzfrequenz nach unten verschoben
Auch dies veranschaulicht die komplementäre Natur von Kondensatoren und Induktivitäten:wie ein Widerstand in Reihe mit einem einen Antiresonanzeffekt erzeugt, der dem Widerstand parallel zum anderen entspricht. Wenn Sie sich die vier angegebenen SPICE-Beispiele noch genauer ansehen, werden Sie feststellen, dass die Frequenzen um den gleichen Betrag verschoben sind , und dass die Form der komplementären Graphen spiegelbildlich zueinander ist!
Antiresonanz ist ein Effekt, dem Resonanzkreisdesigner bewusst sein müssen. Die Gleichungen zur Bestimmung der Antiresonanz-„Verschiebung“ sind komplex und werden in dieser kurzen Lektion nicht behandelt. Es sollte dem Anfänger der Elektronik genügen, um zu verstehen, dass der Effekt existiert und was seine allgemeinen Tendenzen sind.
Der Skin-Effekt
Ein zusätzlicher Widerstand in einem LC-Kreis ist keine akademische Angelegenheit. Während es möglich ist, Kondensatoren mit vernachlässigbaren unerwünschten Widerständen herzustellen, sind Induktoren aufgrund der langen Drahtlängen, die bei ihrer Konstruktion verwendet werden, typischerweise mit erheblichen Widerständen geplagt.
Darüber hinaus neigt der Widerstand von Drähten dazu, mit steigender Frequenz zuzunehmen, aufgrund eines seltsamen Phänomens, das als . bekannt ist Hauteffekt wo Wechselstrom dazu neigt, durch die Mitte eines Drahtes zu fließen, wodurch die effektive Querschnittsfläche des Drahtes verringert wird.
Induktivitäten haben also nicht nur einen Widerstand, sondern einen sich ändernden, frequenzabhängigen Widerstand dazu.
Widerstand in Schaltkreisen hinzugefügt
Als ob der Widerstand des Drahtes einer Induktivität nicht ausreicht, um Probleme zu verursachen, müssen wir uns auch mit den „Kernverlusten“ von Eisenkern-Induktivitäten auseinandersetzen, die sich als zusätzlicher Widerstand im Stromkreis äußern.
Da Eisen sowohl ein elektrischer Leiter als auch ein Leiter des magnetischen Flusses ist, führt eine Änderung des Flusses, der durch den Wechselstrom durch die Spule erzeugt wird, dazu, im Kern selbst elektrische Ströme zu induzieren (Wirbelströme ).
Dieser Effekt kann man sich vorstellen, als ob der Eisenkern des Transformators eine Art sekundäre Transformatorspule wäre, die eine ohmsche Last speist:die nicht perfekte Leitfähigkeit des Eisenmetalls. Diese Effekte lassen sich mit Blechpaketen, gutem Kerndesign, hochwertigen Materialien minimieren, aber nie ganz eliminieren.
RLC-Schaltungen
Eine bemerkenswerte Ausnahme von der Regel des Schaltungswiderstands, der eine Resonanzfrequenzverschiebung verursacht, ist der Fall von Reihenwiderstand-Induktor-Kondensator-Schaltungen ("RLC"). Solange alle Komponenten in Reihe geschaltet sind, wird die Resonanzfrequenz des Stromkreises durch den Widerstand nicht beeinflusst. Das resultierende Diagramm ist unten gezeigt.
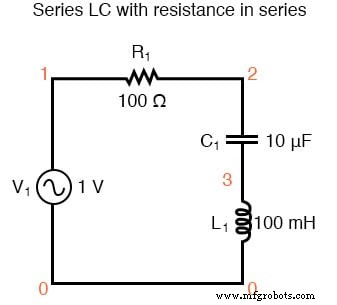
Serie LC mit Widerstand in Serie.
serie rlc schaltung v1 1 0 ac 1 sin r1 1 2 100 c1 2 3 10u l1 3 0 100m .ac lin 20 100 200 .plot ac i(v1) .Ende
Maximalstrom wieder bei 159,2 Hz!
Ergebnisse:
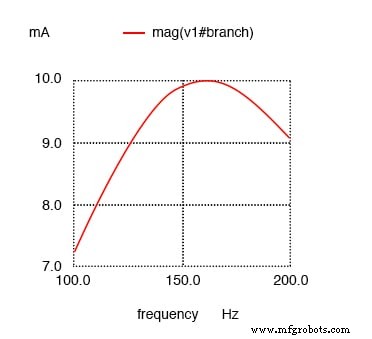
Der Widerstand im Serienresonanzkreis belässt das Strommaximum bei berechneten 159,2 Hz, was die Kurve verbreitert.
Beachten Sie, dass sich die Spitze des Stromdiagramms gegenüber der früheren LC-Serienschaltung (der mit dem 1--Token-Widerstand darin) nicht geändert hat, obwohl der Widerstand jetzt 100-mal größer ist. Das einzige, was sich geändert hat, ist die „Schärfe“ der Kurve.
Offensichtlich schwingt diese Schaltung nicht so stark wie eine mit weniger Serienwiderstand (man sagt, sie sei "weniger selektiv"), aber sie hat immerhin die gleiche Eigenfrequenz!
Dämpfende Wirkung von Antiresonanz
Bemerkenswert ist, dass die Antiresonanz die Schwingungen von freilaufenden LC-Kreisen wie Tankkreisen dämpft. Am Anfang dieses Kapitels haben wir gesehen, wie ein Kondensator und eine Induktivität, die direkt miteinander verbunden sind, sich wie ein Pendel verhalten und Spannungs- und Stromspitzen austauschen, genau wie ein Pendel kinetische und potenzielle Energie austauscht.
In einem perfekten Schwingkreis (kein Widerstand) würde diese Schwingung ewig andauern, so wie ein reibungsfreies Pendel für immer mit seiner Resonanzfrequenz schwingen würde. Aber reibungslose Maschinen sind in der realen Welt schwer zu finden, ebenso wie verlustfreie Tankkreise.
Energieverluste durch Widerstände (oder Induktorkernverluste oder abgestrahlte elektromagnetische Wellen oder ...) in einem Schwingkreis führen dazu, dass die Schwingungen in der Amplitude abklingen, bis sie nicht mehr vorhanden sind. Wenn in einem Tankkreis genügend Energieverluste vorhanden sind, wird er überhaupt nicht mitschwingen.
Die dämpfende Wirkung von Antiresonanz ist mehr als nur eine Kuriosität:Sie kann sehr effektiv genutzt werden, um unerwünschte zu beseitigen Schwingungen in Schaltungen mit Streuinduktivitäten und/oder Kapazitäten, wie dies bei fast allen Schaltungen der Fall ist. Beachten Sie die folgende L/R-Zeitverzögerungsschaltung:(Abbildung unten)
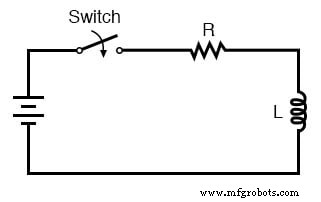
L/R-Zeitverzögerungsschaltung
Die Idee dieser Schaltung ist einfach:den Induktor zu „laden“, wenn der Schalter geschlossen ist. Die Ladegeschwindigkeit des Induktors wird durch das Verhältnis L/R eingestellt, das die Zeitkonstante der Schaltung in Sekunden ist.
Wenn Sie jedoch eine solche Schaltung aufbauen, können Sie beim Schließen des Schalters unerwartete Spannungsschwankungen (AC) an der Induktivität feststellen. (Abbildung unten) Warum ist das so? Es gibt keinen Kondensator in der Schaltung, wie können wir also mit nur einer Induktivität, einem Widerstand und einer Batterie Resonanzschwingungen erzeugen?
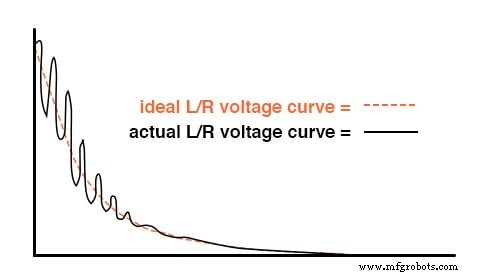
Induktor-Klingeln aufgrund von Resonanz mit Streukapazität.
Alle Induktoren enthalten eine gewisse Streukapazität aufgrund von Windungs-zu-Windungs- und Windungs-zu-Ader-Isolationsstrecken. Außerdem kann die Anordnung von Leitern der Schaltung Streukapazität erzeugen. Während ein sauberes Schaltungslayout wichtig ist, um einen Großteil dieser Streukapazitäten zu eliminieren, wird es immer einige geben, die Sie nicht eliminieren können.
Wenn dies Resonanzprobleme (unerwünschte Wechselstromschwingungen) verursacht, kann ein zusätzlicher Widerstand eine Möglichkeit sein, dem entgegenzuwirken. Wenn der Widerstand R groß genug ist, verursacht er einen Zustand der Antiresonanz, der genügend Energie abgibt, um zu verhindern, dass die Induktivität und die Streukapazität sehr lange Schwingungen aufrechterhalten.
Interessanterweise wird das Prinzip des Widerstands zur Eliminierung unerwünschter Resonanzen häufig bei der Konstruktion mechanischer Systeme verwendet, bei denen jedes sich bewegende Objekt mit Masse ein potenzieller Resonator ist.
Eine sehr verbreitete Anwendung hierfür ist der Einsatz von Stoßdämpfern in Automobilen. Ohne Stoßdämpfer würden Autos mit ihrer Resonanzfrequenz wild aufprallen, wenn sie auf jede Bodenwelle prallen. Die Aufgabe des Stoßdämpfers besteht darin, einen starken Antiresonanzeffekt zu erzeugen, indem er Energie hydraulisch ableitet (so wie ein Widerstand Energie elektrisch ableitet).
RÜCKBLICK:
- Zusätzlicher Widerstand zu einem LC-Kreis kann einen Zustand verursachen, der als Antiresonanz bekannt ist , wo die Spitzenimpedanzeffekte bei anderen Frequenzen auftreten als denen, die gleiche kapazitive und induktive Reaktanzen ergeben.
- Ein Widerstand, der realen Induktivitäten innewohnt, kann stark zu den Bedingungen der Antiresonanz beitragen. Eine Quelle solcher Resistenzen ist der Hauteffekt , verursacht durch den Ausschluss von Wechselstrom aus der Mitte der Leiter. Eine andere Quelle sind die Kernverluste in Induktivitäten mit Eisenkern.
- In einer einfachen LC-Reihenschaltung mit Widerstand (einer „RLC“-Schaltung) ist der Widerstand nicht Antiresonanz erzeugen. Resonanz tritt immer noch auf, wenn kapazitive und induktive Reaktanzen gleich sind.
VERWANDTE ARBEITSBLÄTTER:
- Resonanz-Arbeitsblatt
Industrietechnik
- AC-Schaltungsgleichungen
- Motorsteuerkreise
- Verwenden mehrerer Kombinationsstrecken
- Verstärkerschaltungen
- Was sind Stromkreise?
- Computersimulation elektrischer Schaltungen
- Was sind „Serien“- und „Parallel“-Schaltungen?
- Einfache Serienschaltungen
- Aufbau einfacher Widerstandsschaltungen
- Eine Einführung in verschiedene Hydraulikkreisläufe



